spike可以定义为一维、 二维或者三维数据内相邻小区域的异常值。 中值滤波器是以当前数据点为中心的小窗口的中值来代替每个数据点, 其原理可以用来剔除这些异常值, 但是非spike的信号也将随着滤波操作而失真。 因此, 我们开发了一种分两步进行的spike剔除方法, 第一步是定位spike, 第二步是只对被定位的spike执行中值滤波。 这种策略可以较好地去除spike, 并保留原始信号的高保真度。 定位spike是其中的关键, 可以根据中值滤波后的数据和原始数据作偏差, 通过设置阈值来识别spike。 将原始数据表示为M, 滤波后的数据表示为N, 偏差表示为E(E=M-N)。 E的分布可以近似表示为高斯函数[式(1)]

f(x)=12πσexp-(x-μ)22σ2(1)

式(1)中, x是随机变量, f(x)是概率密度, μ 是期望, σ 是标准差。

根据3-σ 规则, 99.7%的数据在以期望μ 为中心, 标准方差σ 的3倍区域内。 这个特征可以用来识别spike, 因为spike通常稀疏地分布在测量数据中, 并且具有比正常信号高得多的强度。 这些spike可以通过根据E的分布性质设置一个阈值来识别。 该阈值将把E中大部分较小的数据点识别为正常值, 而当E中的一个数据点的值超过该阈值时, 它将被识别为spike。 如果原始数据M中没有spike, 则E中的大部分值将非常小, 拟合分布的期望将接近0。 但如果spike存在, 使用式(1)直接拟合, 拟合曲线将因为异常值的原因偏离它的真实分布。 为解决这个问题, 本文按升序排序E, 并使用中间数据而不是使用E中的所有值来拟合分布。 我们使用分位数方法将E切成一个系列连续区域。 分位数的函数可以被描述为式(2)

τ=P(X≤xτ)=F(xτ)(2)

式(2)中, X是随机变量, F(x)是连续分布函数, P是概率, τ 是分位数。 分位数指满足条件P(X< x_τ )的点。

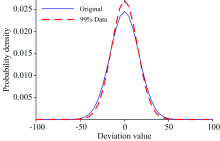
根据分位数的概念将E中的数据点以概率的方式划分为100个份, 通过选择合适的τ , 取中间的99个部分作为拟合分布所用的数据, 中间99%的数据已剔除强度很大的spike和测量结果为负的CCD坏点, 可以表现真实拉曼信号特征, 经过实验测试, 取99%以上的中间数据会引入个别异常值, 取99%以下的数据, 对拟合的分布提升不明显, 且可能会丢失一些真实信号。 原始数据和经过排序后的中间99%数据的拟合分布结果如图1所示。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 原始数据和中间99%的数据的分布Fig.1 The distribution with the original data and middle 99% data

图1是使用全部数据及中间99%的数据做拟合的概率密度函数图, 其中使用99%的数据的分布更瘦更高, 意义为数据更加集中, 异常值和正常值的距离更远, 且大部分的偏差E在0左右, 99%的数据拟合后左右两端比使用全部数据的拟合更窄, 意味着正常值的数据更加集中, 阈值的设置更加简单。

通过基于概率密度函数(PDF)的原理, 为E的真实分布设置一个阈值, 可以很容易地识别spike。 该原理可以表示为式(3)

P(X≤x)=FX(x)=∫-∞xf(t)dt(3)

式(3)中, X是随机变量, x是实数, P为概率, f(t)为概率密度函数。

PDF函数可以通过设定一个数来获取数据超过该数的概率, 但由这种直接方法设置的阈值将有两个缺陷。 一是阈值选择的难度: 关于spike和正常值之间的距离尚不清楚, 因此没有参考依据。 另一个缺陷是缺乏自动化和通用性: 针对不同的拉曼数据需要设置不同的阈值, 这对分析者来说很不方便且设置的值与使用者的经验有关。 为了解决这些问题, 我们采用基于逆累积分布函数(ICDF)的反向思想来直接设置概率阈值, 通过设定某个概率P(X≥ x), 可以根据该分布函数自动确定一个阈值x, 数据超过该值为满足这个概率(X≥ x)。 因此, 在不同的拉曼数据中将根据概率自动调整不同的绝对阈值x以剔除spike。 为了方便起见, 本文以下部分中设置的阈值指的均是概率阈值P。

在通过阈值设置检测到spike之后, 下一步是用表示真实拉曼特征的值来替换原始数据M中的spike。 最简单、 直接的方法是用线性插值来填充空位置。 但这种方法引入了伪影, 并会因拉曼数据的复杂性而导致错误的结果。 应用非线性函数进行插值可以使替换完成的拉曼数据更逼近真实数据。 然而, 一些非线性函数会引入更多的变量和未知的参数, 这将使这个过程变得极其复杂, 错误的参数甚至会降低拉曼特征的准确性。 一种简单有效的方法是使用中值滤波后的数据N中的值代替原始数据M中的spike。 中值将当前像素中的信号与前后像素连接起来, 确保该值的可靠性。 此外, 它仅需要少量的参数来确定, 易于操作。

整个算法的基本思想是在偏差分布E中找到超过阈值的数据点, 并将其标记为spike。 然后去除原始数据M中的这些spike, 并填充对应位置的滤波后的N值, 具体步骤如表1所示。 拉曼数据M可以是一维拉曼光谱、 二维拉曼图像和三维拉曼数据立方体, 取决于维度D。 Median(M, W)表示对数据M应用窗口大小为W的中值滤波器, Fit(E)代表对分布E作曲线拟合, M(I)是数据M在位置I的索引值, I可以是(i), 表示一维数据, (i, j)表示二维数据, (i, j, k)表示三维数据。

表1

Table 1

表1(Table 1)

表1 算法流程图 Table 1 Flowchart of algorithm Input raw Raman data M, Window size W, Threshold θ , Dimension D; 1 Data N=Median(M, W); 2 Deviation E=M-N; 3 Distribution F=Fit(middle 99% E); 4 Value V1=F(θ ), V2=F(1-θ ); 5 If E(I)< V1 or E(I)> V2 6 Replace M(I) by N(I); 7 Endif Output Data M

表1 算法流程图 Table 1 Flowchart of algorithm

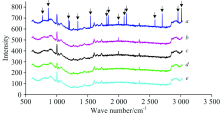
参数优化包括中值滤波器的窗口大小的选择和阈值的设定。 这些参数应根据拉曼数据的噪声水平、 强度和锐度的差异来选择, 以在不影响真实拉曼特征的情况下准确地去除spike。 本文针对三种维度下不同窗口尺寸和不同阈值进行实验。 在此, 以一维拉曼谱为例, 演示如何选择合适的参数。 拉曼光谱中不同参数下的结果如图2所示。

图2

Fig.2

Figure Option ViewDownloadNew Window

图2 不同窗口尺寸和阈值的一维spike剔除 a: 原始拉曼光谱; b: 窗口尺寸为7, 阈值为1× 10-5的spike剔除过程; c: 窗口尺寸为3, 阈值为1× 10-5的spike剔除过程; d: 窗口尺寸为7, 阈值为1× 10-3的spike剔除过程; e: 窗口尺寸为3, 阈值为1× 10-3的spike剔除过程Fig.2 Spike removal of 1-dimensional spectra with different window size and threshold a: Raw spectrum; b: Spike removal with window size 7, threshold 1× 10-5; c: Spike removal with window size 3, threshold 1× 10-5; d: Spike removal with window size 7, threshold 1× 10-3; e: Spike removal with window size 3, threshold 1× 10-3. Arbitrary offsets were applied on the spectra for better visualization

图2a为未经spike剔除算法的一维拉曼光谱数据, 使用较大的窗口, 有可能无法完全剔除图中的spike(如图2b所示), 或对图中的真实拉曼峰造成影响(如图2d), 使用较小的窗口尺寸的结果如图2e所示, 由于spike窄带宽, 高强度特征, 小窗口识别更成功。 因此, 我们选择3作为一维拉曼光谱的窗口尺寸。

在实验中, 我们设置阈值1× 10^-3和1× 10^-5并进行比较。 尽管阈值相差两个数量级但只有一个位于2 000波数附近的spike没有被检测到。 引入分位数的方法确保了拟合分布是使用正常值, 扩大了正常值和spike的差异, 让阈值选择空间足够大。

二维拉曼图像和三维拉曼数据立方体的参数选择与上述操作相似。 对于二维图像, 将使用二维中值滤波器作用于原始数据。 从一维拉曼光谱到二维拉曼图像的扩展不仅仅是从行扩展到列的更改, 这涉及到滤波器在不同对象上的操作。 在一维数据中, 对不同波数下的信号强度进行滤波, 是光谱维度上的滤波。 在二维中, 同一波数上的不同像素信号被滤波, 对于采集过程, 属于空间上的滤波。 原始数据与中值滤波后的数据之间的偏差是二维分布, 因此设置的阈值也是二维数据, 对应于图像的行和列。 为了简化拟合分布, 我们首先将二维偏差数据重组为一维偏差数据。 对扩展的一维数据的分析与前面描述的一维拉曼光谱数据相同。 本文选择3× 3作为窗口大小, 1× 10^-6作为设定的阈值用来剔除二维拉曼图像中的spike。

对于三维拉曼数据立方体, 数据的中值滤波器和偏差也将是三维的。 三维数据的扩展既需要考虑拉曼数据采集的时间, 也需要考虑不同的波数, 首先是在深度方向上, 然后是在宽度方向上, 最后是在高度方向上。 这将极大增加数据的数量, 并使偏差分布更接近真实分布, 也更准确。

根据参数的选择, 对于三维数据立方体, 信号的变化受到多维的限制。 因此, 一个小的滤波窗口足以去除spike, 也可以减少程序的处理时间。 由于数据量的扩展, 阈值设置为1× 10^-6。

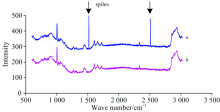
一维spike剔除的处理结果如图3所示。 Spike出现概率较小, 但是强度很大, 远超过其他波峰, 该算法很好地剔除了spike, 同时完整保留了1 000 cm^-1处的强拉曼峰(细胞成分: 苯丙氨酸)。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 一维拉曼光谱spike剔除 a: 原始拉曼光谱; b: 经过spike剔除算法后的拉曼光谱Fig.3 1-dimensional Raman spectra spike removal process a: Raw Raman spectrum; b: Raman Spectrum after 1-dimensional spike removal. Arbitrary offsets were applied on the spectra for better visualization

作为验证, 测试了20个光谱, 其中有10个手动添加的人工spike。 增加的spike位置是随机的, 强度为峰值的0.1~0.4倍。 实验结果见图4。

图4

Fig.4

Figure Option ViewDownloadNew Window

图4 一维拉曼光谱(加人工spike) (a): 经过spike剔除后的拉曼光谱; (b): 增加0.1倍人工spike的拉曼光谱; (c): 增加0.2倍人工spike的拉曼光谱; (d): 增加0.3倍人工spike的拉曼光谱; (e): 增加0.4倍人工spike的拉曼光谱; (f): 增加0.5倍人工spike的拉曼光谱Fig.4 1-dimensional spectrum with artificial spikes (a): Raman spectrum after spike removal; (b): Raman spectrum with 0.1 times artificial spikes; (c): Raman spectrum with 0.2 times artificial spikes; (d): Raman spectrum with 0.3 times artificial spikes; (e): Raman spectrum with 0.4 times artificial spikes; (f): Raman spectrum with 0.5 times artificial spikes

用该算法进行了10次独立的验证实验, 并将检测结果进行平均, 最终结果如表2所示。 其中Ratios表示峰值的比例(0.1~0.4倍), Predicted表示算法所预测出来的spike数目, True为真实spike数量, Percentage是算法的准确度。

表2

Table 2

表2(Table 2)

表2 一维拉曼光谱spike检测 Table 2 1-dimensional Raman spectra spike detection Ratios Predicted True Percentage/% 0.1 175 200 87.5 0.2 195 200 97.5 0.3 197 200 98.5 0.4 199 200 99.5

表2 一维拉曼光谱spike检测 Table 2 1-dimensional Raman spectra spike detection

实验结果所示, 在spike强度较低情况下(峰值的比值较低), spike剔除算法的性能较差, 因为人工spike可能由于其随机位置而落入信号的低处, 使得叠加的信号太小, 无法被检测到。 当该比率增加到40%时, 检测灵敏度可达到99.5%。 参考文献[15]的检测灵敏度为97.5%, 参考文献[19]中检测超过峰值50%的spike识别算法, 灵敏度可以达到99%, 与它们相比, 本文介绍的方法可以检测强度更弱的spike, 且灵敏度有较大提升。

图5(a)和(b)为波数在2 940 cm^-1的真实拉曼图像的二维spike剔除处理结果。 其中Y轴是线数, X轴是光谱条数, 构成100× 400的拉曼图像。 颜色代表相对值的大小, 蓝色代表小数值, 黄色代表高数值。 未剔除spike前, 高强度的spike使图像其他位置的特征对比度降低。 在剔除spike后, 严重污染的原始拉曼图像可以显示图像的特征。

图5

Fig.5

	Figure Option ViewDownloadNew Window
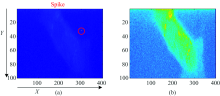	图5 二维拉曼图像spike剔除 (a): 原始拉曼图像; (b): 经过二维spike剔除算法处理后的拉曼图像Fig.5 2-dimensional Raman image spike removal process (a): Raw Raman image; (b): Raman image after 2-dimensional spike removal

对于二维验证实验, 我们从1 340张图像中随机选择20张, 并在每张图像中选择10个随机位置设置spike。 然后将每个选定位置的值设定为原本值加上当前图像最大像素值的0.1到0.3倍作为spike。

通过增加不同的比率, 我们得到了不同的检测结果。 为减少验证实验的随机误差, 进行了10个独立验证实验, 将检测结果进行平均, 最终结果如表3所示。

表3

Table 3

表3(Table 3)

表3 二维拉曼图像spike检测 Table 3 2-dimensional Raman image spike detection Ratios Predicted True Percentage/% 0.1 174 200 87 0.2 194 200 97 0.3 199 200 99.5

表3 二维拉曼图像spike检测 Table 3 2-dimensional Raman image spike detection

对于二维spike剔除方法, 当spike强度超过峰值的30%时, 可以有效地检测spike。 与参考文献[19]中的二维spike检测算法相比, 本文介绍的方法可以在spike强度较小的情况下检测和剔除spike。

二维spike检测灵敏度高于一维, 通过二维spike剔除方法可以去除具有较低强度的spike。

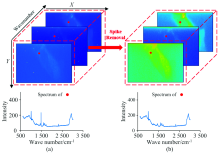
三维拉曼数据立方体包含三维坐标信息和当前位置的值, 它表示四维信息。 在图中难以表示四维信息。 因此, 在使用了三维spike剔除方法后, 我们可以简单地使用图6来显示三维拉曼数据立方体spike剔除的效果。

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 三维拉曼数据立方体spike剔除 (a): 原始拉曼数据立方体; (b): 经过三维spike剔除算法处理后的拉曼数据立方体Fig.6 3-dimensional Raman data cube spike removal process (a): Raw Raman data cube; (b): Raman data cube after 3-dimensional spike removal

拉曼数据立方体可以表示为1 340张二维拉曼图像, 或40 000条一维拉曼光谱。 因此, 用三维方法剔除spike后, 可以直接剔除一维和二维的spike。 图6中的立方体是指一个包含1 340个拉曼图像的真实样本数据立方体。 图像上的点表示某条拉曼光谱, 图的下部显示该光谱的spike剔除结果。 图中选取三个数据立方体切片作为效果说明, 分别对应波数在1 000, 2 130和2 880 cm^-1时的拉曼图像。

对于三维验证实验, 我们随机选择20个波数上的图像, 并在随机位置添加10个spike。 spike的强度是拉曼数据立方体最高值的0.1~0.2倍。 计算结果如表4所示。

表4

Table 4

表4(Table 4)

表4 三维拉曼数据立方体spike检测 Table 4 3-dimensional Raman data cube spike detection Ratios Predicted True Percentage/% 0.1 186 200 93 0.2 199 200 99.5

表4 三维拉曼数据立方体spike检测 Table 4 3-dimensional Raman data cube spike detection

当强度大于峰值的20%时, 可剔除所有spike。 与一维和二维spike剔除相比, 三维方法可以检测更低强度的spike, 提高数据处理能力。 这是一种新的针对大量拉曼数据的spike剔除方法, 在其他文献中很少被提及。

灵敏度随着维度的增加而增加有两个原因。 一方面, 数据的特征更加明显。 另一方面, 维数的增加使数据量迅速增加, 数据拟合出的分布更准确, spike剔除算法更灵敏。