引用本文
欧阳爱国, 林同征, 胡军, 余斌, 刘燕德. 激光诱导击穿光谱技术对高铁车轮硬度检测模型优化研究[J]. 光谱学与光谱分析, 2022,42(10): 3109-3115.
OUYANG Ai-guo, LIN Tong-zheng, HU Jun, YU Bin, LIU Yan-de. Optimization of Hardness Testing Model of High-Speed Iron Wheel by Laser-Induced Breakdown Spectroscopy[J]. Spectroscopy and Spectral Analysis, 2022,42(10): 3109-3115.
Doi:10.3964/j.issn.1000-0593(2022)10-3109-07  
Permissions
Copyright©2022, 《光谱学与光谱分析》期刊社
《光谱学与光谱分析》期刊社 所有
激光诱导击穿光谱技术对高铁车轮硬度检测模型优化研究
欧阳爱国, 林同征, 胡军, 余斌, 刘燕德
华东交通大学机电与车辆工程学院, 江西 南昌 330013

作者简介: 欧阳爱国, 1968年生, 华东交通大学机电与车辆工程学院教授 e-mail: ouyang1968711@163.com

收稿日期: 2021-08-10 修回日期: 2022-03-05 接受日期: 2022-03-05
基金: 国家自然科学基金项目(31760344), 水果光电检测技术能力提升项目(S2016-90), 江西省教育厅科学技术研究项目(GJJ60516), 江西省优势科技创新团队建设计划项目(20153BCB24002), 南方山地果园智能化管理技术与装备协同创新中心(赣教高字[2014]60号)资助
摘要

我国铁路跨度长、 运营时间长、 运行环境变化较大, 故对于车轮的磨损较大, 为保障高速铁路的安全运行, 高速列车车轮表面硬度就成为了一项重要参考指标。 激光诱导击穿光谱(LIBS)实验平台对8块不同硬度的HS7高铁车轮用钢样品进行击穿获取LIBS光谱数据, 发现基体元素(Fe)和合金元素(Cr, Mo, W)的谱线强度、 离子与原子线的强度比值(Ⅱ/Ⅰ)以及合金元素谱线强度与基体元素谱线强度的强度比值( A/M), 分别与样品硬度有着不同程度的相关关系。 利用此相关关系分别建立了以谱线强度和谱线强度结合谱线强度比值为变量的偏最小二乘法(PLS)定量分析模型, 在建立模型前采用标准正态变量变换(SNV)、 Savitzky-Golay卷积二阶导和高斯滤波(Gaussian filter)三种预处理方法来减小实验误差。 结果表明, 以谱线强度为变量的模型中采用SNV预处理后建立的PLS模型效果最佳, 校正集的确定系数为0.98, 均方根误差为1.30, 预测集的确定系数为0.90, 均方根误差为2.43; 以谱线强度结合谱线强度比值为变量的模型中采用原始数据建立的PLS模型效果最佳, 校正集的确定系数为0.99, 均方根误差为0.79, 预测集的确定系数为0.94, 均方根误差为2.44, 且通过对比发现以谱线强度结合谱线强度比值为变量的模型其预测精确度及其稳定性相比于以谱线强度为变量的模型均有所提升。 该结果表明, 利用谱线强度和离子与原子线的强度比、 合金元素谱线强度与基体元素谱线强度的强度比相结合的结果作为模型变量, 能显著提升PLS模型对于金属材料表面硬度预测的能力, 可以构建一种相关性更强的定量分析模型。 研究表明, 采用激光诱导击穿光谱技术结合偏最小二乘法定量分析高铁车轮硬度具有一定可行性, 可将该技术应用于现场诊断、 估算高速列车车轮表面硬度, 为维持高速列车安全运行提供一定的保障。

关键词: 激光诱导击穿光谱; 高速列车车轮表面硬度; 谱线强度; 偏最小二乘法
中图分类号:O657.3 文献标志码:A
Optimization of Hardness Testing Model of High-Speed Iron Wheel by Laser-Induced Breakdown Spectroscopy
OUYANG Ai-guo, LIN Tong-zheng, HU Jun, YU Bin, LIU Yan-de
School of Mechanotronics and Vehicle Engineering, East China Jiaotong University, Nanchang 330013, China
Abstract

China's railway has a long span, long operation time and great changes in operation environment, so the wear of wheels is large. In order to ensure the safe operation of high-speed railways, the surface hardness of high-speed train wheels has become an important parameter. The laser-induced breakdown spectroscopy (LIBS) experimental platform was used to conduct the breakdown of eight HS7 high-speed rail wheel steel samples with a different hardness to obtain the LIBS spectral data. It was found that the spectral intensity of matrix elements (Fe) and alloy elements (Cr, Mo, W), the intensity ratio of ion line to atomic line (Ⅱ/Ⅰ), and the spectral intensity ratio of alloy elements to matrix elements( A/M) had different degrees of correlation with the hardness of the samples. Partial least squares (PLS) quantitative analysis model with spectral line intensity and spectral line intensity combined with spectral line intensity ratio as variables was established. Before the establishment of the model, three preprocessing methods, standard normal variable transformation (SNV), Savitzky-Golay convolution second derivative and Gaussian filter (Gaussian filter), were used to reduce the experimental error. The results show that the PLS model established by SNV pretreatment is the best in the model with spectral line intensity as a variable. The determination coefficient of the calibration set is 0.98, the root mean square error is 1.30, the determination coefficient of the prediction set is 0.90, and the root means square error is 2.43. The PLS model established with the original data has the best effect in the model with the ratio of spectral line intensity to spectral line intensity as the variable. The determination coefficient of the calibration set is 0.99, the root mean square error is 0.79, the determination coefficient of the prediction set is 0.94, and the root means square error is 2.44. Through comparison, it is found that the prediction accuracy and stability of the model with the ratio of spectral line intensity to spectral line intensity as the variable are improved compared with the model with the spectral line intensity as the variable. The results show the combined results of spectral line intensity and the intensity ratio of ions to atomic lines. Moreover, the spectral line intensity ratio of alloy elements to matrix elements is used as model variables, which can significantly improve the solution of the PLS model for the prediction of surface hardness of metal materials and construct a quantitative analysis model with stronger correlation. Studies have shown that it is feasible to quantitatively analyze the hardness of high-speed railway wheels by using laser-induced breakdown spectroscopy combined with the partial least squares method. This technology can be applied to the field diagnosis and estimation of the surface hardness of high-speed train wheels, guaranteeing the safe operation of high-speed trains.

Keyword: Laser-induced breakdown spectroscopy; Surface hardness of high speed train wheels; Spectral line intensity; Partial least squares
引言

随着我国高速铁路的快速发展, 轮轨变形、 疲劳损伤接连出现, 已经严重的影响铁路运行的安全和服役可靠性, 而高速列车运行安全和服役可靠性是高铁研究与运营过程中最为关注的重点[1]。 列车的牵引运行、 制动减速都依靠车轮摩擦副提供的牵引力和制动力来实现, 故车轮的接触面上有着复杂的多轴交变应力, 其中包含接触应力、 弯曲应力和切应力等, 对车轮的硬度和耐磨性提出了严格的要求[2, 3]。 因此对高铁车轮硬度的检测研究是维持高速列车安全运行的一个重要研究课题。

激光诱导击穿光谱(laser-induced breakdown spectroscopy, LIBS)技术是一门原子光谱分析技术, 正在快速的发展, 它利用高能脉冲激光将样品表面微观物质激发到等离子体状态, 并分析产生的元素发射光谱[4, 5], 具有实时在线[6]、 远距离遥控[7]、 无复杂的样品制备过程[8, 9]、 接近无损分析等优点。 2018年黄健伟等[10]分析了发射线强度与硬度的关系, 构建了钢材表面硬度的标定模型, 其结果表明采用化学计量学对LIBS光谱进行分析的方法, 可以作为一种钢的力学性能评估方法。 2020年贾皓月等[11]研究了D2钢硬度与Fe的离子和原子光谱强度比的关系, 同时也研究了D2钢硬度与等离子体温度的关系, 实验结果表明LIBS技术可以很好的表征钢材硬度特性。

目前, LIBS在金属材料的硬度特性检测方面应用尚较少, 为了促进这一重要课题的发展, 提出了基于LIBS的高速车轮硬度预测模型, 可将其应用于现场检测, 相对于目前的高铁车轮硬度检测技术具有明显的优势。

1 实验部分
1.1 样品制备

HS7钢是一种含碳量高的钨钼系含钴高速工具钢, 不仅硬度高、 耐热性较好, 且机械加工性能好、 具备一定的耐磨性, 目前被确定为我国时速300 km以上的高铁车轮用钢。 样品是直径20 mm厚度10 mm的8块圆柱体, 是由相同热处理得出的不同硬度的HS7钢。 利用日本日立公司生产的场发射扫描电镜(scanning electron microscope, SEM)SU8010中的EDS(Energy Dispersive Spectrometer)能谱分析技术对8块样品进行线扫描测试, 并将测取的化学成分取平均值, 如表1所示。

表1 HS7钢主要化学成分含量(质量分数, %) Table 1 Main chemical components of HS7 steel (Wt%)

将样品表面放置于MP-2DE金相试样磨抛机上用砂纸从200目到2 000目进行约400目的梯度打磨, 再用直径3.5 mm的钻石抛光膏将其抛光至镜面, 用无水乙醇清洗后采用Qness 10A高精度显微硬度测试仪测量样品的维氏硬度。 采用负载为200 gf, 加载时间为10 s的力, 对样品随机取5个测试点, 测试点如图1所示。 最终, 显微硬度值为5个点硬度的平均值, 如表2所示。

图1 采用Qness 10A高精度显微硬度测试仪硬度检测点Fig.1 Hardness detection points using QNESS 10A high-precision micro-hardness tester

表2 样品的维氏硬度测量值 Table 2 Measured vickers hardness values of the samples

由于硬度检测后样品表面有一定损伤痕迹, 故在进行LIBS实验前采用MP-2DE金相试样磨抛机重复上述制样过程, 将样品表面恢复至镜面。 然后用无水乙醇将样品抛磨位置洗净, 这样就能保证该样品的平整性, 减少由于激光焦深变化而引起的电位波动, 并且可以降低激光诱导等离子体信号中因表面氧化层和外来污染物对LIBS测量造成的影响。

1.2 LIBS设备及参数

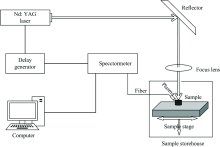
实验所使用的设备为海洋光学MX2500+, 激光器为quantel CFR200系列激光器, LIBS系统原理图如图2所示。 由Q开关Nd:YAG激光器激发出激光, 含有较高能量的激光脉冲宽度为纳秒量级, 经45° 平面发射镜反射后, 被透镜聚焦至样品表面, 灼烧剥离其上微量物质形成等离子体。 光纤位于样品上方, 其功能是采集灼烧样品表面过程中形成的等离子体光谱信号, 并将其传输至光谱仪, 然后利用其配套软件MaxLIBS对参数进行设置, 并控制对元素波长及信号强度的采集。

图2 LIBS系统原理图Fig.2 Schematic diagram of LIBS system

实验参数如下: 激光能量设为50 mJ, 光谱仪采集的波长范围为198.71~727.69 nm, 光学分辨率为0.1 nm, 积分时间设置为光谱仪采集信号的最小宽度1 ms。 根据最佳信噪比, 选择延迟时间为2 500 ns。 考虑到试样组成的不均匀性和激光作用位置改变时激光能量的不稳定性, 设计并实现了4× 4矩阵位置(每个位置利用激光脉冲烧蚀200次)的专用测量方案, 相邻两检测点间距≈ 0.6mm两两之间互不影响, 这样每个样品中含有相互独立的16个样本, 共计128个独立样本。

1.3 数据处理

由于坑道效应, 即随着激光脉冲烧蚀样品次数的增加而导致激光烧蚀坑的深度和形状发生变化, 影响了后续过程中激光对样品的烧蚀和所获取的谱线强度[12]。 故为了样品表面变化对激光烧蚀样品过程不产生较大的影响, 将所有样品测量点的前30个光谱数据进行剔除, 后文中的谱线强度均为测量点第31到第200次所获光谱数据求取的平均值。

为降低激光能量的波动、 检测环境的干扰及样品不均匀等原因的影响, 建模前对数据进行三种不同的预处理, 分别为标准正态变量变换(standard normal variate transformation, SNV)、 Savitzky-Golay卷积二阶导和高斯滤波(Gaussian filter)。

偏最小二乘法(partial least squares, PLS)是一种对多元因子进行回归统计的方法, 能将光谱数据中所含信息进行提取分析, 并被大量应用于构建拥有高度共线性变量的线性模型中, 该方法能够建立变量与少量样本之间的关系[13]。 其模型可表示为:

Y=bX+e(1)

式(1)中: b为回归系数; e为残差矩阵。

在PLS模型构建过程中, 潜变量(latent variables, LVs)的确定也较为重要, 一般采用交叉验证的方法确定LVs或者直接取内部校正集预测误差最小时的LVs为最佳值。

2 结果与讨论
2.1 光谱特性分析

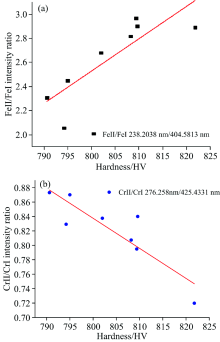
利用激光击打在物质表面与其相互作用可产生等离子体的原理, LIBS技术可采集激光烧蚀材料所激发等离子体火花的特征光谱线, 用以检测元素含量、 材料硬度和纯度等物理特性[14]。 为了对不同硬度样品与样品的光谱特性差异进行分析, 实验探究了样品硬度与样品基体元素(Fe)、 合金元素(Cr, Mo, W)的LIBS谱线强度、 离子与原子线的LIBS强度比值(Ⅱ /Ⅰ )以及合金元素谱线强度与基体元素谱线强度的强度比值(A/M)之间的关系, 并分别与样品硬度之间建立了关系。 如图3所示, Fe, Cr和Mo元素的谱线强度与样品硬度存在不同程度上的正相关关系, W元素的谱线强度与样品硬度存在一定程度上的负相关关系。 这是由于不同元素的激发特性和自吸收效应不同, 所以光谱强度的斜率不同。 根据各元素的化学性质、 激发电位、 电离程度以及光谱强度, 选择以下谱线: Fe Ⅰ 358.119 3 nm, 404.581 3 nm, Fe Ⅱ 238.203 8 nm, Cr Ⅰ 425.433 1 nm, Cr Ⅱ 276.258 nm, Mo Ⅰ 313.259 4 nm和W Ⅰ 283.138 nm进行离子线与原子线的强度比值、 合金元素与基体元素的谱线强度比值与样品硬度之间关系的研究。 如图4(a)所示, Fe Ⅱ 238.203 8 nm和Fe Ⅰ 404.581 3 nm的比值与样品硬度在一定程度上存在正相关关系, 但由图4(b)可以看出Cr Ⅱ 276.25 8 nm和Cr Ⅰ 425.433 1 nm的比值与样品硬度存在一定的负相关关系。 这个结果表明离子与原子线的强度比可一定程度上表现样品的基体特征。 如图5所示, Mo Ⅰ 313.259 4 nm和Fe Ⅰ 358.119 3 nm, W Ⅰ 283.138 nm和Fe Ⅰ 358.119 3 nm的强度比值与样品硬度均在一定程度上存在正相关关系, 这个结果表明激光作用于不同基体特征对象时所产生的基体效应有所不同, 同时也说明合金元素与基体元素的谱线强度比值是可以用于反映样品的基体特征。 从以上结论中可以得出, 样品的基体元素和合金元素的谱线强度、 离子线与原子线的强度比值以及合金元素与基体元素的谱线强度比值均可对样品材料的表面硬度进行表征。

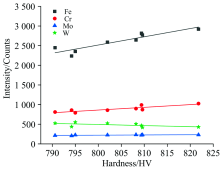图3 8个样品的基体元素、 合金元素的谱线强度与样品硬度的关系Fig.3 Relationships between the spectral line strengths of matrix elements and alloy elements and the hardness of 8 samples

图4 基体元素和合金元素的离子线与原子线的强度比值与样品硬度之间的关联性
(a): Fe Ⅱ 238.203 8 nm和Fe Ⅰ 404.581 3 nm的强度比值与样品硬度之间的关联性; (b): Cr Ⅱ 276.258 nm和Cr Ⅰ 425.433 1 nm的强度比值与样品硬度之间的关联性Fig.4 Correlations between the strength ratio of ion lines to atomic lines of matrix elements and alloying elements and sample hardness
(a): Correlation between the strength ratio of Fe Ⅱ 238.203 8 nm to Fe Ⅰ 404.581 3 nm and sample hardness; (b): Correlation between the strength ratio of Cr Ⅱ 276.258 nm to Cr Ⅰ 425.433 1 nm and sample hardness

图5 合金元素与基体元素的谱线强度比值与样品硬度之间的关联性
(a): Mo Ⅰ 313.259 4 nm和Fe Ⅰ 358.119 3 nm的强度比值与样品硬度之间的关联性; (b): W Ⅰ 283.138 nm和Fe Ⅰ 358.119 3 nm的强度比值与样品硬度之间的关联性Fig.5 Correlation between the spectral line strength ratio of alloying elements to matrix elements and sample hardness
(a): Correlation between the strength ratio of Mo Ⅰ 313.259 4 nm to Fe Ⅰ 358.119 3 nm and sample hardness; (b): Correlation between the strength ratio of W Ⅰ 283.138 nm to Fe Ⅰ 358.119 3 nm and sample hardness

2.2 建立硬度模型

2.2.1 利用谱线强度进行模型建立

为了对样品硬度进行定量分析, 采用SNV、 S-G卷积二阶导和高斯滤波三种不同的预处理方法对全波段谱线强度进行处理, 然后利用PLS算法建立定量模型。 模型采用KS算法将128个独立样本按2:1划分校正集和预测集, 即校正集为88个样本, 预测集为40个样本。 将模型LVs设为1~20, 直接取内部校正集预测误差值最小时对应的LVs, 建立车轮硬度预测模型。 模型评价指标如表3所示。 结果表明, LIBS技术与化学计量学分析方法相结合能够作为一种有效的钢材硬度检测方法, 其中采用SNV预处理后建立的PLS模型效果最佳。 如图6所示, 校正集的确定系数为0.98, 均方根误差为1.30, 预测集的确定系数为0.90, 均方根误差为2.43。

表3 所建模型的评价指标 Table 3 Evaluation index results of the model

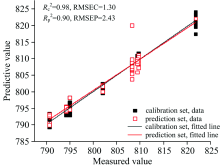图6 全波段谱线强度采用SNV预处理后建立模型的预测结果
2.2.2 结合谱线强度比值进行模型建立Fig.6 The prediction results of the model established using the full-band spectral line intensities after SNV pretreatment

在上述研究中, 通过利用全波段的谱线强度作为定量模型的输入获得了尚可接受的结果, 但是校正集和预测集的确定系数相差较大, 说明模型稳定性差, 且所建立的定量模型的均方根误差较大。 为寻求最优的硬度预测模型, 将谱线强度与谱线强度比值相结合作为变量进行定量模型的建立。 在此, 依据文献与NIST(美国国家标准与技术研究院)的标准原子光谱数据库, 人工挑出74条基体元素与合金元素的谱线, 它们之间互不干扰且分辨清晰, 如表4所示。

表4 人工挑出的基体元素与合金元素的谱线 Table 4 Spectral lines of manually selected matrix elements and alloy elements

表5所示为用于构成谱线强度比值的谱线, 当谱线在光谱仪的不同波长范围时, 将其用于构造谱线强度比值会受到光谱仪的响应特性差异影响, 因此需将谱线根据其波长所处光谱仪通道进行分组。 在此将其分为3组, 分别为200~240, 240~450和455~660 nm, 然后将被分在同一组的谱线两两进行配对, 将其对应谱线强度进行比值计算。

表5 用于计算谱线强度比值的谱线 Table 5 Spectral lines used to calculate spectral line intensity ratios

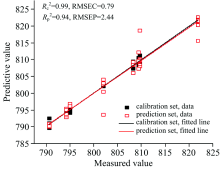
在变量谱线强度后直接拼接谱线强度比值, 再采用同上文所述的三种不同预处理方法对谱线强度与谱线强度比值相结合的变量进行处理, 然后利用PLS算法建立定量模型。 模型仍然采用KS算法按照2:1划分校正集和预测集。 将模型LVs设定为1~20, 模型指标结果如表6所示。 结果表明, 将谱线强度结合谱线强度比值原始数据作为变量所建立的PLS模型效果最佳。 如图7所示, 校正集的确定系数为0.99, 均方根误差为0.79, 预测集的确定系数为0.94, 均方根误差为2.44。

表6 模型的评价指标 Table 6 Evaluation index results of the model

图7 谱线强度结合谱线强度比值原始数据建立模型的预测结果Fig.7 Prediction results of the model established by combining the original data of spectral line intensity with the spectral line intensity ratio

通过两种变量采用相同预处理方法所建立模型的结果对比可以看出, 采用谱线强度结合谱线强度比值为变量的模型其预测集的确定系数均有所提高, 且校正集与预测集的确定系数的差值均有所减小, 说明模型预测的精确度及其稳定性都有所提升。 该结果说明, 将谱线强度和离子与原子线的强度比、 合金元素谱线强度与基体元素谱线强度的强度比相结合用作模型的输入变量, 能显著提升PLS模型对于金属材料表面硬度预测问题的解决, 并且构建了一种相关性更强的定量分析模型。 同时, 该结果也说明能够将谱线强度比看作是谱线的一种相对强度, 它可以降低由于激光烧蚀样品过程中能量不稳定所带来的光谱信号波动对实验造成的影响[15]。

3 结论

激光诱导击穿光谱技术(LIBS)不仅能对样品元素进行分析, 将其与化学计量学结合还可对金属材料的表面硬度进行预测和估算。 实验发现样品硬度与基体元素(Fe)和合金元素(Cr, Mo和W)的谱线强度、 离子与原子线的强度比值(Ⅱ /Ⅰ )以及合金元素谱线强度与基体元素谱线强度的强度比值(A/M)均可建立不同程度的相关关系, 并利用谱线强度、 谱线强度结合谱线强度比值作为变量分别建立了PLS定量模型, 以谱线强度为变量的模型中采用SNV预处理后建立的PLS模型效果最佳, 预测集的确定系数为0.90, 均方根误差为2.43。 以谱线强度结合谱线强度比值为变量的模型中采用原始数据建立的PLS模型效果最佳, 预测集的确定系数为0.94, 均方根误差为2.44, 且对比发现以谱线强度结合谱线强度比值为变量的模型其预测精确度及其稳定性相比于以谱线强度为变量的模型均有所提升。 研究表明, 采用激光诱导击穿光谱技术结合偏最小二乘法定量分析高铁车轮硬度具有一定可行性, 可将其用于现场诊断、 估算车轮表面硬度, 为维持高速列车安全运行提供一定的保障。

参考文献
[1] HUANG Ling(黄玲). China Basic Science(中国基础科学), 2018, 20(6): 61. [本文引用:1]
[2] Gan Feng, Dai Huanyun, Gao Hao, et al. Wear, 2015, 4(19): 569. [本文引用:1]
[3] Singh K, Khatirkar R K, Sapate S G. Wear, 2015, 328: 206. [本文引用:1]
[4] Dong M, Wei L, Lu J, et al. Journal of Analytical Atomic Spectrometry, 2019, 34(3): 480. [本文引用:1]
[5] Khajehzadeh N, Haavisto O, Koresaar L. Minerals Engineering, 2016, 98: 101. [本文引用:1]
[6] Meng D, Zhao N, Wang Y, et al. Spectrochimica Acta Part B: Atomic Spectroscopy, 2017, 137: 39. [本文引用:1]
[7] Sun L X, Yu H, Cong Z, et al. Spectrochimica Acta Part B: Atomic Spectroscopy, 2015, 112: 40. [本文引用:1]
[8] MA Cui-hong, ZHAO Yue-hua, MENG Fan-wei(马翠红, 赵月华, 孟凡伟). Laser Journal(激光杂志), 2018, 39(4): 30. [本文引用:1]
[9] Gómez-Nubla L, Aramendia J, de Vallejuelo S F O, et al. Microchemical Journal, 2018, 137: 392. [本文引用:1]
[10] Huang Jianwei, Dong Meirong, Lu Shengzi, et al. Journal of Analytical Atomic Spectrometry, 2018, 33(5): 673. [本文引用:1]
[11] JIA Hao-yue, GUO Gu-qing, ZHAO Fu-qiang, et al(贾皓月, 郭古青, 赵富强, 等). Spectroscopy and Spectral Analysis(光谱学与光谱分析), 2020, 40(12): 3895. [本文引用:1]
[12] Patel D N, Singh R P, Thareja R K. Applied Surface Science, 2014, 288: 550. [本文引用:1]
[13] Bilal M, Zou X B, Arslan M, et al. Journal of Near Infrared Spectroscopy, 2021, 29(4): 191. [本文引用:1]
[14] Huang J, Dong M, Lu S, et al. Journal of Analytical Atomic Spectrometry, 2018, 33(5): 720. [本文引用:1]
[15] Castro J P, Pereira-Filho E R. Journal of Analytical Atomic Spectrometry, 2016, 31(10): 2005. [本文引用:1]