作者简介: 李 元, 1984年生, 西安交通大学电力设备电气绝缘国家重点实验室副教授 e-mail: liyuan8490@xjtu.edu.cn
绝缘纸的老化状态决定了油浸式变压器的剩余寿命, 对绝缘纸的老化状态进行快速有效的评估具有重要意义。 聚合度是表征纤维素绝缘纸老化程度最直接可靠的参量, 在实验室中通过粘度法检测获得, 但该方法需要获得设备纸样, 不但检测耗时长, 还会对变压器类设备的绝缘造成破坏。 近红外光谱分析技术可以快速有效测定物质中的组分含量, 检测过程非侵入、 对绝缘无损, 目前已成功应用于多个领域, 有望成为替代传统聚合度检测的新方法。 然而, 现有的近红外光谱定量分析方法尚不能满足绝缘纸聚合度的预测精度需求, 建立了基于高斯过程回归(GPR)的绝缘纸老化状态定量评估方法。 构建了不同老化程度绝缘纸样本—近红外光谱数据库, 使用Savitzky-Golay卷积平滑算法对光谱数据进行平滑处理以提高信噪比; 研究了不同核函数GPR模型并开展了模型预测精度分析与参数敏感性检验。 结果显示, Exp核模型泛化性能较差, Matern32核、 Matern52核以及RQ核模型对参数敏感性较高、 模型稳定性较差, 最终选择了SE核GPR模型作为最优模型。 将SE核GPR模型与近红外分析领域常用的PLS, SVR与BPNN模型进行性能对比, 结果表明, GPR模型对校正集以及验证集样本的预测误差均最小(RMSE分别为65.5与70.6), 且预测结果与粘度法结果相关系数最高( r分别为0.94与0.93)。 与其他三种模型相比, GPR模型的RMSE比PLS, SVR与BPNN模型低54.1%, 58.8%和12.9%, 显示GPR模型在绝缘纸近红外光谱老化评估领域具有一定优势。
As the aging condition of the insulating papers determines the remaining lifetime of the oil-immersed transformers, a fast and effective aging assessment method for insulating paper is of great significance. As it is known, the degree of polymerization (DP) is the most direct parameter to characterize the aging condition of insulating papers. However, the traditional detection method or so-called viscometry is time-consuming and destructive. Near-infrared spectroscopy (NIRS) technology, as a non-destructive detection method can rapidly determine the samples' components and contents. Until now, it has been successfully applied in many fields and will hopefully be employed as an alternative method to viscometry. However, the current spectral quantitative analysis method is still not accurate enough to predict the DP of insulating paper samples. In this paper, we introduce Gaussian process regression (GPR) to predict DP of insulating papers accurately. Firstly, the NIRS database of insulating papers under different aging conditions is established, and in this procedure, the raw spectra are preprocessed by the Savitzky-Golay method to improve the signal ratio to noise. Then GPR models with various kernels are established, and the prediction accuracy and stability of the different models are comparatively studied. The results show that the GPR model with Exp kernel is of poor generalization performance, and the models with Matern32, Matern52 and RQ kernels are highly sensitive to the model parameters. Finally, the SE kernel is selected as the optimal kernel function of the GPR model. The DP prediction results of the SE kernel GPR model are compared with traditional PLS, SVR and BPNN models, and the results show that our established GPR model has the lowest RMSE (65.5 and 70.6) and highest correlation coefficient r (0.94 and 0.93), both for the training set and testing set. The RMSE of the GPR model is lower than PLS, SVR and BPNN models by 54.1%, 58.8% and 12.9% respectively. It is indicated that the established GPR model can be a powerful tool for the aging assessment of insulating papers by the NIRS technique.
大型油浸式电力变压器是输变电系统的关键设备, 其健康状态直接关系到电网的本质安全[1, 2]。 油纸复合绝缘是变压器的主要绝缘形式, 运行中长期承受电、 热、 机械、 环境等多重应力作用, 导致绝缘逐渐老化甚至失效[3, 4]。 绝缘油劣化后可方便地通过滤油、 祛气甚至换油实现状态更新, 而绝缘纸的老化进程却不可逆转, 而且老化后难以更换, 因此绝缘纸的老化状态基本上决定了变压器的剩余寿命。 聚合度是指纤维素分子链上葡萄糖单体的数量, 是表征绝缘纸老化状态最直接、 可靠的特征参量[5]。 传统的聚合度检测是将纸样研磨溶解后测量溶液粘度获得聚合度, 称为粘度检测法。 该方法准确度较高但检测耗时长, 还需要取得纸样, 对变压器的主绝缘具有破坏性。 在电网主设备智能运检的背景下, 提出一种检测快速、 无损便捷的绝缘纸聚合度评估方法具有重要意义。
近红外光谱分析技术可以对物质中的化学组分进行快速测定, 已在多个行业有效应用, 有望成为替代绝缘纸聚合度粘度法检测的新方法。 光谱定量分析方法是该技术的核心, 近年来已开展了不少研究。 李广茂等[6]利用偏最小二乘法(partial least squares regression, PLS)建立了绝缘油甲醇含量与拉曼光谱之间的定量分析模型, 实现变压器油中甲醇含量检测; 王书涛[7]利用支持向量回归机方法(support vector regression, SVR)解析柴油的近红外光谱数据, 准确预测了柴油密度、 粘度与凝点; 蒋有列等[8]通过将PLS、 反向传播神经网络(back propagation neural network, BPNN)方法应用于近红外光谱分析, 建立了绝缘油老化状态的定量分析模型, 结果表明BPNN模型的预测精度较高。
上述方法中, PLS是一种线性建模方法, 在油、 绝缘纸及水分共存时, 多种物质的光谱混叠, 增加了系统非线性, 导致PLS难以应对混合体系的定量分析。 SVR本质上是一种二分类方法, 在用于绝缘纸聚合度回归分析(多分类)时效果较差。 BPNN则容易陷入局部最优, 当数据库中样本数量较少时, 建立的神经网络模型很容易出现过拟合问题。
在对比PLS, SVR以及BPNN定量分析模型的基础上, 提出一种高斯过程回归(Gaussian process regression, GPR)的绝缘纸聚合度预测方法, 建立不同老化状态纸样的近红外光谱与其聚合度之间的准确关联。 通过模型精度分析与参数敏感性校验, 从不同核函数GPR模型中确定了最优模型; 进一步地, 将建立得到的GPR模型与通用的PLS, SVR与BPNN模型进行预测性能对比。 研究结果为绝缘纸老化状态的近红外光谱检测技术提供理论基础与模型参考。
通过加速热老化实验制备获得绝缘纸样本。 加速热老化实验平台由真空干燥箱、 干燥氮气以及老化皿等组成。 在分别对绝缘纸与绝缘油进行干燥、 除气处理后, 通过真空浸渍获得油纸绝缘样品。 在130 ℃条件下进行油纸绝缘样品的加速热老化实验, 定期取样获得478份不同老化程度的绝缘纸样本。
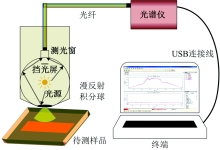
对制备得到的纸样采集漫反射近红外光谱, 如图1所示。 入射光在纸样和积分球表面发生多次漫反射, 反射光通过测光窗、 光纤传递至光谱仪进行分光, 与参比白板的标准光谱比对后得到纸样的近红外光谱。 光谱采集系统由Sol 2.2A便携式近红外光谱仪(美国B& W Tek公司)以及BWSpecTM光谱采集软件构成。 其中, 光谱仪检测单元为256单元铟镓砷阵列, 通过半导体制冷; 探头积分球与参比白板材质为聚四氟乙烯(PTFE)。 考虑到光谱仪自身暗噪声会影响光谱质量, 在光谱采集前需要记录暗电流水平, 设置光谱积分时间为600 μ s, 扫描次数为32次。
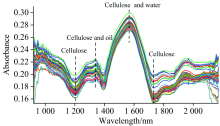
采集得到的典型绝缘纸样本的近红外光谱如图2所示, 可以发现样本光谱在1 220, 1 340, 1 540以及1 703 nm处具有明显的特征峰。 其中位于1 220 nm的C— H二级倍频、 1 703 nm的C— H一级倍频归属于纤维素[4], 当纤维素链受热断裂时, 上述特征峰会发生明显变化, 这是利用近红外光谱数据分析绝缘纸老化状态的理论基础。 但是, 位于1 340 nm处的C— H弱合频、 1 540 nm处的O-H一级倍频可同时归属于纤维素、 绝缘油与水分子, 组分信息混叠, 导致光谱特征峰与绝缘纸老化程度的关系并非肉眼可辨; 同时, 样品中混入的无关组分会影响预测结果, 因此需要借助光谱定量分析方法建立绝缘纸近红外光谱与老化程度之间的准确关联。
对制备得到的不同老化程度绝缘纸样进行聚合度检测, 检测方法为粘度滴定法[9]。 对每个样本进行两次聚合度检测, 取其平均值作为最终检测结果。 聚合度检测值作为标准值, 用于模型训练与性能评估。
1.4.1 高斯过程回归
本质上, GPR算法是在给定样本光谱数据分布的前提下得到对应样本聚合度值分布, 所得分布函数的数学期望即为GPR模型的聚合度预测结果。 GPR中假定绝缘纸聚合度y是由高斯分布函数f(x)以及噪声ε 组成[10], 同时有式(1)成立
式(1)中, 高斯分布函数f(x)由其期望m(x)以及方差k(x, x')决定, 即
式(2)中, k(x, x')的具体形式为核函数。
高斯过程同样假设噪声ε 符合高斯分布, 即
式(3)中,
由于任何有限的高斯序列可以组成一个独立的高斯过程[11], 因此y的分布同样符合高斯过程, 且该分布函数可通过f(x)以及ε 求解得到
式(4)中, δ (x, x')为克罗内克函数[12], 当且仅当x=x'时δ (x, x')=1, 否则δ (x, x')=0。
当输入待预测纸样的近红外光谱数据x* 时, 基于式(4)可以计算得到训练集绝缘纸样本聚合度与待测绝缘纸样本聚合度的联合分布, 如式(5)所示
式(5)中, K为方差矩阵, 通过式(6)求解
利用式(5)得到的联合分布可得边缘密度分布函数y* , 即待测绝缘纸样本聚合度的分布函数
求解得到的待测绝缘纸样本聚合度分布函数的数学期望即样本聚合度的预测结果。
1.4.2 模型建立过程
利用K-S(Kennard Stone)方法[13]将样本的光谱数据按8:2分为训练集与验证集, 其中训练集样本386个、 验证集92个。 在模型训练前利用SG(Savitzky-Golay)平滑方法[14]对光谱数据进行预处理, 降低光谱数据的噪声水平, 提高数据质量。
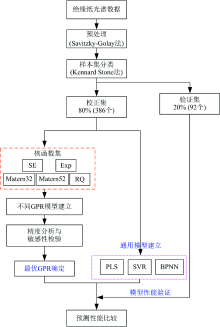
需要指出, 式(2)中核函数k(x, x')的类型对模型的预测能力有显著影响。 建立了基于不同核函数的GPR模型, 选用的核函数包括平方指数核(squared exponential, SE)、 指数核(exponential, Exp)、 有理二次核(rational quadratic, RQ)、 Matern32与Matern52核。 通过模型预测精度分析和参数敏感性检验, 确定最优核函数与GPR聚合度预测模型。 将得到的GPR模型与通用PLS, SVR以及BPNN模型进行聚合度预测性能横向比较。 GPR建模与性能比较流程如图3所示。
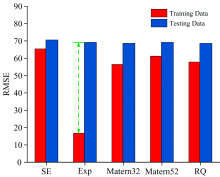
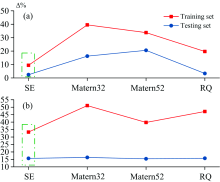
依据图3建立的基于不同核函数的GPR模型进行预测性能对比, 结果如图4所示, 图中纵轴表示样本均方根误差(root mean square error, RMSE)。 其中Exp核模型对训练集数据的RMSE远高于验证集, 出现严重的过拟合现象, 因此先将该核函数剔除。 而其余核函数GPR模型的预测准确度差异尚不显著, 需要通过参数敏感性检验进一步筛选最优核函数。
通过多次试验发现, 提高式(4)中噪声分布函数方差的下限σ n_low会显著降低模型预测准确度。 参数敏感性校验是通过改变σ n_low来检查模型RMSE的相对变化率Δ , 计算方法如式(8)所示。 Δ 越小表示模型对该参数的敏感性越低, 即在不同参数条件下模型的性能可以保持稳定。 图4所示结果是在σ n_low=60的情况下得到的, 现给定参数扰动δ 。 根据Δ 表现判定各核函数GPR模型的稳定性, 检验结果如图5所示。 由图可知, δ =30或60时, 四种核函数模型的RMSE均有不同程度的增加, 其中SE内核模型的Δ 最小, SE内核回归模型相较于其他模型具有更高稳定性, 因此将SE核函数作为GPR模型的最优核函数。
式(8)中, δ 为参数扰动。
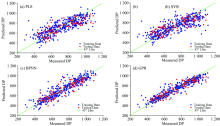
将建立的最优GPR模型与通用PLS, SVR和BPNN三种聚合度预测模型的性能比较如图6所示。 较为明显地, BPNN模型[图6(c)]与GPR模型[图6(d)]的预测效果较好, 而PLS模型[图6(a)]与SVR模型[图6(b)]预测效果则稍差。
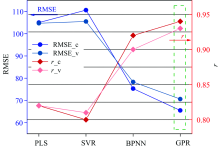
利用RMSE与相关系数r定量表征四种模型的预测效果, 结果如表1所示。 其中SVR模型性能最差, 该模型对校正集样本以及验证集样本的预测RMSE分别为110.6与105.5。 GPR模型的效果最优, 对校正集以及验证集样本的预测结果均具有最小的RMSE(65.5与70.6)。 四种模型的RMSE与r曲线如图7所示, 其中RMSEc与RMSEv分别表示校正集与验证集的均方根误差, rc与rv表示校正集与验证集的相关系数, 图中表明四种模型对绝缘纸聚合度的预测准确度排序为: GPR> BPNN> PLS> SVR。
| 表1 不同绝缘纸聚合度预测模型性能比较 Table 1 Comparison of different DP prediction models for insulating paper |
通过加速热老化实验制备获得不同老化程度的绝缘纸样品, 建立了绝缘纸的近红外光谱数据库, 提出了绝缘纸聚合度的GPR预测模型。 主要研究结论如下:
(1)考虑到核函数的类型对GPR模型的预测准确度影响较大, 建立了基于多种核函数的GPR模型, 对模型进行参数敏感性检验, 研究结果发现SE核GPR模型不但能克服过拟合问题, 而且模型的参数敏感性低, 稳定性最好, 由此筛选出基于SE核的最优GPR聚合度预测模型。
(2)与近红外光谱领域常用预测模型横向比较显示, 研究提出的GPR聚合度预测模型准确度最高, 其预测误差分别低于PLS, SVR与BPNN模型误差54.1%, 58.8%和12.9%。 研究结果证实了利用GPR方法准确预测绝缘纸聚合度的可行性。
(3)基于高斯过程回归的绝缘纸聚合度近红外光谱评估模型检测精度较高, 相比于传统检测方法(粘度法)检测方便快捷, 具有更加广泛的应用场景, 能够更好的服务于变压器绝缘老化诊断与运行评价。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|