引用本文
郑玉霞, 帕尔哈提江#cod#x000b7;吐尔孙, 热米莱#cod#x000b7;阿卜来提, 程龙, 马登攀. 多分散Au-Ag合金纳米球的光谱消光法反演[J]. 光谱学与光谱分析, 2022,42(10): 3039-3045.
ZHENG Yu-xia, TUERSUN Paerhatijiang, ABULAITI Remilai, CHENG Long, MA Deng-pan. Retrieval of Polydisperse Au-Ag Alloy Nanospheres by Spectral Extinction Method[J]. Spectroscopy and Spectral Analysis, 2022,42(10): 3039-3045.
Doi:10.3964/j.issn.1000-0593(2022)10-3039-07  
Permissions
Copyright©2022, 《光谱学与光谱分析》期刊社
《光谱学与光谱分析》期刊社 所有
多分散Au-Ag合金纳米球的光谱消光法反演
郑玉霞1,2, 帕尔哈提江·吐尔孙1,2,*, 热米莱·阿卜来提1,2, 程龙1,2, 马登攀1,2
1.新疆师范大学物理与电子工程学院, 新疆 乌鲁木齐 830054
2.新疆发光矿物与光功能材料研究重点实验室, 新疆 乌鲁木齐 830054
*通讯作者 e-mail: ptuersun@163.com

作者简介: 郑玉霞, 1995年生, 新疆师范大学物理与电子工程学院硕士研究生 e-mail: dearprof@126.com

收稿日期: 2021-09-15 修回日期: 2021-12-14 接受日期: 2021-12-14
基金: 新疆维吾尔自治区自然科学基金项目(2021D01A116), 国家自然科学基金项目(11764042), 新疆矿物发光材料及其微结构重点实验室招标课题(KWFG2003)资助
摘要

贵金属纳米颗粒具有局域表面等离子体共振特性而引起了广泛的关注, 其中Au-Ag合金纳米颗粒具有良好的结构稳定性、 光热性能以及潜在的抗癌功效而得到普遍研究。 在众多应用中的特性与其粒径和浓度密切相关, 然而目前常用的电子显微镜观察法和动态光散射法不能同时获得粒径和浓度信息, 因此采取有效手段测量颗粒粒径和浓度信息至关重要。 基于光谱消光法, 利用非负的Tikhonov正则化方法解决反演问题, 并根据Mie理论计算消光矩阵。 针对噪声问题, 采取两种情况研究多分散Au-Ag合金纳米球粒径分布与浓度的反演问题。 未添加噪声情况下, 颗粒系Ⅰ的反演相对误差小于颗粒系Ⅱ, 在波长范围300~500 nm之间的反演相对误差最小, 对应平均粒径、 粒径标准差和颗粒数浓度的反演相对误差分别为0%,-0.03%和0%。 添加随机噪声情况下, 将0.5%和1.0%的随机噪声添加进颗粒系Ⅰ中的消光谱, 经过数据比较发现在波长范围200~600 nm之间的反演相对误差最小。 当添加0.5%的随机噪声时, 粒径分布、 粒径标准差和颗粒数浓度的变化范围分别为79.76~80.15 nm, 5.60~6.61 nm和0.995 8×1010~1.005 9×1010个·cm-3; 当添加1.0%的随机噪声时, 粒径分布、 粒径标准差和颗粒数浓度的变化范围分别为78.87~80.27 nm, 5.36~9.00 nm和0.992 4×1010~1.027 7×1010个·cm-3。 反演结果随着随机噪声的增大, 变化范围也明显增大即反演相对误差增大, 并且每次添加相同随机噪声后的反演结果不同。 为了减少随机噪声导致的不稳定性, 对100次反演结果进行平均得到平均粒径、 粒径标准差和颗粒数浓度。 当随机噪声从0.5%增大至1.0%时, 其反演结果的相对误差均增大, 但是反演得到的粒径分布、 粒径标准差和颗粒数浓度相对误差均小于6%, 这说明通过反演算法得到的反演结果具有较好的稳定性。 研究表明, 光谱消光法为反演多分散Au-Ag合金纳米球粒径分布与浓度提供了一种简单、 快速的表征手段, 也对研究非球形纳米颗粒有启示作用。

关键词: 消光法; 光谱分析; 复合纳米材料; 局域表面等离子体共振; Mie理论; Tikhonov正则化
中图分类号:O433.4 文献标志码:A
Retrieval of Polydisperse Au-Ag Alloy Nanospheres by Spectral Extinction Method
ZHENG Yu-xia1,2, TUERSUN Paerhatijiang1,2,*, ABULAITI Remilai1,2, CHENG Long1,2, MA Deng-pan1,2
1. School of Physics and Electronic Engineering, Xinjiang Normal University, Urumqi 830054, China
2. Key Laboratory for Luminescence Minerals and Optical Functional Materials of Xinjiang, Urumqi 830054, China
*Corresponding author
Abstract

Noble metal nanoparticles have attracted much attention because of their local surface plasmon resonance properties, among which Au-Ag alloy nanoparticles have widespread investigated for their good structural stability, photothermal properties, and potential anticancer efficacy. The properties in many applications are closely related to particle size and concentration. However, the currently used electron microscopy observation method, and dynamic light scattering method cannot obtain both particle size and concentration information, so it is very important to take effective means to measure particle size and concentration. Based on the spectral extinction method, the inversion problem is solved using a non-negative Tikhonov regularization method and the extinction matrix is calculated using the Mie theory. For the noise problem, two cases are adopted to study the inversion of the particle size distribution and concentration of polydisperse Au-Ag alloy nanospheres. In the case of without noise, the inversion error of particle systems Ⅰ is smaller than that of particle systems Ⅱ, and the inversion error is the smallest in the wavelength range of 300~500 nm, where the inversion errors of the mean particle size, the standard deviation of particle size, and the particle number concentration are 0%, -0.03%, and 0%, respectively. In the case of adding random noise, 0.5% and 1.0% random noises were added to the extinction spectrum of particle systems Ⅰ. The inversion error was the smallest in the wavelength range of 200~600 nm. When 0.5% random noise was added, the ranges of particle size distribution, the standard deviation of particle size, and particle number concentration were 79.76~80.15 nm, 5.60~6.61 nm, and 0.995 8×1010~1.005 9×1010 particle·cm-3, respectively; when 1.0% random noise was added, the ranges of particle size distribution, the standard deviation of particle size, and particle number concentration were 78.87~80.27 nm, 5.36~9.00 nm, and 0.992 4×1010~1.027 7×1010 particle·cm-3, respectively. It was found that with the increase of random noise, the variation range of the inversion result also increased significantly (i. e., the relative error of the inversion increases). The mean particle size, the standard deviation of particle size, and the particle number concentration were averaged after 100 random noise sequences were added. When the random noise increases from 0.5% to 1.0%, the relative errors of the inversion results increase, but the relative errors of the particle size distribution, the standard deviation of particle size, and the particle number concentration are less than 6%. It indicates that the inversion results obtained by the algorithm have good stability. This investigation shows that the spectral extinction method provides a simple and rapid characterization means for the inversion of particle size distribution and concentration of polydisperse Au-Ag alloy nanospheres, and also has enlightenment for the investigation of non-spherical nanoparticles.

Keyword: Light extinction; Spectroscopic analysis; Nanocomposites; Localized surface plasmon resonance; Mie theory; Tikhonov regularization
引言

通常纳米颗粒的粒径范围在1~100 nm之间, 当颗粒粒径达到纳米级别时, 将会产生许多独特的性质, 于是纳米材料的研究与制备得到迅速发展[1]。 尤其是金属纳米颗粒, 在入射光激发下会产生局域表面等离子体共振(localized surface plasmons resonance, LSPR)现象[2], 表现出与体相材料所不同的优异特性。 其中复合纳米材料得到广泛研究, 不仅可以显示其组成成分的性质, 而且还可以显示出由组合的协同作用所产生的新特性[3]。 因此, 在生物传感与检测[4]、 表面增强拉曼散射[5]、 医学成像[6]等方面金属纳米颗粒都有着广泛的应用。

在不同纳米结构的复合纳米材料中, Au具有化学惰性且表现出稳定的等离子体响应, 但其高成本已成为主要缺点。 Ag的成本较低且等离子体活性强于Au, 但较差的稳定性限制了其实用性。 将这两种金属进行合成并制备出不同形状和大小的Au-Ag合金纳米颗粒已成为一种新兴纳米材料。 研究发现, Ag纳米颗粒对众多细菌菌株表现出有效抗菌性, 合成的Au-Ag合金纳米颗粒可以通过调整Ag的摩尔分数, 从而更好地保持有效的抗菌活性以限制哺乳动物体内的病毒活性[7]。 在有机发光器件方面, Au-Ag合金纳米颗粒可以同时增加辐射强度和抑制非辐射损失, 这有利于提高发射器的量子产率和发光效率[8]。 于是, 合金纳米颗粒比较于单金属纳米颗粒而言, 在各方面显示出更加优异的性能, 并且具有众多潜在应用。

Au-Ag合金纳米颗粒的光学特性与LSPR的影响因素具有十分紧密的联系, 其强烈依赖于粒径和浓度。 因此, 对Au-Ag合金纳米颗粒的粒径和浓度进行有效调控是至关重要的, 其将决定合金纳米颗粒的性能和应用[9, 10]。 在众多粒径测量方法中光谱消光法因其原理简单、 方便, 并且可以同时获得粒径和浓度信息而备受关注[11]。 目前, 利用光谱消光法反演多分散Au-Ag合金纳米球颗粒系的研究还鲜有报道。 因此, 从理论上研究多分散Au-Ag合金纳米球颗粒系的光谱消光法, 定量分析了波长范围、 平均粒径、 粒径分布宽度及随机噪声对反演结果的影响, 这为后续的实验研究提供理论指导。

1 理论方法

在单次散射条件下, 穿过颗粒系的透射光强It由比尔-朗伯(Beer-Lambert)定律[12]表示为

It=Iiexp(-αextL)(1)

式(1)中, Ii为入射光强度, α ext为衰减系数, L为光程。 当两个颗粒的间隔超过颗粒自身粒径D的2.5倍时, 位移可以忽略不计即光散射满足不相干的单次散射[13]。 于是, 计算颗粒间隔为3倍时最大的颗粒数浓度约为1021/(4D)3个· cm-3, 当粒径为100 nm时对应最大的颗粒数浓度约为1.562 5× 1013个· cm-3。 因此, 利用光谱消光法反演颗粒粒径和浓度时, 要求被测颗粒数浓度需小于或等于最大颗粒数浓度。

在光谱消光法中, 吸光度A表示衰减程度, 即分光光度计在紫外到可见光范围内颗粒的测量参数[14], 则单分散颗粒系的吸光度A1可以由式(1)得到

A1(λ)=log10(Ii/It)=LNln(10)Cext(λ, D, np, nm)(2)

式(2)中, N为颗粒数浓度, Cext为单个颗粒的消光截面, Cext为入射光波长λ 、 被测颗粒粒径D、 颗粒折射率np和周围环境折射率nm的函数。 其中Au-Ag合金纳米球的周围环境折射率nm, 即在室温(20 ℃)下水的折射率[15], 消光截面由Mie理论[16]数值计算求出。

在实际生产应用中往往不存在理想的单分散颗粒系, 而是将多分散颗粒系近似等效为单分散颗粒系。 于是, 多分散颗粒系的吸光度A2可表示为

A2(λ)=log10(Ii/It)=LNln(10)·∑j=1Jp(Dj)Cext(λ, Dj, np(λ, Dj), nm(λ))(3)

式(3)中, p(Dj)表示粒径分布函数, 其必须满足标准归一化条件, 即

∑j=1Jp(Dj)=1(4)

式(3)中, 多分散颗粒系的吸光度A2可反演的粒径分布和浓度满足线性方程关系, 可写为

A=CP(5)

式(5)中, C, P和A的表达式分别为

C=Lln(10)Cext(λ1, D1)Cext(λ1, D2)...Cext(λ1, DJ)Cext(λ2, D1)Cext(λ2, D2)...Cext(λ2, DJ)︙︙⋱︙Cext(λI, D1)Cext(λI, D2)...Cext(λI, DJ)(6)

P=N[p(D1)p(D2)...p(Dj)...p(DJ)]T(7)

A=[A(λ1)A(λ2)...A(λi)...A(λI)]T(8)

其中i和j是整数, 上标T表示向量的转置。 C为I× J矩阵, 即每对波长和粒径计算得出的消光截面; P为J× 1矢量, 为要求解的未知数; A为I× 1矢量, 即不同波长下通过实验测量得到的吸光度(消光谱)。 在数学上, 检索多分散Au-Ag合金纳米球颗粒系的粒径分布和浓度是一个反演问题。 利用非负Tikhonov正则化方法求解该线性方程, 并研究反演问题得到其唯一解[17], 其中粒径和波长的离散值被用于反演。

计算消光截面时纳米颗粒的折射率可以由介电函数计算得到, 即np=ε 1/2。 利用Rioux等[18]建立且可预测的Drude-Lorentz模型, 在Au-Ag合金中当Au的摩尔分数改变时, 消光谱的共振波长也会相应发生改变。 于是, 选择合金中Au的摩尔分数为50%时, 即Au与Ag纳米颗粒完全混合情况下等摩尔分数比例的Au-Ag合金纳米球作为研究对象。 通过Mie理论预测并反演得到合金纳米颗粒的消光谱, 得到的反演光谱与实验光谱具有优异的一致性。

2 结果与讨论

单分散颗粒系在可见消光谱范围内的粒径强烈依赖于共振波长, 且具有一一对应的关系[14]。 即由分光光度计测量并确定吸光度最大值所对应的共振波长, 就可以获得其粒径D和颗粒数浓度N的信息。

对于多分散颗粒系, 光谱消光法同样适用于反演Au-Ag合金纳米球的粒径分布和浓度。 因此, 首先需要确定多分散颗粒系的参数, 颗粒系Ⅰ 的平均粒径Dm和粒径标准差σ 分别选取为80和6 nm; 颗粒系Ⅱ 的平均粒径Dm和粒径标准差σ 分别选取为30和5 nm, 颗粒数浓度均取为1× 1010个· cm-3。 反演所用到的参数则选择200~600 nm之间的波长范围, 波长离散数目为101个点, 颗粒系的粒径范围从Dm-4σ 增加到Dm+4σ , 粒径离散数目为31个点, 光程为1 cm。 然而, 在实际测量中噪声是不可忽略的影响因素, 于是分两种情况对多分散Au-Ag合金纳米球颗粒系进行定量分析并讨论其反演结果。

2.1 未添加噪声情况下的数值反演

假设为理想情况, 即反演过程消光谱中未添加噪声干扰的情况下, 研究波长范围对反演结果的影响。 分别对颗粒系Ⅰ 与颗粒系Ⅱ 的参数进行数值反演, 在200~600 nm波长范围内选取10组波段, 即200~300, 200~400, 200~500, 200~600, 300~400, 300~500, 300~600, 400~500, 400~600以及500~600 nm。 在不同波段范围内, 分别得到颗粒系Ⅰ 与颗粒系Ⅱ 的10组参数所对应的反演结果, 即平均粒径Dm、 粒径标准差σ 和颗粒数浓度N的反演相对误差, 如表1所示。 从表中数据可以明显得出结论, 对于颗粒系Ⅰ 与颗粒系Ⅱ , 波长范围在300~500 nm之间反演结果的相对误差均为最小。 在颗粒系Ⅰ 中, Dm, σ 和N的反演相对误差分别为0%, -0.03%和0%。 在颗粒系Ⅱ 中, Dm, σ 和N的反演相对误差分别为+0.06%, -1.19%和-0.04%。 因此, 通过光谱消光法反演颗粒系粒径分布与浓度时, 应选择平均粒径Dm、 粒径标准差σ 和颗粒数浓度N的反演相对误差较小的波长范围, 以获得最好的反演结果。

表1 不同波长范围对应的颗粒系Ⅰ 与颗粒系Ⅱ 反演误差 Table 1 Inversion errors of particle ensembles Ⅰ and particle ensembles Ⅱ in different wavelength ranges

于是, 利用光谱消光法数值反演两种多分散颗粒系, 得到粒径分布的反演结果与原始结果, 如图1(a)和图2(a)所示; 消光谱的重建结果与原始结果, 如图1(b)和图2(b)所示。 颗粒系Ⅰ 反演获得的粒径分布结果明显优于颗粒系Ⅱ , 颗粒系Ⅰ 的反演结果与原始粒径分布完全重合, 颗粒系Ⅱ 的反演结果与原始粒径分布基本一致; 颗粒系Ⅰ 与颗粒系Ⅱ 反演获得的重建结果与原始消光谱均完全重合。 得出结论在未添加噪声情况下, 在300~500 nm波长范围内, 颗粒系Ⅰ 反演的相对误差均小于颗粒系Ⅱ , 并且反演的粒径分布与消光谱拟合结果较好。 然而, 由图1和图2可以明显看出, 颗粒系Ⅰ 与颗粒系Ⅱ 反演的消光谱始终与原始结果保持高度吻合, 反演的粒径分布却存在明显偏差, 即粒径分布的反演结果受平均粒径和粒径标准差影响。 于是, 进一步反演得到平均粒径Dm、 粒径标准差σ 和颗粒数浓度N的相对误差, 其随着平均粒径和粒径标准差的变化范围进行讨论。

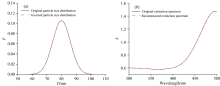图1 颗粒系Ⅰ 反演结果与原始分布的比较
(a): 粒径分布; (b): 消光谱Fig.1 Comparison of inverted results with original distribution for particle systems Ⅰ
(a): Particle size distribution; (a): Extinction spectrum

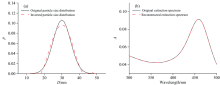图2 颗粒系Ⅱ 反演结果与原始分布的比较
(a): 粒径纷布; (b): 消光谱Fig.2 Comparison of inverted results with original distribution for particle systems Ⅱ
(a): Particle size distribution; (a): Extinction spectrum

在上一部分颗粒系Ⅰ 与颗粒系Ⅱ 确定的参数中, 平均粒径Dm、 粒径标准差σ 和颗粒数浓度N均取为定值, 然而, 反演结果与平均粒径和粒径标准差的取值影响较大。 于是, 分别定量讨论平均粒径和粒径标准差所产生的反演相对误差。 首先, 将粒径标准差固定为6 nm, 平均粒径的范围为30~90 nm, 步长为10 nm, 如图3(a)所示。 随着平均粒径的增大, 平均粒径的反演相对误差从-2.72%减小到0%, 粒径标准差的反演相对误差从21.98%减小到-0.03%, 颗粒数浓度的反演相对误差从5.12%减小到0%。 然后, 将平均粒径固定为60 nm, 粒径标准差的范围为3~9 nm, 步长为1 nm, 如图3(b)所示。 随着粒径标准差的增大, 平均粒径的反演相对误差从-1.07%减小到0.11%, 粒径标准差的反演相对误差从47.78%减小到1.00%, 颗粒数浓度的反演相对误差从2.27%减小到-0.19%。 定量分析得出结论, 当平均粒径Dm与粒径标准差σ 的取值范围逐渐增大时, 平均粒径Dm、 粒径标准差σ 和颗粒数浓度N的反演相对误差均减小, 且趋近于0%, 所得反演结果更为准确。

图3 反演相对误差随平均粒径和粒径标准差的变化
(a): 反演相对误差随平均粒径的变化; (b): 反演相对误差随粒径标准差的变化Fig.3 Variations of inversion relative error with mean particle size and particle size distribution standard deviation
(a): Variation of inversion relative error with mean particle size; (b): Variation of inversion relative error with particle size distribution standard deviation

2.2 添加随机噪声情况下的数值反演

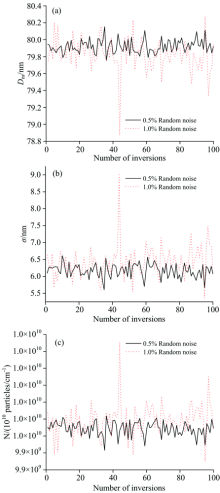
噪声是不确定因素, 但是通过数值反演可以估算出随机噪声对反演结果的影响。 已知在未添加噪声情况下颗粒系Ⅰ 的反演相对误差最小, 因此将0.5%和1.0%的随机噪声添加进颗粒系Ⅰ 中的消光谱。 经过大量数据对比分析发现, 在波长范围200~600 nm之间添加随机噪声时, 反演结果的相对误差最小。 为了研究在颗粒系Ⅰ 中添加0.5%和1.0%随机噪声产生的反演相对误差, 于是分别给出添加随机噪声后, 反演的粒径分布与重建的消光谱, 如图4和图5所示。 反演的粒径分布与原始的粒径分布存在明显偏差, 反演的消光谱与原始的消光谱基本完全一致。 然而, 在添加相同随机噪声的情况下, 会产生不同的反演结果, 即反演过程不稳定。 因此, 对所添加的随机噪声计算了100次反演结果, 反演得到粒径分布、 粒径标准差和颗粒数浓度随噪声序列的变化情况, 如图6所示。 当随机噪声从0.5%增大至1.0%时, 反演结果随着随机噪声的增大, 变化范围明显增大。 当随机噪声为0.5%时, 粒径分布范围为79.76~80.15nm, 粒径标准差范围为5.60~6.61 nm, 颗粒数浓度范围为0.995 8× 1010~1.005 9× 1010个· cm-3; 当随机噪声为1.0%时, 粒径分布范围为78.87~80.27 nm, 粒径标准差范围为5.36~9.00 nm, 颗粒数浓度范围为0.992 4× 1010~1.027 7× 1010个· cm-3。

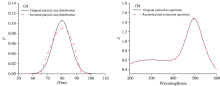图4 添加0.5%随机噪声后的反演结果
(a): 粒径分布; (b): 消光谱Fig.4 Inversion results after adding 0.5% random noise
(a): Particle size distribution; (b): Extinction spectrum

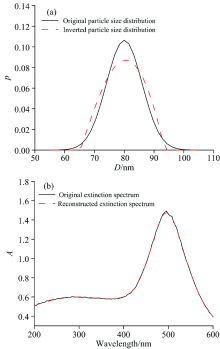图5 添加1.0%随机噪声后的反演结果
(a): 粒径分布; (b): 消光谱Fig.5 Inversion results after adding 1.0% random noise
(a): Particle size distribution; (b): Extinction spectrum

图6 添加0.5%和1.0%随机噪声后的反演结果 (计算100次反演结果)
(a): 平均粒径; (b): 粒径标准差; (c): 颗粒数浓度Fig.6 Comparison of the inversion results with the original distribution after adding 0.5% random noises (Calculated 100 inversion results)
(a): Mean particle size; (b): Standard deviation of particle size; (c): Particle number concentration

为了更好的反演获得粒径分布、 粒径标准差和颗粒数浓度的相对误差, 于是对添加随机噪声计算得到的100次反演结果进行平均, 并获得反演结果与原始结果的参数比较, 如表2所示。 当随机噪声从0.5%增大至1.0%时, 平均粒径的反演相对误差从-0.09%增大至-0.19%, 粒径标准差的反演相对误差从+2.31%增大至+5.72%, 颗粒数浓度的反演相对误差从+0.18%增大到+0.43%。 得到的反演结果表明, 平均粒径和颗粒数浓度的反演相对误差均较小, 粒径标准差的反演相对误差较大, 但得到的反演相对误差均小于6%, 这说明反演算法得到的反演结果具有较好的准确性与稳定性。

表2 原始和反演参数的比较(对100次反演结果进行平均得到) Table 2 Comparison of original and inversion parameters (obtained by averaging 100 inversion results)
3 结论

基于光谱消光法, 研究多分散Au-Ag合金纳米球颗粒系粒径分布与浓度的反演问题。 在未添加噪声情况下, 在300~500 nm波长范围之内, 反演平均粒径、 粒径标准差和颗粒数浓度的相对误差均为最小。 在消光谱中添加随机噪声情况下, 当随机噪声从0.5%增大至1.0%时, 反演结果的相对误差也将增大, 且均小于6%, 这说明反演算法具有较好的稳定性和可靠性。 研究表明, 光谱消光法可以用于测量多分散Au-Ag合金纳米球颗粒系的粒径分布与浓度。 光谱消光法具有重要的应用价值和研究意义, 为显微成像分析提供了一种有吸引力的替代方法。 纳米颗粒测量得到的消光谱信息不仅适用于反演非球形纳米颗粒的粒径分布和浓度, 而且还适用于反演未知的Au-Ag合金纳米颗粒摩尔分数比例。

参考文献
[1] Slepicka P, Kasálková N S, Siegel J, et al. Materials, 2020, 13(1): 1. [本文引用:1]
[2] Mulvaney P. Langmuir, 1996, 12(3): 788. [本文引用:1]
[3] Marin I M, Asensio J M, Chaudret B. ACS Nano, 2021, 15(3): 3550. [本文引用:1]
[4] Biasotto G, Costa J P C, Costa P I, et al. Applied Physics A, 2019, 125(12): 821. [本文引用:1]
[5] DOU Xin-yi, ZHANG Can, ZHANG Jie(窦心怡, 张灿, 张洁). Spectroscopy and Spectral Analysis(光谱学与光谱分析), 2021, 41(5): 6. [本文引用:1]
[6] Jin K T, Yao J Y, Ying X J, et al. Current Topics in Medicinal Chemistry, 2020, 30(2): 2737. [本文引用:1]
[7] Lin Z, Luo Y, Liu P F, et al. Colloids and Surfaces B: Biointerfaces, 2021, 204: 111831. [本文引用:1]
[8] Liu B, Januar M, Cheng J C, et al. Nanoscale, 2021, 13(28): 12164. [本文引用:1]
[9] Xu C J, Tung G A, Sun S H. Chemistry of Materials, 2008, 20(13): 4167. [本文引用:1]
[10] Chand er N, Khan A F, Thouti E, et al. Solar Energy, 2014, 109: 11. [本文引用:1]
[11] Hinterwirth H, Wiedmer S K, Moilanen M, et al. Journal of Separation Science, 2013, 36(17): 2952. [本文引用:1]
[12] Lindquist N C, Nagpal P, McPeak K M, et al. Reports on Progress in Physics, 2012, 75(3): 036501. [本文引用:1]
[13] Su K H, Wei Q H, Zhang X, et al. Nano Letters, 2003, 3(8): 1087. [本文引用:1]
[14] Tuersun P, Zhu C J, Han X E, et al. Optik, 2020, 204: 163676. [本文引用:2]
[15] Daimon M, Masumura A. Applied Optics, 2007, 46(18): 3811. [本文引用:1]
[16] Mie G. Annals of Physics, 1908, 25: 377. [本文引用:1]
[17] Mroczka J, Szczuczyński D. Applied Optics, 2012, 51(11): 1715. [本文引用:1]
[18] Rioux D, Vallières S, Besner S, et al. Advanced Optical Materials, 2014, 2(2): 176. [本文引用:1]