引用本文
朱玲, 秦凯, 李明, 赵英俊. 改进的堆栈稀疏自编码矿物高光谱端元识别研究[J]. 光谱学与光谱分析, 2021,41(4): 1288-1293.
ZHU Ling, QIN Kai, LI Ming, ZHAO Ying-jun. Research on Improved Stacked Sparse Autoencoders for Mineral Hyperspectral Endmember Extraction[J]. Spectroscopy and Spectral Analysis, 2021,41(4): 1288-1293.
Doi:10.3964/j.issn.1000-0593(2021)04-1288-06  
Permissions
Copyright©2021, 《光谱学与光谱分析》期刊社
《光谱学与光谱分析》期刊社 所有
改进的堆栈稀疏自编码矿物高光谱端元识别研究
朱玲, 秦凯*, 李明, 赵英俊
核工业北京地质研究院遥感信息与图像分析技术国家级重点实验室, 北京 100029
*通讯作者 e-mail: h_rs_qk@163.com

作者简介: 朱 玲, 1992年生, 核工业北京地质研究院遥感信息与图像分析技术国家级重点实验室助理工程师 e-mail: thal_zhu@163.com

收稿日期: 2020-03-02 修订日期: 2020-07-21
基金: 国家自然科学基金青年科学基金项目(41602333)资助
摘要

自然界中岩石一般是由多种矿物集合而成的紧致混合物, 由于高光谱传感器低空间分辨率的特征, 获得的高光谱数据多为矿物组分的综合反映。 受噪声干扰以及矿物复杂的混合机理等因素影响, 高光谱端元识别和定量分析成为目前研究的热点与难点。 基于深度学习理论, 对原始自编码结构进行改进, 提出了一种改进的堆栈稀疏自编码的矿物高光谱端元识别方法(stacked sparse autoencoders, SSAE), 为高光谱解混提供新的思路。 首先, 根据矿物混合光谱的特点, 对原始自编码结构进行三点改进: 第一, 去掉自编码神经网络的偏置项(bias); 第二, 在隐藏层激活函数之前添加批归一化(batch normalization, BN)层, 最后一层输出层使用Relu激活函数; 第三, 用光谱角函数( LSAD)代替均方误差( LMSE)作为目标函数。 SSAE法通过梯度下降方式对目标函数进行优化求解获取神经网络参数。 然后, 利用Hapke模型建立不同矿物组合和不同质量分数的两个模拟数据集, 数据集共包括高岭石、 叶腊石、 蒙脱石、 绿泥石、 白云母、 方解石、 赤铁矿、 白云石、 钾长石和褐铁矿10种常见矿物光谱。 最后, 利用SSAE方法对模拟数据集进行端元提取测试, 测试结果与网络结构改进过程中产生的6种情况以及顶点成分分析法(VCA)和基于最小体积的变元切分增量拉格朗日单形体识别算法(SISAL)提取结果进行比较。 实验证明, 本研究提供的是一种盲端元识别方法, 改进后的SSAE神经网络端元提取精度比未完成改进前有明显提升。 SSAE法可以成功识别两个模拟数据集所有的端元, 光谱角距离(spectral angle distance, SAD)的平均误差分别为0.0597和0.0344, 与VCA法提取精度差异较小, 均优于SISAL法的识别结果。 SSAE法为矿物高光谱解混提供了新的方向, 对高光谱遥感的地质应用和高光谱遥感定量分析研究具有较好的促进作用。

关键词: 堆栈稀疏自编码; 神经网络; 端元识别; 高光谱; 矿物
中图分类号:P258 文献标志码:A
Research on Improved Stacked Sparse Autoencoders for Mineral Hyperspectral Endmember Extraction
ZHU Ling, QIN Kai*, LI Ming, ZHAO Ying-jun
National Key Laboratory of Remote Sensing Information and Imagery Analyzing Technology, Beijing Research Institute of Uranium Geology, Beijing 100029, China
*Corresponding author
Abstract

Rocks in nature are usually aggregates of various minerals. Due to the low spatial resolution of hyperspectral sensors, the hyperspectral data obtained are mostly the mixing spectrum of mineral components. Affected by factors such as noise interference and intimate mixing characteristics of minerals, endmember extracting and quantifying analysis of minerals is still a hotspot and difficulty topicin current research. Based on the deep learning theory, this study improves the autoencoder structure and proposes a new stacked sparse autoencoders method (SSAE), which provides a new idea for mineral hyperspectral unmixing. First of all, according to the characteristics of mineral mixing spectrum, three improvements have been made: first, the bias term of autoencoder neural network is removed; second, the batch normalization (BN) layer is added in front of the activation function of each hidden layer, and the Relu activation function is used for the final output layer; third, spectral angular distance ( LSAD) is used as the objective function instead of the mean square error ( LMSE). The proposed model obtained the parameters by optimizing the objective function through gradient descent method. Then, two simulation datasets with different mineral combinations and different mass fractions are established by using the Hapke model. The datasets include ten pure minerals, kaolinite, pyrophyllite, montmorillonite, chlorite, muscovite, calcite, hematite, dolomite, potassium feldspar and limonite. Finally, SSAE method is used to test the datasets. Test results of SSAE are compared with the results of six cases in the process of autoencoder network improvement as well as the results of VCA and SISAL. Experiments show that the accuracy of SSAE endmember extraction is greatly improved than before. The SSAE method can successfully identify all endmembers of two data sets. The mean errors of Spectral Angle Distance(SAD) are respectively 0.059 7 and 0.034 4, which is less different from the result of the VCA and is better than there sult of SISAL. SSAE method provides a new ideal for hyperspectral unmixing, and has a better promoting effect on the geological application and quantitative analysis of hyperspectral remote sensing.

Keyword: Stacked sparse autoencoders; Neutral network; Endmember extraction; Hyperspectral; Mineral
引言

岩石高光谱解混是岩矿光谱定量分析的关键技术, 也是连接遥感与传统地质的关键[1], 对于矿产资源勘查以及遥感地质探测等都具有重要意义。 岩石高光谱是若干组分矿物的综合反映, 正确的端元识别和丰度提取成为了岩石高光谱解混的主要研究任务。 丰度提取精度往往依赖于端元的组合方式[2]和端元识别的准确性[3], 因此正确提取矿物端元是高光谱解混的关键技术。

为了解决高光谱解混的难题, 学者们提出了众多算法, 基本可以分为基于模型驱动算法和基于数据驱动算法两类。 模型驱动算法一般是基于线性、 非线性或混合模型展开的, 在确定具体模型的基础上求解目标参数。 模型驱动算法又可以分为基于纯像元的端元提取算法和基于无纯像元的端元生成算法。 VCA[4]是基于纯像元假设的较常用的端元识别算法, 通过选择最大单形体体积确定端元, 将像元在所有维度进行投影, 把投影值最大的像元作为第一个端元, 再把高光谱数据投影到与已确定端元构成的子空间正交方向上, 通过迭代法选取其他端元。 SISAL[5]是基于最小体积的方法通过寻找将高光谱数据完全包围的最小体积的单形体提取端元, 不受数据集中是否存在纯像元的约束。 传统的端元提取算法通过几何或者统计学的假设在高光谱解混方面表现出较好的性能, 在过去的二十年中一直受广大学者青睐, 然而基于纯数学的方法往往忽视数据的空间特征, 数据集中噪声的存在容易造成不正确的初始化等问题限制了这些方法的提取效果, 除此之外端元提取精度对混合像元数量、 噪声干扰、 特征选取等依赖性较大[6]。

基于数据驱动的方法为岩石高光谱解混提供了新的解决方案。 神经网络可以处理复杂的非线性问题, 已经成功应用于高光谱影像分类[7]和一些典型高光谱影像解混[8, 9], 由于带有标签影像数据集的缺乏, 在真实影像解混方面的应用依然较少。 近年来, Palsson等基于改进的神经网络自编码的方法执行盲解混, 测定不同的激活函数和目标函数在解混方面的性能, 并证明该方法对高光谱解混具有较强的鲁棒性[10]; Savas等也证明神经网络模型适用于高光谱解混, 在Urban, Samson, Jasper Ridge和Cuprite数据集解混方面取得了重要进展[11]。 深层神经网络由于其强大的特征提取功能在高光谱解混方面表现出较好的优势, 但由于样本量的影响目前在矿物高光谱解混方面的实验依然较为缺乏。

依据深度神经网络原理, 针对传统浅层神经网络特征提取不足、 神经网络过拟合以及局部最优等问题对堆栈稀疏自编码结构进行改进, 不断对隐藏层层数和和隐藏层的节点数进行调试, 通过删除bias项, 在隐藏层激活函数之前添加BN层以及修改目标函数等方面做出改进, 提出了一种可以进行盲端元识别的SSAE方法, 该方法不受数据集中是否存在纯矿物的限制, 也不受数据是线性混合还是非线性混合的约束。 用于测试的数据集是通过Hapke模型模拟构建的, 不受样本量的影响, 并添加了30 dB的高斯白噪声, 使其更接近真实影像数据。

1 自编码结构及改进
1.1 自编码基本结构

自编码是一种无监督的前馈神经网络, 通过学习特定的函数使输出信号无限的逼近输入。 自编码结构主要包括两个部分, 即编码过程(encoder)和解码过程(decoder)。

y=fwe·x+beencoder(1)

$\hat{\boldsymbol{x}}=f\left(\boldsymbol{w}^{d} \cdot \boldsymbol{y}+b^{d}\right) \operatorname{decoder}$ (2)

式中, x为原始输入光谱矩阵, x˙为输出光谱矩阵; we和wd分别表示编码和解码过程的权重矩阵, be和bd分别表示bias项; f(· )为激活函数, 常用的激活函数有sigmoid, tanh和Relu等, 其中· 表示内积。 在自编码神经网络结构中输入层与输出层节点数相同, 稀疏自编码最大特征是隐藏层的节点数小于输入层与输出层, 在训练过程中通过目标函数使输出光谱无限逼近于输入光谱。 堆栈稀疏自编码神经网络是由多层稀疏自编码器组成的神经网络, 其前一层自编码器的输出作为其后一层自编码器的输入, 每一层单独进行训练。

1.2 自编码结构的改进

堆栈自编码网络具有较强的特征提取能力, 设置网络结构包括输入层、 两个隐藏层和输出层, 输入和输出层的节点数均为光谱波段数。 隐藏层节点数、 学习率、 迭代次数、 稀疏惩罚等参数的设置都会对端元提取结果产生影响, 需要不断进行调试确定。 为了可以更好的识别矿物端元, 对堆栈稀疏自编码神经网络结构主要做了3点改进。

(1)去掉bias项

在回归或者分类功能的神经网络中, bias项具有重要的作用, 通过对激活函数的响应影响下一层网络参数。 但在端元提取网络中, bias项犹如额外的端元光谱对端元提取的精度产生负面影响, 因此尝试将bias项去掉。

(2)隐藏层激活函数之前添加BN层

SSAE网络使用sigmoid作为隐藏层的激活函数, 在激活函数之前添加BN层。 在神经网络训练中, 随着深度的增加, 输入值的分布会发生偏置, 在反向传播过程中容易导致低层神经网络梯度消失。 添加BN层后, 通过一定的规范手段, 将神经网络输入值的分布强行拉回到均值为0、 方差为1的标准正态分布, 使得每层输入数据的分布相对稳定, 加速模型学习, 模型对网络中的参数敏感性减弱, 从而简化了网络调参的过程, 以sigmoid为激活函数解决了梯度消失问题。 BN层公式如下

$\hat{a}_{i}^{l+1}=\mathrm{BN}\left(\hat{a}_{i}^{l}\right)=\hat{\gamma a}_{i}^{l}+\beta$ (3)

$\hat{a}_{i}^{l}=\frac{a_{i}^{l}-\mu}{\sqrt{\sigma^{2}+\varepsilon}}$ (4)

μ=1n∑i=1nail(5)

σ2=1n∑i=1n(ail-μ)2(6)

其中 a˙il表示第l层的输入, i=1, …, n表示由前一层传递下来的数值量, μ 为ai的均值, σ 2为ai的方差, γ 和β 为网络的训练参数, ε 为非常小的常数项。

(3)设置目标函数为LSAD

目标函数是用来度量神经网络输入与输出差异的函数, 通过梯度下降算法不断对目标函数进行优化, 从而获取网络参数。 多数神经网络使用LMSE作为目标函数, 本研究通过实验验证, 最终选择LSAD作为目标函数。 式(7)和式(8)中x表示输入数据集, x˙表示神经网络最后一层的输出的重建光谱, p=1, …, P, P为光谱样本数量。

$L_{\mathrm{MSE}}=\frac{1}{p} \sum_{p}^{P}\|\hat{x}-x\|_{2}^{2}$ (7)

$L_{\mathrm{SAD}}=\frac{1}{p} \sum_{p}^{P} \arccos \left(\frac{(\hat{x}, x)}{\|\hat{x}\|_{2}\|x\|_{2}}\right)$ (8)

除了上述改进之外, 还对第一层的自编码结构添加denoising, 即对第一层的输入数据添加噪声, 以0.5的概率分布去擦除原始输入的数据矩阵并将其设置为0, 然后对丢失部分特征的数据继续进行运算, 增加了模型的泛化能力。 改进后的SSAE网络结构见图1, 隐藏层使用sigmoid激活函数, 最后一层隐藏层到输出层使用Relu激活函数, 最后一层隐藏层到输出层的权值w(L)即为矿物端元光谱。 在精度测试中以SAD作为误差检测标准, SAD表征提取的端元光谱w(L)与实验室实测端元光谱之间的反余弦值, 取值范围为[0, Π ], 取值越小说明两条光谱越相似, 端元识别结果越准确。

图1 改进的堆栈稀疏自编码网络结构Fig.1 Improved stacked sparse autoencoders network structure

2 实验数据集
2.1 数据集生成步骤

Hapke模型可以较好的描述矿物的混合效应, 已经在矿物非线性混合方面取得较好成果[12, 13]。 本研究基于Hapke模型创建了混合矿物样本库, 解决了基于数据驱动的神经网络在进行实验时需要大量数据的问题和精度验证问题。 模拟数据集生成步骤如下:

(1)获得端元光谱。 使用美国ASD FieldSpecFR Pro便携式光谱仪在实验室获得高岭石、 叶腊石、 蒙脱石、 绿泥石、 白云母、 方解石、 赤铁矿、 白云石、 钾长石和褐铁矿10种纯净矿物粉末光谱, 光谱范围为350~2 500 nm, 数据间隔1 nm, 选取2 000~2 400 nm波段的数值采样至80个波段。

(2)计算纯净端元矿物单次散射反照率。 利用Hapke模型分别计算10种矿物端元的单次散射反照率。 入射角为40° , 出射角为0° , 单次散射反照率表征一束光线照射到单个矿物颗粒表面散射能量与入射能量之比, 呈线性混合规律。

ωm=1-(μ0+μ)2xm2+(1+4μ0μxm)(1-xm)-μ0+μxm1+4μ0μxm2(9)

其中, ω m为第m种矿物的单次散射反照率, m=1, …, 10, μ 0为入射角余弦值, μ 为出射角余弦值, xm表示第m种矿物的光谱反射率。

(3)生成“ 和为一” 的混合矩阵。 在matlab中随机生成二元、 三元和四元组合的“ 和为一” 的丰度矩阵em。

(4)生成单次散射反照率混合矩阵。 将纯净矿物的单次散射反照率ω m与随机生成的矩阵em进行线性组合, 生成混合光谱单次散射反照率ω 矩阵。 M表示模拟数据集端元总数, ε 表示误差。

ω=∑m=1Memωm+ε(10)

(5)生成混合光谱数据集。 将计算得到的混合光谱单次散射反照率ω 转换为混合光谱反射率, 得到模拟的混合光谱数据集x。

x=14(μ0+μ)1(1+2μ1-ω)(1+2μ01-ω)(11)

(6)为使模拟数据更接近于原始影像数据, 为模拟数据集添加30 dB的高斯白噪声。

2.2 模拟数据集设置

利用上述方法分别对选取的10种纯净矿物光谱进行两元、 三元、 四元混合制样, 生成两个混合光谱数据集: 数据集一和数据集二, 端元数目设置为5, 混合配置见表1和表2。

表1 模拟数据集一 Table 1 Simulation dataset one
表2 模拟数据集二 Table 2 Simulation dataset two
3 结果与讨论

虽然矿物具有其特有的光谱属性, 但有些矿物光谱在可见光-近红外波段具有相似性, 有些矿物光谱变化幅度不显著, 如钾长石、 褐铁矿等在2 000~2 400 nm范围内光谱特征十分平缓, 钾长石和石英等在2 000~2 400 nm的波长范围内光谱相似度较高, 这些光谱特征都增加了端元识别的难度。 除此之外, 数据中包含的端元数目越多, 噪声干扰越大, 端元识别难度也会变大。

改进之后的SSAE(BN+LSAD)神经网络以LSAD为目标函数、 添加BN层、 删除bias项; 原始的自编码网络结构简写为LMSE+bias, 即以LMSE为目标函数、 保留bias项。 为验证改进后SSAE方法的优势, 以数据集一的端元提取结果为例, 对改进过程中产生的6种情况进行测试, 分别为: LMSE(在原始结构上删除bias项)、 LSAD+bias(修改原始自编码的目标函数为LSAD)、 LSAD(修改目标函数为LSAD, 删除bias项)、 BN+LMSE+bias(在原始结构上添加BN层)、 BN+LMSE(原始结构添加BN层, 删除bias项)、 BN+LSAD+bias(原始结构添加BN层, 修改目标函数为LSAD)。 在对所有数据集进行测试时, 每种方法运行10次, 取10次运行结果的平均值。

改进过程中产生的6种情况测试结果见表3, 原始的神经网络结构仅删除bias项(LMSE)或者只添加BN层(BN+LMSE+bias)都不能正确的识别矿物端元; 在添加BN层并且删除bias项(BN+LMSE)后, 可以正确的识别白云母和绿泥石, 但绿泥石的识别精度超过了0.100 0。 修改目标函数为LSAD后, 无论保留bias项(LSAD+bias)或者删除bias项(LSAD)都不能正确识别矿物端元; 但在添加BN层(BN+LSAD+bias)的情况下可以较好的识别蒙脱石和高岭石, 识别误差分别为0.095 1和0.048 5, 平均误差精度为0.108 1。

表3 自编码改进过程中6种情况识别结果 Table 3 Results based on six conditions in the improvement of autoencoder

利用改进后的SSAE(BN+LSAD)方法对数据集一进行测试, 结果见表4。 改进后的SSAE可以成功识别5种矿物端元, 对数据集一端元提取的平均误差为0.059 7, 相较于改进过程中的6种情况, 提取精度有了显著提升。 由表4可知, VCA, SISAL和SSAE三种方法均可以识别数据集一中的5种矿物端元, 平均识别精度相差较小。 SSAE的平均误差略低于VCA法的平均识别误差0.041 3, 优于SISAL法的平均识别结果0.073 9。 SISAL法对高岭石和绿泥石的识别误差均超过了0.100 0, 相比较而言, SSAE法对5种矿物识别精度较均匀。

表4 数据集一: 不同方法端元提取精度比较 Table 4 Dataset 1: comparison of end member extraction accuracy of different methods

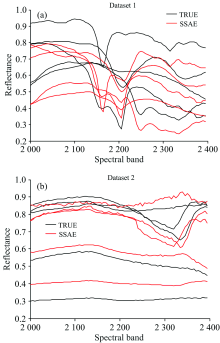
利用改进后的SSAE方法继续对数据集二进行端元识别测试并与VCA和SISAL进行比较(表5)。 SSAE方法依然可以较精确的识别5种矿物端元, 平均误差为0.034 4, 对5种矿物的识别误差均较小; VCA方法获得的平均识别误差为0.034 0, 对褐铁矿的识别误差为0.065 2, 明显差于SSAE法; SISAL方法对数据集二的识别结果最差, 平均误差为0.525 9, 钾长石的识别误差相对较大为0.126 2, SISAL方法不能正确的识别褐铁矿。 SSAE对两个模拟数据集10种矿物的识别结果相对较稳定, 端元提取结果直观图见图2, SSAE方法可以较好的从混合数据集中识别矿物端元, 提取光谱与纯矿物光谱的相似度较好。

表5 数据集二: 不同方法端元提取精度比较 Table 5 Dataset 2: comparison of end member extraction accuracy of different methods

图2 SSAE法端元提取结果Fig.2 End member extraction results of SSAE

针对岩石高光谱解混问题, 提出了一种改进的堆栈稀疏自编码端元识别方法。 对原始自编码结构进行3点主要改进: 删除bias项, 添加BN层以及设置目标函数为LSAD, 通过不断测试隐藏层层数和节点数等构建了可以进行端元识别的深度神经网络SSAE。 利用Hapke模型建立两个模拟数据集对该方法进行测试, 结果证明SSAE方法可以成功的识别两个数据集全部的矿物端元, 在端元识别方面具有较高的准确性和稳定性, 端元识别精度与改进之前具有显著提升, 与传统的VCA和SISAL方法相比也具有较好的优势。 SSAE方法为岩石高光谱解混提供了新的研究方向。

也还存在一些问题有待进一步探究。 不论是VCA、 SISAL还是SSAE方法都需要提供明确的端元数目值, 端元总数目的正确估计对端元光谱能否正确提取具有直接的影响。 本研究仅用了模拟数据进行端元光谱提取来验证SSAE方法的可靠性, 今后还需要在真实高光谱数据端元提取方面进行验证。 由于真实高光谱数据量远远大于模拟数据量, 利用深度神经网络进行端元识别的效率会受到计算机性能的制约, 因此利用GPU计算将会是未来在高光谱影像解混方面的重点研究内容。

参考文献
[1] ZHANG Cheng-ye, QIN Qi-ming, CHEN Li, et al(张成业, 秦其明, 陈理, 等). Optics and Precision Engineering(光学精密工程), 2015, 23(8): 2407 [本文引用:1]
[2] ZHAO Heng-qian, ZHANG Li-fu, WU Tai-xia, et al(赵恒谦, 张立福, 吴太夏, 等). Spectroscopy and Spectral Analysis(光谱学与光谱分析), 2013, 33(1): 172. [本文引用:1]
[3] Bioucas-Dias J M, Plaza A, Dobigen N, et al. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2012, 5(2): 354. [本文引用:1]
[4] Nascimento J M P, Bioucas-Dias J M. IEEE Transactions on Geoscience and Remote Sensing, 2005, 43(4): 898. [本文引用:1]
[5] Miao L, Qi H. IEEE Transactions on Geoscience and Remote Sensing, 2007, 45(3): 765. [本文引用:1]
[6] Bioucas-Dias J M, Plaza A, Dobigeon N, et al. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2012, 5(2): 354. [本文引用:1]
[7] Ratle F, Camps-Valls G, Weston J. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(5): 2271. [本文引用:1]
[8] Licciardi G A, Del Frate F. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(11): 4163. [本文引用:1]
[9] Yuan-Chao S, Andrea M, Jun L, et al. IEEE Geoscience and Remote Sensing Letters, 2018, 15(9): 1427. [本文引用:1]
[10] Palsson B, Sigurdsson J, Sveinsson J R, et al. IEEE Access, 2018, 6: 25646. [本文引用:1]
[11] Ozkan S, Kaya B, Akar G. IEEE Transactions on Geoscience and Remote Sensing, 2019, 57(1): 482. [本文引用:1]
[12] WANG Zhe, ZHAO Zhe, YAN Bai-kun, et al(王喆, 赵哲, 闫柏琨, 等). Remote Sensing for Land and Resources(国土资源遥感), 2017, 29(1): 186. [本文引用:1]
[13] Heylen R, Gader P. IEEE Geoscience and Remote Sensing Letters, 2014, 11(7): 1195. [本文引用:1]