低偶然符合效应的高脉冲分辨能力数字化X荧光能谱仪研制

引用本文

王忠桃, 何黎, 胡传皓, 白彬, 顾民, 曾国强, 葛良全, 严磊, 杨寿南. 低偶然符合效应的高脉冲分辨能力数字化X荧光能谱仪研制[J]. 光谱学与光谱分析, 2021,41(3): 768-775.
WANG Zhong-tao, HE Li, HU Chuan-hao, BAI Bin, GU Min, ZENG Guo-qiang, GE Liang-quan, YAN Lei, YANG Shou-nan. Development of Digital X-Ray Fluorescence Spectrometer With Low Accidental Coincidence Effect[J]. Spectroscopy and Spectral Analysis, 2021,41(3): 768-775.
Doi:10.3964/j.issn.1000-0593(2021)03-0768-08 复制到剪切板

Permissions

《光谱学与光谱分析》期刊社所有

低偶然符合效应的高脉冲分辨能力数字化X荧光能谱仪研制

王忠桃, 何黎, 胡传皓, 白彬, 顾民, 曾国强^*, 葛良全, 严磊, 杨寿南

成都理工大学地学核技术四川重点实验室, 四川成都 610059

*通讯作者 e-mail: zgq@cdut.edu.cn

作者简介: 王忠桃, 1979年生, 成都理工大学地学核技术四川重点实验室讲师 e-mail: wzt@cdut.edu.cn

收稿日期: 2019-12-31 修订日期: 2020-03-18

基金: 国家(863)计划项目(2017YFC0602101)资助

摘要

在X荧光能谱测量中, 当两个事例发生间隔较短时, 存在脉冲前沿或后沿堆积的情况。如果能谱仪的脉冲分辨能力不足, 在事例发生间隔小于能谱仪脉冲分辨能力时, 发生了偶然符合效应。当堆积发生在信号的上升沿时, 后端电子学无法识别堆积脉冲, 并将堆积脉冲当成1个脉冲, 从而在测量能谱中会产生虚假能峰; 当堆积出现在下降沿时, 堆积信号间隔小于通道成形时间时, 堆积信号会被丢弃, 导致所测量谱线的有效计数减小, 对精确放射性测量带来了不利影响。从提高能谱仪模拟电路信噪比、降低误触发、缩短快成形通道成形时间、提高能谱仪的脉冲分辨能力, 从而减小符合效应等角度入手, 研制了一种低偶然符合效应的快慢双成形通道的数字化能谱仪。该能谱仪设计了具有高脉冲分辨能力的快通道, 采用对称零面积梯形成形算法, 有效消除快通道时间变窄带来的不足, 结合对梯形平顶的判断, 实现对低频噪声抑制与降低误触发概率; 同时设计高信噪比、低噪声的模拟电路以减小快通道对噪声误触发的概率, 降低偶然符合概率。文中先利用仿真验证了提升快通道时间可以提升脉冲分辨能力, 接着利用MOXTEK的X光管激发被测样品Cu获得特征X射线, 由KETEK的高分辨率SDD探测器检测信号, 通过调节X光管的管流得到计数率范围为13~103 kcps的X荧光能谱, 从而得到偶然符合概率与计数率的关系, 并且通过改变快通道成形时间分析其对偶然符合的影响。实验表明, 更低的快通道成形时间拥有更高的脉冲分辨率能力, 更低的偶然符合效应; 在103 kcps计数率下, 150 ns快通道成形时间条件下, Cu的 Kα峰、 Kβ及 Kα+ Kβ的偶然符合概率分别为1.568%, 0.265%和0.403%; 设计的对比实验结果表明: 在相同快通道成形时间条件下, 所研制的数字化能谱仪相比于Amptek的DP-5型号数字化能谱仪偶然符合概率低了60%。

关键词: 偶然符合效应; 快慢成形通道; 脉冲分辨能力; 对称零面积梯形成形

中图分类号:TL817+.1 文献标志码:A

Development of Digital X-Ray Fluorescence Spectrometer With Low Accidental Coincidence Effect

WANG Zhong-tao, HE Li, HU Chuan-hao, BAI Bin, GU Min, ZENG Guo-qiang^*, GE Liang-quan, YAN Lei, YANG Shou-nan

College of Nuclear Technology and Automation Engineering, Chengdu University of Technology, Chengdu 610059, China

*Corresponding author

Abstract

In the measurement of the X-ray fluorescence spectrum, when the interval between the two cases is short, there is a rising or falling edge pulse pile-up. If the pulse resolution of the spectrometer is not enough, the accidental coincidence effect occurs when the event interval is less than the pulse resolution of the spectrometer. When the pulse pile-up occurs on the rising edge of the signal, the next stage electronics is hard to identify the pile-up pulses and regards them as a single pulse, leading to the coincidence peaks and incorrect spectrum measurement. When the pulse pile-up appears at the falling edge, and the pile-up pulse interval is shorter than the digital shaping time of the multichannel pulse amplitude analyzer, the pile-up pulse will be discarded and lead to the reduction of spectrum count and cause a low throughput rate, which has a negative effect on the precision of radioactivity measurement. In this paper, increasing the signal-to-noise ratio of the analog circuit, reducing the false trigger and shortening the forming time of the fast forming channel, so as to improve the pulse resolution ability of the spectrometer and reduce the coincidence effect, a digital spectrometer of the fast and slow dual forming channel with low accidental coincidence effect is developed. The energy spectrometer has designed a fast channel with high pulse resolution. Based on the symmetrical zero area trapezoid forming algorithm, it can effectively eliminate the shortcomings caused by the narrowing of fast channel time, combined with the judgment of the trapezoidal flat top, the low-frequency noise suppression and error reduction are realized trigger probability. At the same time, the analog circuit with high signal-to-noise ratio and low noise is designed to reduce the probability of false noise triggering and an accidental coincidence of fast channel. In this paper, firstly, the fast channel time enhancement ability is verified by simulation, and then Cu samples were excited through the X-ray tube created by Moxtek to obtain characteristic X-rays, and the signal is detected by the high-resolution SDD detector of KETEK. The tube current of the X-ray tube was adjusted to acquire X-ray fluorescence spectra with a count rate ranging from 13 to 103 kcps and determine the relationship between the probability of accidental coincidence and count rate. Then, the influence of the shaping time change of the fast channel on accidental coincidence was analyzed. Experiments showed that a short fast-channel shaping time resulted in high pulse pair resolution and low accidental coincidence effect. At a 103 kcps count rate, under the fast-channel shaping time of 150 ns, the accidental coincidence probabilities of the Kα, Kβ, and Kα+Kβ combination peaks of Cu were 1.568%, 0.265%, and 0.403%, respectively. Under the same fast-channel shaping time, the accidental coincidence probability of the proposed digitized digital spectrometer was 60% lower than that of the DP-5 digital spectrometer produced by Amptek.

Keyword: Accidental coincidence effect; Fast-slow digital shaper; Pulse pair resolution; Symmetrical zero-area trapezoidal shaping

文章图片

引言

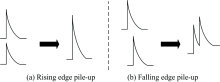
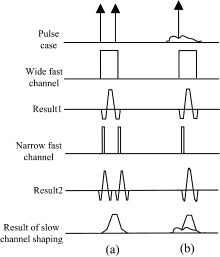
由于核事例发生的随机性, 因此同时发生或者短时间内相继发生核事例都存在一定的概率。核探测器输出的电流脉冲通过前置放大器等后得到具有快指数上升沿和慢指数衰减特征的电压脉冲信号, 当衰减时间较长时, 发生脉冲堆积的概率变大; 当两个事例发生间隔较短时, 存在脉冲前沿\后沿堆积的情况, 而由于能谱仪的脉冲分辨能力不足, 在事例发生间隔小于能谱仪脉冲分辨能力时, 发生堆积的多个事例将被处理为1个事例, 发生了偶然符合效应, 从而在测量能谱中出现了合峰情况, 产生了虚假能峰, 对精确放射性测量带来了不利影响^{[1, 2]}。图1展示了两种脉冲堆积的方式, 前沿堆积容易将到来时间很近的两个脉冲积合成单个脉冲, 产生偶然符合效应, 会计数错误以及造成谱线出现假峰, 如图1(a)所示。后沿堆积导致在数字化多道中堆积脉冲被丢弃, 使脉冲通过率下降, 同时导致能谱全能峰展宽, 分辨率降低, 如图1(b)所示。

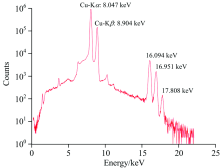
	Figure Option View Download New Window
	图1 两种脉冲堆积方式Fig.1 Two cases of pulse pile-up

具有堆积峰的Cu靶特征X射线谱如图2所示, 被测样品Cu激发了Kα 和Kβ 特征X射线, 由于偶然符合效应, 在谱线700道和850道之间分别产生2倍Kα : 16.094 keV峰, 2倍Kβ : 17.808 keV峰和Kα +Kβ : 16.951 keV三个假峰, 同时后沿堆积导致Kα : 8.047 keV峰和Kβ : 8.904 keV峰全能峰展宽、分辨率下降。此外脉冲堆积会导致基线漂移进而影响能谱分辨率测量准确性、带来峰位漂移等问题, 尤其是在高计数率应用场景下, 脉冲堆积更严重。

	Figure Option View Download New Window
	图2 具有堆积峰的Cu靶特征X射线谱Fig.2 Characteristic X-ray spectrum of Cu target with coincidence peaks

长期以来, 针对脉冲堆积, 中外学者已经进行了大量研究。目前提出的主要方法有相邻脉冲时间间隔比较法^{[3, 4]}、数字脉冲反褶积法^{[5, 6]}、脉冲微分法^[7]、脉冲削波法^[8]、基于Monte Carlo的能谱反卷积算法^[9]、极大似然估计法^[10]等。脉冲微分、脉冲削波以及数字反褶积法都是采用硬件的方式减小脉冲宽度以降低脉冲堆积概率, 提升脉冲分辨能力, 减小脉冲堆积的影响, 能谱反卷积及极大似然估计算法都是采用软件来实现。以上方法都没有从降低能谱仪硬件噪声、提高能谱仪模拟电路信噪比、降低误触发、缩短快成形通道成形时间等角度去提高能谱仪的脉冲分辨能力, 从而减小符合效应等开展研究, 因此并不能从本质上改善偶然符合现象, 提高能谱准确度和精度。

为精准提取脉冲信息, 数字化能谱仪多采用快、慢双成形通道结构, 较窄的快通道提取脉冲的到达时间信息, 较宽的慢成形通道具有更优的信噪比, 用于提取脉冲幅度信息, 实现较优的能量分辨率^[11]。实验表明, 更窄的快通设计有利于提升对脉冲的时间分辨能力, 进而提升对符合事例的甄别能力, 但快通道时间变窄将使得滤波效果变差, 大大增加快通道误触发的概率, 反而会提高偶然符合概率与系统死时间。与传统的单极性脉冲成形方式比较, 双极性零面积成形能有效抑制基线波动与漂移^[12], 并且结构对称的成形方式能够抑制有色噪声对成形的影响, 故采用对称零面积梯形成形可有效抑制由于快通道成形时间缩短带来的噪声增加, 且其抑制低频噪声效果更加优异, 可减小低频噪声波动带来的误触发。本文研制了一种低偶然符合效应的快慢双成形通道的数字化X荧光能谱仪, 设计具有高脉冲分辨能力的快通道, 采用基于对称零面积梯形成形算法, 有效消除快通道时间变窄带来的不足, 同时设计高信噪比, 低噪声的模拟电路以减小快通道对噪声误触发的概率, 试验验证了这种谱仪能够有效降低偶然符合效应。

1 实验部分

1.1 整体设计

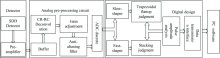
快慢双通道数字化谱仪的整体框架如图3所示, 系统包括探测器部分、前置放大电路、模拟预处理电路以及数字多道脉冲幅度分析器部分。探测器采用KETEK公司的VITUS CUBE型X射线硅漂移探测器, 采用热电致冷技术, 使探头组件工作在零下55 ℃, 降低暗电流噪声, 前置放大器采用KETEK公司VIAMP-KC复位型电荷灵敏放大器^[13]; 模拟预处理部分主要包括CR-RC反褶积、增益调节、 ADC驱动与抗混叠滤波电路、高速ADC离散电路, 模拟电路将脉冲信号调节到ADC线性度较好范围内, 充分利用ADC的动态范围; 本文采用ALTERA公司的EP4CE系列FPGA完成数字多道的设计, 其中包括快、慢双通道滤波成形器、堆积校正、梯形平顶判断、脉冲幅度分析、数据传输接口等模块。其中快通道成形, 其计数作为堆积校正的依据, 慢通道成形用于脉冲信号幅度的提取, 结合梯形平顶判断模块剔除成形结果不符合要求的脉冲信号, 不做幅度提取但对剔除的脉冲个数计数, 并做计数率校正。

	Figure Option View Download New Window
	图3 谱仪整体设计框图Fig.3 Block diagram of the overall design of the spectrometer

1.2 高信噪比模拟预处理电路设计

在核脉冲信号测量中, 提升模拟电路的信噪比有益于幅度提取、谱线能量分辨率等的测量^{[14, 15, 16]}。为减小快通道对噪声误触发的概率, 本文设计低噪声的CR-RC^m滤成形电路, 将前放输出的阶梯上升复位型信号, 滤波成形为具有快上升、慢下降沿的双指数电压信号, 图4是模拟预处理等效电路图。

	Figure Option View Download New Window
	图4 模拟预处理等效电路图Fig.4 Analog preprocessing equivalent circuit diagram

高性能ADC多采用差分输入方式, 可以有效抑制共模噪声和干扰。为获得更佳效果, 本文在模拟预处理部分设计ADC驱动电路实现单端信号到差分的转换, 降低共模噪声的干扰, 同时设计抗混叠滤波电路, 限制模拟电路带宽, 避免ADC过采样。本文采用ADI公司16 bit高速ADC, 其采样率为80MSPS, 为抑制电源噪声串扰至模拟前端电路, 其供电方式均采用高电源纹波抑制比的LDO与π 型LC滤波方式相结合, 使电源噪声小于1 mV, 模拟电路信噪比达到30 dB, 电源噪声及信噪比测试结果如图5(a)和(b)所示。

	Figure Option View Download New Window
	图5 电源噪声及信噪比测试结果图 (a): 模拟电源噪声; (b): 信噪比测试Fig.5 Test results of power supply noise and signal-to-noise ratio (a): Analog power supply noise; (b): Signal-to-noise ratio test

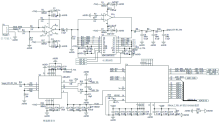
整体的模拟电路设计如图6所示。

	Figure Option View Download New Window
	图6 模拟电路设计Fig.6 Analog circuit design

1.3 快通道对脉冲分辨能力的影响

不同快通道成形时间对事例甄别能力的不同, 如图7所示为快通道成形时间对脉冲成形能力的影响示意图, 图7(a)是不同快通道成形时间对脉冲分辨率的影响示意图, 从图7(a)可知, 快通道成形时间较窄时, 能准确的识别两个时间间隔较近的脉冲事例, 从而能避免偶然符合效应, 当快通道时间较宽时, 无法将两个接近的脉冲有效区分开, 造成合成峰, 无法有效避免偶然符合效应。图7(b)是低频噪声对不同快通道成形时间的影响示意图, 从图7(b)可知, 当快通道时间较宽时, 低频噪声对成形干扰较小, 快通道时间越窄, 低频噪声对成形干扰也越大。

在大量的实验基础上, 综合考虑脉冲分辨能力和降低噪声对成形的干扰等因素, 本系统采用的快通道成形时间最低为150 ns, 最高为900 ns, 并通过实验测试确定最佳值, 并采用对称零面积梯形成形算法降低高低频噪声对事例的干扰和偶然符合。

	Figure Option View Download New Window
	图7 快通道时间对脉冲成形影响示意图Fig.7 Influence of the fast-channel shaping time on pulse shaping

1.4 对称零面积梯形成形算法

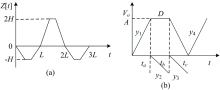
快通道设计采用梯形成形的对称零面积梯形成形算法实现。图8是基于梯形的对称零面积成形示意图。

	Figure Option View Download New Window
	图8 基于梯形的对称零面积成形示意图Fig.8 Symmetrical zero-area shaping diagram based on trapezoids

图8(a)中三个梯形底边及顶边均相等, 正梯形高为负梯形高的两倍, 整个面积之和为零。令图中第一个小梯形的函数为V₀(t), 则利用三个梯形的面积以及位置关系可推导出对称零面积梯形成形的函数表达式

$Z (t) = - V_{0} (t) + 2 V_{0} (t - L) - V_{0} (t - 2 L)$ (1)

图8(b)为分段函数构建小梯形的函数V₀(t)示意图

$\begin{array}{l} V_{o} (t) = \overset{4}{\sum_{i = 1}} y_{i} (t) \\ y_{1} = Au (t) / t_{a} \\ y_{2} = - A (t - t_{a}) u (t - t_{a}) / t_{a} \\ y_{3} = - A (t - t_{b}) u (t - t_{b}) / t_{a} \\ y_{4} = A (1 - t_{c}) u (t - t_{c}) / t_{a} \end{array}$ (2)

其中A为脉冲幅度信息, t_a为梯形的上升沿时间, D为梯形平顶宽度, t_b=t_a+D, t_c=2t_a+D为波形总宽度, u(t)为阶跃函数。

梯形成形算法可以通过传递函数法来实现^[17]。设采样周期为T_s, 令n_a=t_a/T_s, n_b=t_b/T_s, n_c=t_c/T_s, 则对V_o(t)进行Z变换有

$V_{o} (z) = \frac{Az (1 - z^{- n_{a}} - z^{- n_{b}} + z^{- n_{c}})}{n_{a} {(z - 1)}^{2}}$ (3)

探测器输出的核脉冲信号经过CR-RC^m反褶积电路, 滤波成形为双指数信号, 等效电路的输出电压波形表达式如式(4)所示

$V_{i} (t) = A (e^{- t / τ_{1}} - e^{- t / τ_{2}})$ (4)

其中, A为电路增益, τ ₁为晶体发光衰减时间、 τ ₂为等效电路时间常数。

对V_i(t)进行Z变换有

$V_{i} (z) = A (\frac{z}{z - e^{- T_{s} / τ_{1}}} - \frac{z}{z - e^{- T_{s} / τ_{2}}})$ (5)

令e₁= $e^{- T_{s} / τ_{1}}$ , e₂= $e^{- T_{s} / τ_{2}}$ , 则双指数输入信号的梯形成形滤波传递函数为

$\begin{aligned}X(z)=& \frac{V_{o}(z)}{V_{i}(z)}=\left\{1-z^{-n_{a}}-z^{-n_{b}}+z^{-n_{c}}-\left(e_{1}+e_{2}\right)\left(z^{-1}-\right.\right.\\&\left.z^{-\left(n_{a}+1\right)}-z^{-\left(n_{b}+1\right)}+z^{-\left(n_{c}+1\right)}\right)+e_{1} e_{2}\left(z^{-2}-z^{-\left(n_{a}+2\right)}-\right.\\&\left.\left.z^{-\left(n_{b}+2\right)}+z^{-\left(n_{c}+2\right)}\right)\right\} /\left[n_{a}\left(e_{1}+e_{2}\right)\left(1-z^{-1}\right)^{2}\right]\end{aligned}$(6)

结合式(1)和式(6)即可得双指数脉冲信号输入时, 对称零面积梯形成形法的传递函数Z[z]的表达式

$\begin{aligned}Z[z] &=-X[z]+2 X[z-L]-X[z-2 L] \\&=\left\{1-z^{-n_{a}}-z^{-n_{b}}+z^{-n_{c}}-\left(e_{1}+e_{2}\right)\left(z^{-1}-z^{-\left(n_{a}+1\right)}-\right.\right.\\&\left.z^{-\left(n_{b}+1\right)}+z^{-\left(n_{c}+1\right)}\right)+e_{1} e_{2}\left(z^{-2}-z^{-\left(n_{a}+2\right)}-z^{-\left(n_{b}+2\right)}+\right.\\&\left.\left.z^{-\left(n_{c}+2\right)}\right)\right\} /\left[n_{a}\left(e_{1}+e_{2}\right)\left(1-z^{-1}\right)^{2}\right]+2 z^{-L}\left\{1-z^{-n_{a}}-z^{-n_{b}}\right.\\&+z^{-n_{c}}-\left(e_{1}+e_{2}\right)\left(z^{-1}-z^{-\left(n_{a}+1\right)}-z^{-\left(n_{b}+1\right)}+z^{-\left(n_{c}+1\right)}\right)+\\&\left.e_{1} e_{2}\left(z^{-2}-z^{-\left(n_{a}+2\right)}-z^{-\left(n_{b}+2\right)}+z^{-\left(n_{c}+2\right)}\right)\right\} /\left[n_{a}\left(e_{1}+e_{2}\right)(1\right.\\&\left.\left.-z^{-1}\right)^{2}\right]-z^{-2 L}\left\{1-z^{-n_{a}}-z^{-n_{b}}+z^{-n_{c}}-\left(e_{1}+e_{2}\right)\left(z^{-1}-\right.\right.\\&\left.z^{-\left(n_{a}+1\right)}-z^{-\left(n_{b}+1\right)}+z^{-\left(n_{c}+1\right)}\right)+e_{1} e_{2}\left(z^{-2}-z^{-\left(n_{a}+2\right)}-\right.\\&\left.\left.z^{-\left(n_{b}+2\right)}+z^{-\left(n_{c}+2\right)}\right)\right\} /\left[n_{a}\left(e_{1}+e_{2}\right)\left(1-z^{-1}\right)^{2}\right]\end{aligned}$(7)

根据梯形等腰特点以及位置关系可得: L=t_c=2t_a+D, t_b=t_a+D, 化简可得式

$\begin{aligned}&Z[z]=-X[z]+2 X[z-L]-X[z-2 L]\\&=\left[-1+2 z^{-\left(2 n_{a} T_{s}+D\right.}-z^{-2\left(2 n_{a} T_{s}+D\right.}\right]\left(1-z^{-n_{a}}-z^{-n_{b}-D}+\right.\\&\left.\left.z^{-2 n_{c}-D}\right)\left(z^{-1}-e_{1}^{-1}\right)\left(z^{-1}-e_{2}^{-1}\right)\right\} /\left[n_{a}\left(e_{1}+e_{2}\right)\left(1-z^{-1}\right)^{2}\right]\end{aligned}$(8)

对式(8)分析可知: 传递函数存在两个零点: z₀₁=e₁, z₀₂=e₂, 一个重极点: $z_{1, 2}^{p}$ =1。由传递函数知, 对称零面积梯形成形器的滤波效果只与梯形上升时间(n_a)以及平顶时间(D)有关。

滤波成形算法在FPGA中实现逻辑图如图9所示, FPGA具备并行运算、逻辑实现能力强、设计灵活等特点, 根据对称零面积梯形成形算法仿真逻辑结构图, 设计相应的FPGA程序。采样得到的脉冲信号首先放入移位寄存器1中存储, 通过加法器、乘法器以及寄存器等实现算法逻辑结构。

	Figure Option View Download New Window
	图9 快通道成形算法FPGA实现逻辑图Fig.9 FPGA realization logic diagram of fast-channel shaping algorithm

2 结果与讨论

2.1 快通道脉冲分辨能力

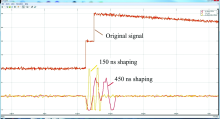
对不同成形时间的快通道对堆积脉冲的分辨率能力不同, 论文对其开展了仿真验证, 原始波形数据通过JTAG获取FPGA与ADC采集到的真实核脉冲信号, 快通道不同成形时间的仿真结果如图10所示, 从图中可以看出当原始信号产生堆积时, 较窄的150ns快通道成形波形完整, 能区分堆叠的脉冲信号, 而450 ns宽快通成形时间成形结果畸形, 不能有效识别脉冲个数, 仿真验证了提升快通道时间可以提升脉冲分辨能力。

	Figure Option View Download New Window
	图10 不同快通道时间成形效果Fig.10 Shaping results of the different fast-channel shaping times

2.2 快通道成形时间与偶然符合效应

为了分析快通道成形时间与偶然符合效应的关系, 在不同计数率的情况下测试了不同快通道成形时间的偶然符合概率。实验测试系统包括探测器、数字化多道谱仪以及PC上位机三部分, X射线由MOXTEK的50 kV Monoblock X射线源(TUB00083-AG1)激发, Cu的特征X射线的能量由KETEK的SDD检测器(有效面积: 20 mm²)检测到。上位机测控软件可控制X射线管管流, 达到不同计数率测试目的。为使得峰总比与计数率较好的平衡, 取入射角为45° 、出射角为75° , 即X射线管与样品平面夹角45° , SDD探头与样品平面夹角15° 。为降低统计涨落对实验结果的影响, 实验采取多次定时测量的方法, 每组数据测量3次, 每次测量10 min。

在不同计数率、测试的偶然符合概率如表1所示。

表1 不同计数率、快通道时间下偶然符合概率 Table 1 Accidental coincidence probabilities vs. different count rate and fast-channel time

表1中偶然符合概率定义为

$K = \frac{N}{M}$ (9)

式(9)中, K表示偶然符合概率, N为由于特征峰偶然符合效应形成假峰的全能峰(fullenergy peak)左右0.4 keV能量范围谱记数, M为特征峰全能峰左右0.4 keV能量范围谱计数。

表1结果表明: 偶然符合概率随计数率增加而增加, 说明脉冲堆积引起的合峰效应增加。偶然符合概率随快通道时间减少而减小, 说明减少快通道的时间在不同的计数率情况下都可以明显降低偶然符合效应。

2.3 两种谱仪在不同计数率下符合效应对比

为了研究本文设计的快慢双通道数字化谱仪与传统的数字化谱仪偶然符合效应的对比, 设计了两种谱仪在不同计数率下的对比测试实验。传统的数字化谱仪采用AMPTEK公司DP5脉冲幅度分析器, 其快通道成形峰值保持时间最短为50 ns, 本文设计的数字化谱仪快通道采用150 ns。在实验中逐步增大X光管电流, 使样品被激发出更多的特征X射线, 在不同计数率下观察两种谱仪偶然符合效应的情况。图11是同一计数率情况下两种谱仪的谱线结果, 本设计谱仪的Kα 峰计数明显比DP5低。

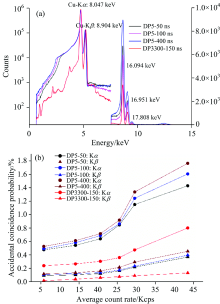	Figure Option View Download New Window
	图11 对比测试图 (a): 谱线图; (b): 偶然符合率Fig.11 Result of the comparative test (a): Spectrum line; (b): Coincidence rate

如图11(a)所示, 我们使用两种数字化谱仪测量了样品的特征X射线光谱。结果表明, 两种光谱仪测得的特征Kα 和Kβ 射线的计数相同, 但符合峰计数DP5的测量结果明显高于我们的设计, 偶然的符合效应更为严重。此外, 低能段中的DP5计数太高, 我们设计的光谱仪在低能段中出现了几个可能的特征峰。我们认为有以下几种原因: (1)高信噪比模拟电路为测量低能射线提供了基本条件, 同时降低了谱线的峰本比。 (2)高脉冲对分辨率与波形判别算法可以更有效地识别低能射线和噪声, 减少噪声对低能射线检测的影响。 (3)测量样品中可能含有某些杂质。具体偶然符合率如图11(b)所示, 从图11(b)中可看出, 在不同的计数率的情况下, 本文设计的快慢双通道数字化谱仪比传统的数字化谱仪具有更低的偶然符合概率, 其原因是本文设计的谱仪采用了低噪声模拟电路设计以及对称零面积梯形成形方法。当本文设计的谱仪采用150 ns的快通道时间分辨率的情况下, 实验结果表明偶然符合概率均比DP5测量结果低。通过对比试验可知, 本文设计的谱仪是一种低偶然符合效应的快慢双通道数字化谱仪。

3 结论

偶然符合效应对核脉冲能谱的测量带来误差, 尤其是在高计数率情况下更严重。减少快通道的时间分辨率可以降低偶然符合效应, 但会增大噪声对快通道成形的干扰。本文在研究了快通道时间对偶然符合效应的影响的基础上, 研制了一种低偶然符合效应的快慢双通道数字化谱仪, 快通道时间分辨率选择150 ns, 通过设计高信噪比模拟预处理电路以及采用对称零面积梯形成形降低了噪声对快通道成形的干扰。通过与传统数字化谱仪在不同计数率情况下偶然符合概率实验的对比, 验证了本文设计的快慢双通道数字化谱仪具有较低偶然符合效应。

参考文献

文献列表

[1]	Taguchi K, Frey E C, et al. Medical Physics, 2010 37(8): 3957. [本文引用:1]
[2]	ZHANG Huai-qiang, WU He-xi, TANG Bin, et al(张怀强, 吴和喜, 汤彬, 等). Journal of East China Institute of Technology·Natural Science Edition(东华理工大学学报·自然科学版), 2012, 35(3): 281. [本文引用:1]
[3]	CHEN Hong-xi, PANG Xi-shun, WANG Hui, et al(陈红喜, 庞希顺, 王辉, 等). Nuclear Electronics & Detection Technology(核电子学与探测技术), 2014, 34(4): 485. [本文引用:1]
[4]	ZENG Guo-qiang, YANG Jian, OUYANG Xiao-ping, et al(曾国强, 杨剑, 欧阳晓平, 等). Atomic Energy Science and Technology(原子能科学技术), 2017, 51(9): 1671. [本文引用:1]
[5]	Valentin T Jordanov. Nuclear Instruments and Methods in Physics Research Section A, 2016, 805: 63. [本文引用:1]
[6]	LUO Xiao-liang, JIANG Xin-biao, ZHANG Wen-shou, et al(罗晓亮, 江新标, 张文首, 等). Atomic Energy Science and Technology(原子能科学技术), 2017, 51(8): 1478. [本文引用:1]
[7]	Bolic M, Drndarevic V. Instrumentation & Measurement Technology Conference. IEEE, 2008. [本文引用:1]
[8]	Liu Zhenzhou, Chen Jinxiang. Measurement Science and Technology, 2008, 19(8): 085102. [本文引用:1]
[9]	Bolic M, Drndarevic V, Gueaieb W. IEEE Transactions on Instrumentation and Measurement, 2010, 59(1): 122. [本文引用:1]
[10]	HUANG Yu-yan, GONG Hui, LI Jian-min(黄宇雁, 宫辉, 李荐民). Journal of Tsinghua University·Science and Technology(清华大学学报·自然科学版), 2017, 57(5): 521. [本文引用:1]
[11]	Zeng Guoqiang, Yang Jian, Hu Tianyu, et al. Nuclear Instruments and Methods in Physics Research Section A, 2017, 858: 57. [本文引用:1]
[12]	Regadío A, Tabero J, Sánchez-Prieto S. Nuclear Instruments and Methods Phys. Res. A, 2016, 811: 25. [本文引用:1]
[13]	GAO Hong-xia, WU Li-xuan, XU Han, et al(高红霞, 吴丽璇, 徐寒, 等). Optics and Precision Engineering(光学精密工程), 2014, 22(11): 3100. [本文引用:1]
[14]	LIANG Chuan-hui, WANG Yu-dan, DU Guo-hao, et al(梁传晖, 王玉丹, 杜国浩, 等). Acta Optica Sinica(光学学报), 2015, 35(3): 310003. [本文引用:1]
[15]	HUANG Jian-heng, DU Yang, LEI Yao-hu, et al(黄建衡, 杜杨, 雷耀虎, 等). Acta Phys. Sin. (物理学报), 2014, 63(16): 168702. [本文引用:1]
[16]	Imperiale C, Imperiale A. Measurement, 2001, 30(1): 49. [本文引用:1]
[17]	LAN Xu-ying, HE Shang-ming, ZHENG Yi, et al(兰旭颖, 何上明, 郑怡, 等). Spectroscopy and Spectral Analysis(光谱学与光谱分析), 2019, 39(9): 2794. [本文引用:1]

2010

0.0

... 当两个事例发生间隔较短时, 存在脉冲前沿\后沿堆积的情况, 而由于能谱仪的脉冲分辨能力不足, 在事例发生间隔小于能谱仪脉冲分辨能力时, 发生堆积的多个事例将被处理为1个事例, 发生了偶然符合效应, 从而在测量能谱中出现了合峰情况, 产生了虚假能峰, 对精确放射性测量带来了不利影响^[1,2] ...

2012

0.0

2014

0.0

... 目前提出的主要方法有相邻脉冲时间间隔比较法^[3,4]、数字脉冲反褶积法^[5,6]、脉冲微分法^[7]、脉冲削波法^[8]、基于Monte Carlo的能谱反卷积算法^[9]、极大似然估计法^[10]等 ...

2017

0.0

2016

0.0

2017

0.0

2008

0.0

2008

0.0

2010

0.0

2017

0.0

2017

0.0

... 为精准提取脉冲信息, 数字化能谱仪多采用快、慢双成形通道结构, 较窄的快通道提取脉冲的到达时间信息, 较宽的慢成形通道具有更优的信噪比, 用于提取脉冲幅度信息, 实现较优的能量分辨率^[11] ...

2016

0.0

... 与传统的单极性脉冲成形方式比较, 双极性零面积成形能有效抑制基线波动与漂移^[12], 并且结构对称的成形方式能够抑制有色噪声对成形的影响, 故采用对称零面积梯形成形可有效抑制由于快通道成形时间缩短带来的噪声增加, 且其抑制低频噪声效果更加优异, 可减小低频噪声波动带来的误触发 ...

2014

0.0

... 探测器采用KETEK公司的VITUS CUBE型X射线硅漂移探测器, 采用热电致冷技术, 使探头组件工作在零下55 ℃, 降低暗电流噪声, 前置放大器采用KETEK公司VIAMP-KC复位型电荷灵敏放大器^[13] ...

2015

0.0

... 2 高信噪比模拟预处理电路设计在核脉冲信号测量中, 提升模拟电路的信噪比有益于幅度提取、谱线能量分辨率等的测量^[14,15,16] ...

2014

0.0

HUANG

Jian-heng

, DU

Yang

, LEI

Yao-hu

, et al(黄建衡, 杜杨, 雷耀虎, 等). Acta Phys. Sin. (物理学报), 2014, 63(16): 168702.

Quantum noise is an important factor influencing the quality of the images obtained by X-ray phase contrast imaging because it induces a random fluctuation on the intensity. In this paper, a method is reported to analyze the noise characteristics of hard X-ray differential phase contrast imaging, and the relationship between the quantum noise and images is determined by numerical simulation. The results show that the mean square deviations of the refractive and scattering images are inversely proportional to the visibility of moiré fringe. That is to say, the higher visibility of moiré fringe leads to the lower mean square deviations of the refractive and scattering images. Therefore, in the case of ensuring an enough X-ray detection efficiency, the improvement in the visibility of moiré fringe will be beneficial to obtaining high-quality phase contrast images and the effective reduction of X-ray exposure dose.

Key Laboratory of Optoelectronic Devices and Systems of Guangdong Province, Key Laboratory of Optoelectronic Devices and Systems of Ministry of Education, College of Optoelectronic Engineering, Shenzhen University, Shenzhen 518060, China

量子噪声引起光强随机波动是影响X射线相衬图像质量的一个重要因素. 提出了一种针对硬X 射线微分相衬成像噪声特性的分析方法,通过数值模拟获得了量子噪声对成像结果的作用规律. 模拟结果表明,折射像和散射像的噪声均方差与叠栅条纹对比度成反比关系,叠栅条纹对比度越大,统计所得的均方差值越小. 在保证X射线探测效率的前提下,提高叠栅条纹对比度将有利于获得高质量的相衬图像,并为有效减少X射线曝光剂量提供条件.

... 2 高信噪比模拟预处理电路设计在核脉冲信号测量中, 提升模拟电路的信噪比有益于幅度提取、谱线能量分辨率等的测量^[14,15,16] ...

2001

0.0

... 2 高信噪比模拟预处理电路设计在核脉冲信号测量中, 提升模拟电路的信噪比有益于幅度提取、谱线能量分辨率等的测量^[14,15,16] ...

2019

0.0

... 梯形成形算法可以通过传递函数法来实现^[17] ...