相干反斯托克斯拉曼及相干反斯托克斯超拉曼光谱微观极化率张量元的简化方案- C3 v对称性

引用本文

汪源, 张贞, 郭源. 相干反斯托克斯拉曼及相干反斯托克斯超拉曼光谱微观极化率张量元的简化方案- C₃ _v对称性 [J]. 光谱学与光谱分析, 2020,40(5): 1382-1387.
WANG Yuan, ZHANG Zhen, GUO Yuan. A Simplified Method of Microscopic Hyperpolarizability of Coherent Anti-Stokes Raman Spectroscopy and Coherent Anti-Stokes Hyper-Raman Spectroscopy- C₃ _v Symmetry [J]. Spectroscopy and Spectral Analysis, 2020,40(5): 1382-1387.
Doi:10.3964/j.issn.1000-0593(2020)05-1382-06 复制到剪切板

Permissions

《光谱学与光谱分析》期刊社所有

相干反斯托克斯拉曼及相干反斯托克斯超拉曼光谱微观极化率张量元的简化方案- C₃ _v对称性

汪源¹, 张贞^2,^*, 郭源^2,³

1. 三亚学院理工学院, 海南三亚 572022

2. 北京分子科学国家研究中心, 中国科学院化学研究所, 北京 100010

3. 中国科学院大学, 北京 100049

*通讯联系人 e-mail: zhangz@iccas.ac.cn

作者简介: 汪源, 1984年生, 三亚学院理工学院副教授 e-mail: wangyuan0155@163.com

收稿日期: 2018-12-05

基金: 国家自然科学基金项目(21503235,21673251,21773258), 海南省自然科学基金项目(119MS074),三亚市院地科技合作项目(2018YD08)资助

摘要

相干反斯托克斯拉曼光谱(CARS)和四阶相干反斯托克斯超拉曼光谱(CAHRS)已经广泛应用于分子的光谱特性、肿瘤细胞的结构及分子反应动力学等问题的研究。对这种复杂的高阶非线性光谱进行定量分析所面临的主要难题是高阶非线性光学过程中分子微观极化率张量元数量众多, 关系复杂。在前期报道的 C_∞ _v对称性分子基团的CARS和CAHRS的微观极化率张量元简化方案的基础上, 对分子对称性更加复杂的 C₃ _v对称性的分子基团的CARS和CAHRS的微观极化率张量元进行简化, 为定量分析 C₃ _v对称性分子基团的CARS和CAHRS光谱信息提供必要的理论基础。首先将CARS微观极化率张量元 β_i'j'k'l'表示为拉曼微观极化率张量元微分 α'_i'j'的乘积, CAHRS微观极化率张量元 β_i'j'k'l'm'表示为超拉曼微观极化率张量元微分 β'_i'j'k'和拉曼微观极化率张量元微分 α'_i'j'的乘积。用 α'_i'j'和 β'_i'j'k'之间的比值关系简化 β_i'j'k'l'和 β_i'j'k'l'm'之间比值。对于 C₃ _v对称类型分子基团的对称振动模式A₁, 9个非零且3个独立的CARS微观极化率张量元可以用 α'_i'j'之间的1个比值参数RSSR进行描述, 21个非零且6个独立的CAHRS微观极化率张量元可以用 α'_i'j'之间及 β'_i'j'k'之间的3个比值参数RSSR,RSS,1HR和RSS,2HR进行描述。然后利用键极化加和模型方法, 通过计算 C₃ _v对称性分子基团中的各个单键与单键之间的耦合关系, 得到 C₃ _v对称性分子基团的对称伸缩振动模式A₁所对应的所有超拉曼微观极化率张量元微分 β'_i'j'k'分量的比值, 结合文献中给出的拉曼微观极化率张量元微分 α'_i'j'分量的比值, 进一步简化 C₃ _v对称性分子基团CARS和CAHRS微观极化率张量元之间的关系。从这些简化了的CARS和CAHRS微观极化率张量元之间的关系, 可以进一步简化CARS和CAHRS信号及广义取向泛函 R_IJK( θ)的表达式, 得到 R_IJK( θ)随界面分子基团取向角度 θ的变化规律。此外, 也详细推导了 C₃ _v对称性分子基团对射式实验构型CAHRS过程的强度因子 d_IJK、广义取向泛函 R_IJK( θ)及广义取向参数 c₂和 c₄的表达式, 为定量分析界面分子取向信息奠定了理论基础。

关键词: 相干反斯托克斯拉曼光谱; 相干反斯托克斯超拉曼光谱; 微观极化率张量元; 键极化加和模型; 分子取向; 定量分析; C₃ _v对称性

中图分类号:O657.37 文献标志码:A

A Simplified Method of Microscopic Hyperpolarizability of Coherent Anti-Stokes Raman Spectroscopy and Coherent Anti-Stokes Hyper-Raman Spectroscopy- C₃ _v Symmetry

WANG Yuan¹, ZHANG Zhen^2,^*, GUO Yuan^2,³

1. Institute of Technology, University of Sanya, Sanya 572022, China

2. Beijing National Laboratory for Molecular Sciences (BNLMS), Institute of Chemistry, Chinese Academy of Sciences, Beijing 100010, China

3. University of Chinese Academy of Sciences, Beijing 100049, China

*Corresponding author

Abstract

Coherent Anti-Stokes Raman Spectroscopy (CARS) and Coherent Anti-Stokes Hyper-Raman Spectroscopy (CAHRS) recently have been widely used in the study of the spectral properties of molecules, the structure of tumor cells and the dynamics of molecular reactions. However, the main difficulty in quantitative analysis CARS and CAHRS is that the number of molecular, microscopic hyperpolarizability tensors in the high order nonlinear optical process are large and the relationships are complex. Our previous work has reported the simplification schemefor CARS and CAHRS microscopic hyperpolarizability tensor elementsbased on the C_∞ _v molecular symmetry. In this paper, we present the simplified scheme for microscopic hyperpolarizability tensor elements of CARS and CAHRS belonging to the C₃ _v symmetry. First, the tensor elements β_i'j'k'l' of the CARS microscopic hyperpolarizability are expressed as the product of the differentiation of Raman microscopic polarizability tensor α'_i'j'. The CAHRS microscopic hyperpolarizability tensor elements β_i'j'k'l'm' are expressed as the product of the differentiation of Raman microscopic polarizability tensor α'_i'j' and the differentiation of hyper Raman microscopic polarizability tensor β'_i'j'k'. The ratio between β_i'j'k'l' and β_i'j'k'l'm' can be simplified by using the ratio between α'_i'j' and β'_i'j'k'. For the symmetric vibrational mode A1 of C₃ _v symmetric type molecular groups, 9 non-zero and 3 independent CARS microscopic hyperpolarizability tensors can be described by a ratio betweenRSSR and α'_i'j', and 21 non-zero and 6 independent CAHRS microscopic hyperpolarizability tensors can be described by three ratios ofRSSR,RSS,1HR andRSS,2HR between α'_i'j' and β'_i'j'k'. Then, the Bond Additivity Model method is used to calculate the coupling between every single bond in the C₃ _v symmetric molecular group, from which the ratio of hyper Raman microscopic polarizability tensor differential β'_i'j'k' for the symmetric vibrational mode A1 of C₃ _v symmetric type molecular groups is obtained. Combined with the ratio of the Raman microscopic polarizability tensor differential α'_i'j' component given in the literature, the relationship between the CARS and CAHRS microscopic hyperpolarizability tensors of C₃ _v symmetry molecular group is further simplified. These relationships between the microscopic hyperpolarizability tensor elements of CARS and CAHRS obtained in this paper are ready to be used for simplifying the expression of CARS and CAHRS signals and generalized oriented functional R_IJK( θ), whichcan obtain the variation of R_IJK( θ) with the orientation angle θ of the interface molecule group. Furthermore, the expressions of intensity factor d_IJK, generalized oriented functional R_IJK( θ) and generalized orientation parameters c₂ and c₄ are obtained. This work provides a theoretical basis for quantitative analysis of interface molecular orientation information.

Keyword: Coherent anti-stokes Raman spectroscopy; Coherent anti-stokes hyper-Raman spectroscopy; Microscopic hyperpolarizability; Bond additivity model; Molecular orientation; Quantitative analysis; C₃ _v symmetry

文章图片

引言

近年来, 三阶非线性光谱技术— — 相干反斯托克斯拉曼光谱(coherent anti-stokes Raman spectroscopy, CARS)^{[1, 2, 3]}及其成像技术^{[4, 5, 6, 7, 8]}以及四阶非线性光谱技术— — 相干反斯托克斯超拉曼光谱(coherent anti-stokes hyper-Raman spectroscopy, CAHRS)^{[9, 10]}已经广泛用于研究分子的光谱特性、肿瘤细胞的结构及分子反应动力学。作为四阶非线性光学过程, CAHRS具有与生俱来的界面选择性, 因此可以用来对界面和生物膜上分子进行研究。尽管三阶的CARS不具有界面选择性^[11], 但用其开展细胞膜分子结构的研究仍然具有其独特的优势^{[4, 5, 6, 7, 8]}。

虽然在界面科学研究领域, 红外光谱(IR)及和频振动光谱(SFG-VS)是目前广为使用的技术手段, 但CARS和CAHRS在实验中不需要红外波段的激光脉冲这一特点可以很好地解决IR及SFG所需要的红外光在穿过含水的凝聚相时有较大的吸收而导致信号损失的难题。这对于界面问题的研究具有更加重要的意义。

在高阶非线性光学过程中, 由于微观极化率张量元数量随非线性光学过程阶数的增加呈指数倍的增加, 因此对于CARS和CAHRS实验信号进行定量分析的关键问题就是如何对非零的三、四阶微观极化率张量元进行化简。我们在前期的工作^[12]中报道了C_∞_v对称性分子基团的CARS和CAHRS的微观极化率张量元进行简化的方案。对于其他对称性分子基团非零张量元的化简结果, 可以用类似的方法得出。与C_∞_v对称的分子基团相比, C₃_v对称的分子基团的非零张量元之间的关系更加复杂。 C_∞_v对称的分子基团CAHRS的243个微观极化率张量元 $β_{i' j' k' l' m'}^{(4)}$ 中非零张量元有6个独立项, 而C₃_v对称性的分子基团有17个独立项^[12]。所以, 有必要探索新的方案对其进行简化。本文给出C₃_v对称性分子基团的CARS和CAHRS的微观极化率张量元简化方案。

1 CARS和CAHRS微观极化率张量元的关系简化

对CARS和CAHRS进行定量分析的前提是得到分子基团不同的微观极化率张量元之间的相对值, 我们前期的工作^[12]对电偶极近似下共振增强时CARS和CAHRS的微观极化率张量元 $β_{i' j' k' l'}^{(3)}$ 和 $β_{i' j' k' l' m'}^{(4)}$ 进行了详细的分析, 得到式(1)和式(2)

$β_{i'j'k'l'}^{(3)} \propto (α'_{i'j'}^{s})^{*} α'_{k'l'}^{s}$ (1)

$β_{i'j'k'l'm'}^{(4)} \propto (β'_{i'j'k'}^{s})^{*} α'_{l'm'}^{s}$ (2)

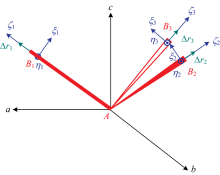
以上两式角标的物理意义, 在文献[12]中已经给出, 这里不在赘述。满足C₃_v对称性分子基团AB₃的分子坐标系如图1所示, (a, b, c)表示分子坐标系, (ξ _i, η _i, ζ _i)表示分子键AB_i的键坐标系(i=1, 2, 3), Δ r_i代表分子键AB_i在键长方向(ζ _i轴)上的振动矢量。从图1可知, 分子基团AB₃有两种伸缩振动模式: 对称伸缩振动模式A₁和反对称伸缩振动模式E。

	Figure Option View Download New Window
	图1 C₃_v对称性分子基团的分子坐标系Fig.1 Molecular coordinate system of C₃_v symmetric molecular group

对于对称伸缩振动模式A₁, 不为零的拉曼微观极化率张量元微分α '_i'j'和超拉曼微观极化率张量元微分β '_i'j'k'的关系可推导如式(3)和式(4)

Raman

$α'_{aa}^{SS} = α'_{bb}^{SS} (= R_{SS}^{R} α'_{cc}^{SS}), α'_{cc}^{SS}$ (3)

Hyper-Raman

$\begin{array}{l} β'_{aac}^{SS} = β'_{aca}^{SS} = β'_{bbc}^{SS} = β'_{bcb}^{SS} (= R_{SS, 2}^{HR} β'_{ccc}^{SS}), β'_{ccc}^{SS} \\ β'_{aaa}^{SS} = - β'_{abb}^{SS} = - β'_{bab}^{SS} = - β'_{bba}^{SS} (= R_{SS, 3}^{HR} β'_{ccc}^{SS}), \\ β'_{caa}^{SS} = β'_{cbb}^{SS} (= R_{SS, 1}^{HR} β'_{ccc}^{SS}) \end{array}$ (4)

其中 $R_{SS}^{R}$ 为拉曼微观极化率张量元微分α '_i'j'之间的比值, $R_{SS, 1}^{HR}$ , $R_{SS, 2}^{HR}$ 和 $R_{SS, 3}^{HR}$ 为超拉曼微观极化率张量元微分β '_i'j'k'之间的比值, 它们都为实数。

利用关系式(1)— 式(4), 可得C₃_v对称类型分子基团对称振动模式A₁的CARS微观极化率张量元 $β_{i' j' k' l'}^{(3)}$ 之间及CAHRS微观极化率张量元 $β_{i' j' k' l' m'}^{(4)}$ 之间的关系。比如CARS微观极化率张量元 $β_{aacc}^{SS}$ 和CAHRS微观极化率张量元 $β_{aaccc}^{SS}$ 可表示为

$β_{aacc}^{SS} \propto (α'_{aa})^{*} α'_{cc} = R_{SS}^{R} (α'_{cc})^{*} α'_{cc} \propto R_{SS}^{R} β_{cccc}^{SS}$ (5)

$β_{aaccc}^{SS} \propto (β'_{aac})^{*} α'_{cc} = R_{SS, 2}^{HR} (β'_{ccc})^{*} α'_{cc} \propto R_{SS, 2}^{HR} β_{ccccc}^{SS}$ (6)

同理, 可以得出所有非零的 $β_{i' j' k' l'}^{(3)}$ 之间及 $β_{i' j' k' l' m'}^{(4)}$ 之间的关系。由此可知, 对于C₃_v对称类型分子基团的对称振动模式A₁, 9个非零且3个独立的CARS微观极化率张量元可以用1个比值参数 $R_{SS}^{R}$ 进行描述, 21个非零且6个独立的CAHRS微观极化率张量元可以用3个比值参数 $R_{SS}^{R}$ , $R_{SS, 1}^{HR}$ 和 $R_{SS, 2}^{HR}$ 进行描述, 使得对非零且独立的CARS及CAHRS微观极化率张量元得到进一步的简化。上述分析同样适用于C₃_v对称类型分子基团的反对称振动模式E以及其他对称类型的分子基团。

表1给出了简化前后C₃_v对称类型分子基团对称伸缩振动模式A₁和反对称伸缩振动模式E的非零独立张量元数目的对比, 从中可以看出, 简化后的CARS及CAHRS微观极化率张量元之间相对关系较之前有进一步的简化。

表1 简化前后C₃_v对称类型分子基团微观极化率张量元非零独立项对比 Table 1 Comparison of relative relations between micropolarizability tensor elements of C₃_v symmetrical type molecular groups before and after simplification

微观极化率张量元		对称伸缩振动模式A₁	反对称伸缩振动模式E
$β_{i' j' k' l'}^{(3)}$	简化前非零独立项简化后非零独立项	3 1	2 1
$β_{i' j' k' l' m'}^{(4)}$	简化前非零独立项简化后非零独立项	6 3	6 6

通过上述方案, 可以将求解C₃_v对称性分子基团的对称伸缩振动模式的CARS和CAHRS微观极化率张量元之间比值的问题转化为求解相同对称性分子基团的相同振动模式下拉曼和超拉曼微观极化率张量元微分之间比值的问题。因为拉曼光谱和超拉曼光谱的微观极化率张量元更容易通过实验测量数据得到, 这样就降低了求解CARS和CAHRS微观极化率张量元之间比值的难度, 有利于对CARS和CAHRS的定量分析。下面我们用键极化加和模型(bond additivity model, BAM)求解分子基团的超拉曼微观极化率张量元微分β '_i'j'k'之间的比值。

2 超拉曼微观极化率张量元微分比值的求解

BAM方法是目前最广泛使用的定量分析和频振动光谱的方法。通过BAM方法能得到各种对称类型分子的拉曼微观极化率张量元微分α '_i'j'之间的比值。该方法能对分子基团进行对称性分析, 把分子基团中每个单键(C_∞_v对称类型)的伸缩振动所对应的拉曼微观极化率张量元微分α '_i'j'耦合起来, 得到对应分子基团各简正振动模式的拉曼微观极化率张量元微分α '_i'j'之间的比值^[13]。在前期的工作^[12]中我们已讨论了C_∞_v对称类型分子基团的拉曼和超拉曼微观极化率张量元微分之间比值的问题。在此基础上, 将通过BAM方法, 得到C₃_v对称性分子基团的超拉曼微观极化率张量元微分β '_i'j'k'之间的比值关系, 从而进一步简化CARS和CAHRS的微观极化率张量元。

C₃_v对称性分子基团AB₃如图1所示, 简正模式的折合质量 $G_{A_{1}}$ 和G_E为^[13]

$G_{A_{1}} = (1 + 2 \cos τ) / M_{A} + 1 / M_{B}$ (7)

$G_{E} = (1 - \cos τ) / M_{A} + 1 / M_{B}$ (8)

其中, τ 为三个单键AB的四面体角, M_A和M_B为原子A和B的质量。简正坐标 $Q_{A_{1}}$ , Q_{E, a}和Q_{E, b}的定义如式(9)— 式(11)^[13]

$Q_{A_{1}} = | Δ r_{1} | + | Δ r_{2} | + | Δ r_{3} |) / \sqrt[]{3 G_{A_{1}}}$ (9)

$Q_{E, a} = (2 | Δ r_{1} | - | Δ r_{2} | - | Δ r_{3} |) / \sqrt[]{6 G_{E}}$ (10)

$Q_{E, b} = (| Δ r_{2} | - | Δ r_{3} |) / \sqrt[]{2 G_{E}}$ (11)

其中|Δ r_i|为单键AB_i(i=1, 2, 3)沿着键坐标系(ξ , η , ζ )中ζ 轴的振动矢量Δ r的模。从表达式(9)— 式(11)可得|Δ r_i|表达式, 其中

$| Δ r_{1} | = \frac{1}{3} (Q_{A_{1}} \sqrt[]{3 G_{A_{1}}} + Q_{E, a} \sqrt[]{6 G_{E}})$ (12)

振动矢量Δ r₁在分子坐标系中的投影分量分别为

$(Δ r_{1})_{a} = | Δ r_{1} | \sin τ, (Δ r_{1})_{b} = 0, (Δ r_{1})_{c} = - | Δ r_{1} | \cos τ$ (13)

其中, |Δ r₂|和|Δ r₃|的表达式及Δ r₂和Δ r₃在分子坐标系中的投影分量可以同理得出。

按照分子基团偶极矩的定义, 键AB_i(i=1, 2, 3)在键坐标系中偶极矩的三个分量可表达如式(14)— 式(16)

$μ_{ξ_{i}} = β_{0} (r_{SS, 2}^{HR} E_{ζ_{i}} E_{ξ_{i}} + r_{SS, 2}^{HR} E_{ξ_{i}} E_{ζ_{i}}) | Δ r_{i} | = 2 β_{0} r_{SS, 2}^{HR} E_{ξ_{i}} E_{ζ_{i}} | Δ r_{i} |$ (14)

$μ_{η_{i}} = β_{0} (r_{SS, 2}^{HR} E_{ζ_{i}} E_{η_{i}} + r_{SS, 2}^{HR} E_{η_{i}} E_{ζ_{i}}) | Δ r_{i} | = 2 β_{0} r_{SS, 2}^{HR} E_{η_{i}} E_{ζ_{i}} | Δ r_{i} |$ (15)

$μ_{ζ_{i}} = β_{0} (r_{SS, 1}^{HR} E_{ξ_{i}} E_{ξ_{i}} + r_{SS, 1}^{HR} E_{η_{i}} E_{η_{i}} + E_{ζ_{i}} E_{ζ_{i}}) | Δ r_{i} |$ (16)

其中β ₀=(∂ β _{ζ ζ ζ}/∂ Δ ζ )₀, $r_{SS, 1}^{HR}$ 和 $r_{SS, 2}^{HR}$ 为单键AB(C_∞_v对称性)的超拉曼微观极化率张量元微分β '_i'j'k'之间的比值^[12], 因为三个单键除了取向以外完全相同, 所以具有相同的β ₀, $r_{SS, 1}^{HR}$ 和 $r_{SS, 2}^{HR}$ ; $E_{ξ_{i}}$ , $E_{η_{i}}$ 和 $E_{ζ_{i}}$ 代表外界光场在各自键坐标系中的投影。将三个键的偶极矩投影到分子坐标系中并加和, 得到

$μ_{a} = μ_{ξ_{1}} \cos τ + μ_{ζ_{1}} \sin τ - \frac{1}{2} μ_{ξ_{2}} \cos τ + \frac{\sqrt[]{3}}{2} μ_{η_{2}} - \frac{1}{2} μ_{ζ_{2}} \sin τ - \frac{1}{2} μ_{ξ_{3}} \cos τ - \frac{\sqrt[]{3}}{2} μ_{η_{3}} - \frac{1}{2} μ_{ζ_{3}} \sin τ$ (17)

$μ_{b} = - μ_{η_{1}} + \frac{\sqrt[]{3}}{2} μ_{ξ_{2}} \cos τ + \frac{1}{2} μ_{η_{2}} + \frac{\sqrt[]{3}}{2} μ_{ζ_{2}} \sin τ - \frac{\sqrt[]{3}}{2} μ_{ξ_{3}} \cos τ + \frac{1}{2} μ_{η_{3}} - \frac{\sqrt[]{3}}{2} μ_{ζ_{3}} \sin τ$ (18)

$μ_{c} = μ_{ξ_{1}} \sin τ - μ_{ζ_{1}} \cos τ + μ_{ξ_{2}} \sin τ - μ_{ζ_{2}} \cos τ + μ_{ξ_{3}} \sin τ - μ_{ζ_{3}} \cos τ$ (19)

将表达式(14)— 式(16)代入式(17)— 式(19)中, 并与分子坐标系中的偶极矩表达式 $μ_{i'} = \sum_{j', k' = a, b, c} β_{i' j' k'} E_{j'} E_{k'} 进行比较即可得 β_{i' j' k'}$ 的表达式, 例如

$β_{ccc} = - β_{0} (| Δ r_{1} | + | Δ r_{2} | + | Δ r_{3} |) \cdot \cos τ (co s^{2} τ + r_{SS, 1}^{HR} si n^{2} τ + 2 r_{SS, 2}^{HR} si n^{2} τ)$ (20)

$β_{aac} = β_{aca} = β_{0} (| Δ r_{1} | - \frac{1}{2} | Δ r_{2} | - \frac{1}{2} | Δ r_{3} |) \cdot r_{SS, 2}^{HR} \cos τ + β_{0} (| Δ r_{1} | + \frac{1}{4} | Δ r_{2} | + \frac{1}{4} | Δ r_{3} |) \cdot \cos τ (r_{SS, 1}^{HR} si n^{2} τ - 2 r_{SS, 2}^{HR} co s^{2} τ - si n^{2} τ)$ (21)

将|Δ r₁|, |Δ r₂|和|Δ r₃|的表达式代入β _i'j'k'的表达式, 并将所得的β _i'j'k'对C₃_v对称性分子基团AB₃对称伸缩振动模式A₁的简正坐标 $Q_{A_{1}}$ 求导, 即可得到属于 $C_{3 v - A_{1}}$ 振动模式不为零的超拉曼微观极化率张量元微分β '_i'j'k'的表达式及其之间的比值 $R_{SS, 1}^{HR}$ , $R_{SS, 2}^{HR}$ 和 $R_{SS, 3}^{HR}$ , 例如

$β'_{aac}^{SS} = β'_{aca}^{SS} = β'_{bbc}^{SS} = β'_{bcb}^{SS} = \frac{1}{2} β_{0} \sqrt[]{3 G_{A_{1}}} \cos τ [(r_{SS, 1}^{HR} - 1) si n^{2} τ - 2 r_{SS, 2}^{HR} co s^{2} τ]$ (22)

$β'_{ccc}^{SS} = - β_{0} \sqrt[]{3 G_{A_{1}}} \cos τ (co s^{2} τ + r_{SS, 1}^{HR} si n^{2} τ + 2 r_{SS, 2}^{HR} si n^{2} τ)$ (23)

$R_{SS, 2}^{HR} = \frac{β'_{aac}^{SS}}{β'_{ccc}^{SS}} = \frac{ta n^{2} τ + r_{SS, 1}^{HR} (ta n^{2} τ + 2) - 2 r_{SS, 2}^{HR} ta n^{2} τ}{2 (1 + r_{SS, 1}^{HR} ta n^{2} τ + 2 r_{SS, 2}^{HR} ta n^{2} τ)}$ (24)

将所得的β _i'j'k'对C₃_v对称性分子基团AB₃反对称伸缩振动模式E的简正坐标Q_E求导, 即可得到属于C₃_v_-_E振动模式不为零的超拉曼微观极化率张量元微分β '_i'j'k'的表达式及其之间的比值。

文献[13]通过BAM方法讨论的C₃_v对称性分子基团AB₃拉曼微观极化率张量元微分α '_i'j'之间的比值进行过详细的讨论, 本文不再烦述。

将表达式(24)代入关系式(6)中, 可得

$β_{aaccc}^{SS} = \frac{ta n^{2} τ + r_{SS, 1}^{HR} (ta n^{2} τ + 2) - 2 r_{SS, 2}^{HR} ta n^{2} τ}{2 (1 + r_{SS, 1}^{HR} ta n^{2} τ + 2 r_{SS, 2}^{HR} ta n^{2} τ)} β_{ccccc}^{SS}$ (25)

通过拉曼和超拉曼实验得到的微观极化率张量元微分之间的比值, 即可确定C₃_v对称性分子基团及其他对称性分子基团的CARS和CAHRS微观极化率张量元之间的相对比值。

3 界面取向角的定量计算

对于C₃_v对称性分子基团CH₃, 根据拉曼及超拉曼实验结果计算可得到的CAHRS微观极化率张量元 $β_{i' j' k' l' m'}^{(4)}$ 之间相对比值, 结合 $β_{i' j' k' l' m'}^{(4)}$ 与CAHRS宏观感应率张量元 $χ_{ijklm}^{(4)}$ 之间及CAHRS宏观有效感应率 $χ_{eff, IJK}^{(4)}$ 和 $χ_{ijklm}^{(4)}$ 之间的关系, 可将C₃_v对称性分子基团AB₃的对称和反对称伸缩振动模式的CAHRS宏观有效感应率 $χ_{eff, IJK}^{(4)}$ 简化成如式(26)的形式

$χ_{eff, IJK}^{(4)} = N_{S} d_{IJK}^{(4)} (< \cos θ > + c_{3}^{(4)} < co s^{3} θ > + c_{5}^{(4)} < co s^{5} θ >) = N_{S} d_{IJK}^{(4)} r_{IJK}^{(4)} (θ)$ (26)

其中 $d_{IJK}^{(4)}$ 为强度因子, 对于对称伸缩振动模式有 $d_{IJK}^{(4)}$ ∝ $β_{ccccc}^{(4), SS}$ , 对于反对称伸缩振动模式有 $d_{IJK}^{(4)}$ ∝ $β_{aaaac}^{(4), AS}$ ; $r_{IJK}^{(4)}$ (θ )为四阶非线性光谱学的取向场泛函; $c_{3}^{(4)}$ 和 $c_{5}^{(4)}$ 为四阶非线性光谱学的广义取向参数, 由微观极化率张量元之间比值、实验构型和偏振组合等信息共同决定。上面分析过程也同样适用于其他对称类型的分子基团。

CAHRS信号的表达式为

$I (ω_{CAHRS}) = A | χ_{eff, IJK}^{(4)} |^{2} I (ω_{1})^{3} I (ω_{2}) = A N_{S}^{2} (d_{IJK}^{(4)})^{2} R_{IJK}^{(4)} (θ) I (ω_{1})^{3} I (ω_{2})$ (27)

$R_{IJK}^{(4)} (θ) = | r_{IJK}^{(4)} (θ) |^{2} = | < \cos θ > + c_{3}^{(4)} < co s^{3} θ > + c_{5}^{(4)} < co s^{5} θ > |^{2}$ (28)

$R_{IJK}^{(4)}$ (θ )直接反映CAHRS信号与分子基团取向之间的关系, 称为广义取向泛函。 $R_{IJK}^{(4)}$ (θ )对分子基团取向角度θ 的依赖关系由 $c_{3}^{(4)}$ 和 $c_{5}^{(4)}$ 决定, 变化规律模拟如图2所示。从图2模拟曲线可以看出, 随着 $c_{3}^{(4)}$ 和 $c_{5}^{(4)}$ 的变化, $R_{IJK}^{(4)}$ (θ )随分子基团取向角θ 变化的规律差别非常明显, 这些差别对于实验的设计与CAHRS信号的分析都具有重要的作用。

	Figure Option View Download New Window
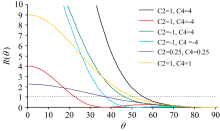	图2 CAHRS过程广义取向泛函随界面分子基团取向角度θ 变化图Fig.2 Variation of generalized orientation functional in CAHRS process with angle of orientation of interfacial molecular groups

利用文献[12]中已知的CAHRS宏观有效感应率 $χ_{eff, SPS}^{(4)}$ 与宏观感应率张量元 $χ_{ijklm}^{(4)}$ 之间的关系, 得到C₃_v对称性分子基团对称振动模式A1的CAHRS宏观有效感应率 ${χ^{(4)}}_{eff, SPS}$ 表达式为

$χ_{eff, SPS}^{(4), SS} = N_{S} d_{SPS}^{(4), SS} r_{SPS}^{(4), SS} (θ) = N_{S} d_{SPS}^{(4), SS} (< \cos θ > + c_{3, SPS}^{(4), SS} < co s^{3} θ > + c_{5, SPS}^{(4), SS} < co s^{5} θ >)$ (29)

其中广义取向泛函 $R_{SPS}^{(4), SS}$ (θ ), 广义取向参数 $c_{3, SPS}^{(4), SS}$ 及 $c_{5, SPS}^{(4), SS}$ , 强度因子 $d_{SPS}^{(4), SS}$ 结果为

$R_{SPS}^{(4), SS} (θ) = | r_{SPS}^{(4), SS} (θ) |^{2} = | < \cos θ > + c_{3, SPS}^{(4), SS} < co s^{3} θ > + c_{5, SPS}^{(4), SS} < co s^{5} θ > |^{2}$ (30)

$c_{3, SPS}^{(4), SS} = \frac{L_{zz}^{2} (ω_{1}) si n^{2} Ω_{1} (1 - 2 R_{SS, 1}^{HR} - 2 R_{SS, 2}^{HR}) - 4 L_{xx}^{2} (ω_{1}) co s^{2} Ω_{1} (1 - 2 R_{SS, 1}^{HR})}{L_{zz}^{2} (ω_{1}) si n^{2} Ω_{1} R_{SS, 2}^{HR} + 2 L_{xx}^{2} (ω_{1}) co s^{2} Ω_{1} (1 - 2 R_{SS, 1}^{HR} + R_{SS, 2}^{HR})}$ (31)

$c_{5, SPS}^{(4), SS} = \frac{(2 L_{xx}^{2} (ω_{1}) co s^{2} Ω_{1} - L_{zz}^{2} (ω_{1}) si n^{2} Ω_{1}) (1 - 2 R_{SS, 1}^{HR} - R_{SS, 2}^{HR})}{L_{zz}^{2} (ω_{1}) si n^{2} Ω_{1} R_{SS, 2}^{HR} + 2 L_{xx}^{2} (ω_{1}) co s^{2} Ω_{1} (1 - 2 R_{SS, 1}^{HR} + R_{SS, 2}^{HR})}$ (32)

$d_{SPS}^{(4), SS} = - \frac{1}{8} β_{ccccc}^{SS} L_{yy} (ω) L_{zz} (ω_{1}) L_{yy} (ω_{2}) \sin Ω_{1} (1 - R_{SS}^{R}) [L_{zz}^{2} (ω_{1}) si n^{2} Ω_{1} R_{SS, 2}^{HR} + 2 L_{xx}^{2} (ω_{1}) co s^{2} Ω_{1} (1 - 2 R_{SS, 1}^{HR} + R_{SS, 2}^{HR})]$ (33)

从上述的表达式可知, 广义取向参数与实验的入射角和出射角密切相关。

基于广义取向泛函 $R_{IJK}^{(4)}$ (θ )及广义取向参数就可通过相同实验构型下两个不同偏振组合的CAHRS信号强度来定量分析界面分子取向的信息。

4 结论

(1)以C₃_v对称性分子基团为例, 利用拉曼微观极化率张量元微分α '_i'j'之间的比值及超拉曼微观极化率张量元微分β '_i'j'k'之间的比值得到CARS微观极化率张量元β _i'j'k'l'和CAHRS的微观极化率张量元β _i'j'k'l'm'之间的比值, 从而简化了CARS和CAHRS微观极化率张量元之间的关系。

(2)利用键极化加和模型方法, 通过计算C₃_v对称性分子基团中的各个单键与单键之间的耦合关系, 求得C₃_v对称性分子基团的对称伸缩振动模式A₁所对应的所有超拉曼微观极化率张量元微分β '_i'j'k'分量的比值, 结合文献[13]中给出的拉曼微观极化率张量元微分α '_i'j'分量的比值, 进一步简化了C₃_v对称性分子基团CARS和CAHRS微观极化率张量元之间的关系。

(3)由简化后非零独立的CAHRS微观极化率张量元之间的关系, 推导出定量分析CAHRS的广义取向泛函以及广义取向参数, 由此得到界面分子的取向信息。

参考文献

文献列表

[1]	Jukka S, Friederike G, Mervi L, et al. Biotechnol. J, 2019, 14: 1800413. [本文引用:1]
[2]	Zirak P, Matz G, Messerschmidt B, et al. APL Photonics. 2018, 3: 092409. [本文引用:1]
[3]	Keigo H, Shuichiro F, Taichi F, et al. APL Photonics, 2018, 3: 092407. [本文引用:1]
[4]	Fu D, Xie X S. Anal. Chem. , 2014, 86: 4115. [本文引用:2]
[5]	Uckermann O, Galli R, Tamosaityte S, et al. PLoS One, 2014, 9: e107115. [本文引用:2]
[6]	Lu F K, Calligaris D, Olubiyi O I, et al. Cancer Res. , 2016, 76(12): 3451. [本文引用:2]
[7]	Cheng J X, Xie X S. Science, 2015, 350: 1054. [本文引用:2]
[8]	Ji M, Lewis S, Camelo-Piragua S, et al. Sci. Transl. Med. , 2015, 7(309): 309ra163. [本文引用:2]
[9]	Fumero G, Batignani G, Dorfman K E, et al. Chem. Phys. Chem. , 2015, 16(16): 3438. [本文引用:1]
[10]	Zhang Z, Bennett K, Chernyak V, et al. J. Phys. Chem. Lett. , 2017, 8(14): 3387. [本文引用:1]
[11]	Fu d, Lu F K, Zhang X, et al. J. Am. Chem. Soc. , 2012, 134(8): 3623. [本文引用:1]
[12]	WANG Yuan, ZHANG Zhen, GUO Yuan(汪源, 张贞, 郭源). Spectroscopy and Spectral Analysis(光谱学与光谱分析), 2019, 39(2): 365. [本文引用:7]
[13]	Wu Hui, Zhang Wenkai, Gan Wei, et al. J. Chem. Phys. , 2006, (125): 133203. [本文引用:5]

2019

0.0