作者简介: 崔双龙, 1988年生, 哈尔滨工业大学仪器科学与工程学院博士研究生 e-mail: cui.shuanglong@qq.com
以红外测温技术为背景, 着重研究了
Based on the infrared temperature measurement technology, this paper focuses on the model
温度是一个重要的物理参数。 温度测量一直是人们研究的热点。 红外测温技术是一种常用的光学测温手段, 具有响应速度快、 不破坏被测目标温度场等优点。 如何将探测器测得的能量更准确的转化为被测目标的真实温度一直是一个重要的研究方向, 存在着许多未解的问题, 黑体辐射在某波段探测器上引起响应的理论计算也是其中之一。
红外测温中, 一直使用f(T)≈ CTn模型来描述黑体波段辐射亮度响应, 该模型中n值的准确性直接影响测温结果的准确性。 对于不同的探测器, 不同的波长区间, 不同的温度范围内, 有不同的C及n[1]。 n值难以准确获取[2], 多数研究者都在使用Inagaki及Okamoto在1996年提出的三个拟合结果[3], 还不能很好的扩展到任意波段的探测器。 本文通过理论推导, 提出了一种可以替代f(T)≈ CTn模型的通用公式, 通用公式与原模型f(T)≈ CTn相比, 最大的优势在于可以在任意波段内, 不需考虑温度分区, 直接计算求取黑体波段辐射亮度响应f(T), 具有通用性。 黑体波段辐射亮度响应的通用公式进一步完善了红外测温技术的基础理论。
红外测温中, 探测器接收到的辐射能量包括三部分: 目标自身发出的辐射, 目标反射环境的辐射和大气辐射。 测得的物体表面光谱辐射亮度为[4]
式(1)中, Lλ 表示光谱辐射亮度, τ aλ 为光谱大气透过率, ε λ 为被测目标的光谱发射率, Ts为被测目标表面温度, ρ λ 为被测目标的反射率, Tu为被测目标周围环境温度, ε aλ 为大气的光谱发射率, Ta为大气温度。 在红外测温技术使用的窄波段范围内, ε λ , τ aλ , ρ λ , ε aλ 可近似认为与λ 无关。 当被测目标为朗伯体时, 公式变化为[4]
式(2)中, Tr为探测器测得物体的辐射温度。 f(T)为某段波长范围内, 黑体辐射亮度在探测器上引起的响应, 本文称其为黑体波段辐射亮度响应。 f(T)可近似为f(T)≈ CTn。
式(3)中, λ 2及λ 1为探测器响应波段的上下限, Rλ 为探测器的光谱响应度, Mbλ (T)为黑体在波长λ 处温度T时的辐射出射度, 由普朗克公式计算。 若被测目标为灰体, 即ε =α =1-ρ , 对大气可认为ε a=α a=1-τ a, 通过将f(T)≈ CTn代入可得[4]
式(4)即为常用的红外测温公式。 根据文献[3], 273~473 K范围内, 有效波长2~5 μ m的InSb探测器f(T)≈ 1.12× 10-13× σ T8.68, 有效波长6~9 μ m的HgCdTe探测器f(T)≈ 5.16× 10-5× σ T5.53, 有效波长8~13 μ m的HgCdTe探测器f(T)≈ 0.136× σ T4.09, 其中σ =5.6679× 10-8[W· (m2· K4)-1]为斯蒂芬玻尔兹曼常数。
文献[1, 2]指出, f(T)≈ CTn对于不同的探测器, 不同的波长区间, 不同的温度范围内, 有不同的C及n。 且难以确定。 针对此现象, 对Planck公式的近似公式“ 维恩近似公式” 进行积分, 通过理论推导给出了一种可以替代f(T)≈ CTn模型的通用公式, 该通用公式可通过探测器的光谱响应范围及温度, 计算黑体波段辐射亮度响应。
根据式(3)对Planck公式进行积分, 未能得到有效的解析解, 因而退一步对“ 维恩近似公式” 进行积分。 对于普朗克公式当
其中c1和c2为普朗克辐射常数, c1=2π hc3=3.741 5× 108 (W· μ m4· m-2), c2=hc/KB=1.438 79× 104 (μ m· K)。 式(5)即为维恩近似公式。 实际应用中, 在误差可接受的情况下, 维恩近似公式可以替代普朗克公式使用。 Rλ 一般可拟合为λ 的二次多项式, 即Rλ =aλ 2+bλ +c, 则黑体波段辐射亮度响应为
设x=c2/λ T则
特别的, 当Rλ =c为常数, 即式(7)中a=b=0时
式(7)即为本工作提出的计算黑体波段辐射亮度响应的通用公式, 可计算任意波段内的f(T), 将f(T)带入式(2)后可通过二分法或迭代法计算被测目标温度Ts。
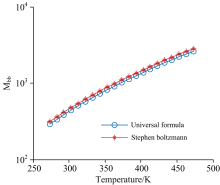
斯蒂芬玻尔兹曼定律是将普朗克公式在全波段积分所得, 表达式为Mbb=σ T4, 其中σ 为斯蒂芬波尔兹曼常数, σ =5.667 9× 10-8[W· (m2· K4)-1]。 黑体波段辐射亮度响应公式按全波段计算, 即x1=0, x2=∞ 得到的结果理论上是与斯蒂芬玻尔兹曼定律近似的, 可用于仿真验证。 全波段积分得
σ '=5.238 5× 10-8[W· (m2· K4)-1]与σ =5.667 9× 10-8[W· (m2· K4)-1]接近, 差值为0.429 4× 10-8[W· (m2· K4)-1], 其偏差来自于维恩公式对普朗克公式的近似。 将斯蒂芬玻尔兹曼定律与式(9)绘图对比如图1。
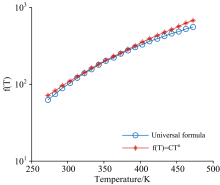
文献[3]给出了三种探测器在273~473 K内f(T)≈ CTn的拟合结果, 取其中有效波长8~13 μ m的HgCdTe探测器进行仿真对比。 文献中探测器响应曲线及拟合结果如图2。
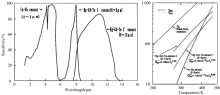 | 图2 文献[3]中探测器响应曲线及拟合结果Fig.2 Detector response curves and fitting results in [3] |
根据式(7)进行求解并将之与文中给出的f(T)≈ 0.136× σ T4.09进行对比, 如图3。 从图中可以看出通用公式计算结果与参考文献拟合结果基本一致。
通过将通用公式与斯蒂芬玻尔兹曼定律及文献[3]中拟合结果的对比, 说明了通用公式的正确性。 通用公式源于维恩近似公式, 适用于
为进一步验证通用公式的有效性, 设计实验进行验证。 实验方法为: 选取测量目标, 调节其表面温度至某一定值且稳定, 通过铂电阻测定其表面温度Ts及环境温度Tu, 分别记录。 使用热像仪对其进行测量, 将热像仪发射率设置为1, 测量目标温度, 记录示值为Tr。 根据Ts, Tu及Tr可计算目标发射率ε (近距离测量, 大气透过率τ 近似为1; 被测目标近似为灰体, 即ρ =1-ε )[1]
调节热像仪的发射率, 使其示值温度T=Ts, 记此时发射率ε 0为目标发射率参考值[6, 7]。 若ε ≈ ε 0, 则通用公式可以用于红外测温技术的工程实践之中。
以实验室内面源辐射体为目标进行实验, 已知该辐射体发射率高于0.9, 按4.1所述实验方法进行实验, 连续测量22组数据, 列于表1。
| 表1 面源辐射体实验数据 Table 1 Surface source radiator experimental data |
根据参考值ε 0的测量数据, 有效数字取小数点后2位。 通过拉伊达准则进行粗大误差判别, 最后将有效数据求取均值,
通过实验, 验证了通用公式的正确性。 实验结果
红外测温技术中, 多数研究者通过模型f(T)≈ CTn来描述黑体波段辐射亮度响应, 式中n值准确性直接影响测温结果的准确性, 且难以准确获取。 提出了一种黑体波段辐射亮度响应的通用公式。 并通过仿真说明了通用公式的正确性。 进一步通过实验证明了, 通用公式可以替代f(T)≈ CTn模型, 应用于工程实践。 通用公式与原模型相比, 最大的优势是可以在任意波段内, 不需考虑温度分区, 通过理论计算的方式求取f(T), 具有通用性。 黑体波段辐射亮度响应的通用公式进一步完善了红外测温技术的基础理论。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|