基于核岭回归方法的恒星大气物理参数的自动测量

引用本文

李航飞, 屠良平, 胡煜寒, 刘昊, 赵健. 基于核岭回归方法的恒星大气物理参数的自动测量[J]. 光谱学与光谱分析, 2020,40(4): 1297-1303.
LI Hang-fei, TU Liang-ping, HU Yu-han, LIU Hao, ZHAO Jian. Automatic Measurement of Stellar Atmospheric Physical Parameters Based on Kernel Ridge Regression Method[J]. Spectroscopy and Spectral Analysis, 2020,40(4): 1297-1303.
Doi:10.3964/j.issn.1000-0593(2020)04-1297-07 复制到剪切板

Permissions

《光谱学与光谱分析》期刊社所有

基于核岭回归方法的恒星大气物理参数的自动测量

李航飞, 屠良平^*, 胡煜寒, 刘昊, 赵健

辽宁科技大学理学院, 辽宁鞍山 114051

*通讯联系人 e-mail: tuliangping@ustl.edu.cn

作者简介: 李航飞, 1991年生, 辽宁科技大学理学院硕士研究生 e-mail: texde3@163.com

收稿日期: 2019-03-17 接受日期: 2019-07-26

基金: 国家自然科学基金项目(U1731128, 61202315), 辽宁科技大学青年拔尖人才项目(601011506)资助

摘要

我国大科学工程项目LAMOST巡天计划每观测夜能获取多达数万条天体光谱数据, 天文学家通过对天体光谱的分析观察可以获取有效的天文信息用于天文学或天体物理学的研究。而针对海量数据, 寻找自动方法分析天体光谱并进行天体各种物理参数的测量就具有重要研究意义和价值。这一课题也吸引了许多学者进行研究, 但目前所尝试的算法和相应结果仍然需要进一步改进, 针对这一需求深入研究了核岭回归(KRR)方法在恒星大气物理参数(包括有效温度、表面重力和金属丰度)自动测量方面的应用, 特别是在我国大科学工程项目LAMOST所释放光谱数据上的应用。核岭回归是岭回归算法的进一步发展, 而岭回归是最小二乘方法的一种变形, 其具有解决高维多重共线性问题的能力。所以KRR方法适合于处理高维的天体光谱信息, 从LAMOST的第五期释放数据中随机选择了2万条被识别为恒星的光谱数据用于实验测试, 该数据既包含低信噪比数据, 也包含高信噪比数据( g, r, i波段平均信噪比最低至6.7, 最高到793)。首先, 本文对光谱进行预处理, 包括三个步骤: (1)利用小波变换对光谱数据进行去噪处理; (2)因为LAMOST采用的是后期修正的流量定标设计, 所以还通过流量归一化来避免部分光谱流量值不准确的问题; (3)由于每条光谱维数高达数千维, 利用主成分分析方法(PCA)对光谱进行了降维。然后, 利用KRR方法建立了光谱数据和标准化后的三大参数值之间的回归模型。最后, 通过设计进行不同的组合实验对KRR算法模型进行了测试分析, 并与经典算法支持向量回归(SVR)进行了对比。综合所有实验结果显示KRR方法对应的有效温度、表面重力和金属丰度的测试平均绝对误差分别为82.989 7 K, 0.185 8 dex和0.121 1 dex, 优于SVR的144.230 8 K, 0.188 6 dex和0.124 6 dex。特别是KRR在温度测试结果上有较大优势, 由此表明KRR方法能够有效地应用于天体光谱特别是恒星光谱参数的自动测量处理中。

关键词: 天体光谱; 恒星大气物理参数; 核岭回归

中图分类号:TP29 文献标志码:A

Automatic Measurement of Stellar Atmospheric Physical Parameters Based on Kernel Ridge Regression Method

LI Hang-fei, TU Liang-ping^*, HU Yu-han, LIU Hao, ZHAO Jian

School of Science, University of Science and Technology Liaoning, Anshan 114051, China

*Corresponding author

Abstract

Through observing and analyzing these celestial spectra, astronomers can obtain effective astronomical information to research the theory of astronomy and astrophysics. And a large scientific engineering project in China, the LAMOST survey program can obtain a large number of celestial spectra every observation night. For the massive data, it is very important to find an automatic method to analyze the celestial spectrum and measure various physical parameters of the celestial body. In fact, many scholars had been attracted to research this topic before, however, the current algorithms and corresponding results that were presented by them cannot meet the accuracy of manual measurement, and it means that we should find more appropriate algorithms to improve the effect of automatic processing. In this paper, we study deeply the applications of the Kernel Ridge Regression (hereinafter referred to as KRR) method in the automatic measurement of the stellar atmosphere physical parameters (including temperature, gravity and chemical abundance), especially the applications in the spectral data released by LAMOST. The KRR is a further development of the Ridge Regression algorithm, and the Ridge Regression is a variant of the Least Squares Method with a regularization term, it has an ability to solve high dimensional multi-collinearity problems. Therefore, the KRR method is suitable for processing high-dimensional celestial spectral information. In this paper, 20 000 stellar spectral data identified as stars are randomly selected from the release data of LAMOST for experimental testing. The data set contain spectra with low SNR and high SNR (the average SNR in g, r, i-band are from 6.7 up to 793). In this paper, we preprocess all the spectra firstly, including three steps: one is the de-noise phase based on the wavelet transform; In order to avoid some inaccuracies in the spectral flux value, the second step is spectral flux normalization; Because the dimension of each spectrum is up to several thousand dimensions, the principal component analysis method (PCA) is used to reduce the spectral dimensions as the third step. Then, we establish a regression model between the spectral data and the normalized three stellar parameters based on the KRR method. Finally, we design many different combinations of experiments to test and analyze the KRR model, and compare its results with the results of the classical algorithm SVR. All the experimental results using KRR method show that the average absolute error of temperature, gravity and chemical abundance is 82.989 7 K, 0.185 8 dex and 0.121 1 dex, respectively, it is better than the result of the SVR which is 144.230 8 K, 0.188 6 dex and 0.124 6 dex, respectively. In particular, the KRR method has a large advantage in temperature test results, which indicates that the KRR method can be effectively applied to the automatic measurement of the stellar spectral parameters.

Keyword: Celestial spectrum; Stellar atmospheric physical parameters; Kernel ridge regression

文章图片

引言

在天文学研究中, 各类天体对应的物理参数对于研究天体的形成、结构以及演化具有极其重要的作用。要想精确的测量天体的某一个物理参数如质量、大小及年龄, 科学家往往要基于几十个精细物理系统来观测分析得到。但在面对大型巡天计划如我国大科学工程LAMOST项目^[1]时, 这种方式就不适用了, 在大样本统计天文学中, 科学家也可以容忍精度稍低但计算效率更高的方法。 LAMOST这类项目可以获取数百万甚至上千万的天体光谱, 这些数据为我国天文学家研究银河系和星系的形成与演化, 提供了有力的基础性数据, 也为许多天文学研究取得重大突破奠定了基础^[2]。而利用光谱数据研究快速高效的算法来测量天体目标的物理参数显然具有重要意义和价值。

基于LAMOST光谱数据, 本文主要研究其中一类天体— — 恒星大气物理参数的自动测量。恒星大气物理参数主要包含有效温度(Teff), 金属丰度([Fe/H]), 表面重力(Log g)。这一课题吸引了一些学者进行了相关算法方面的研究, 如王杰^[3]等提出了线指数方法, 即通过选择最佳的线指数来建立回归模型, 进而进行回归预测。潘儒扬^[4]等提出的深度学习方法, 也被应用在恒星大气物理参数测量方面, 他指出深度学习在处理非线性数据的时候表现出比较好的特性。 Yang^[5]等采用反馈型神经网络算法进行参数测量, 通过采用自编码进行特征提取, 之后建立模型进行参数测量。 Lu^[6]等采用LASSO方法进行天体光谱参数测量, 即通过小波变化进行降噪, 采用支持向量回归(support vector regression, SVR)方法进行特征提取, 测量结果在接受范围内。 Liu^[7]等采用SVR模型进行天体表面重力的参数测量, 实验结果表明该方法在巨行星的表面重力的参数测量准确度方面有提升, Li^[8]等提出一种通过线性模式提取光谱的线性支持特征, 能够定量的评估提取的特征贡献度, 通过合理的选择特征, 利用线性回归方法进行参数测量, 预测结果的平均绝对误差在接受范围内。而利用核思想的则有Xiang等^[9]提出的基于核主成分思想的恒星参数测量方法, 该方法在LAMOST信噪比大于50以上的恒星光谱数据中测量效果非常好。本文采用的是核岭回归(kernel ridge regression, KRR)^[10]算法, 首次将该算法应用在天体光谱参数测量上面, 实验结果表明该方法在天体光谱参数测量方面是可行的。

1 方法介绍

大多数变量之间都存在着这样或者那样的关系, 而这些不确定的关系导致模型训练的时候参数趋向无穷大, 影响模型的质量, 其中影响比较大的就是多重共线性。多重共线性是变量之间存在高度相关性, 导致参数无法求出确定解。在大数据时代, 数据一般都是高维, 所以共线性^[11]问题不容忽视, 而KRR方法在解决这一问题时具有优势。

本文要处理的光谱每条采样点有几千个, 即相对应的数据高达数千维, 所以在处理时通常要进行降维。降维后的低维特征在常规方法上显示区分度不高, 所以本文引入了具有核方法思想的KRR方法, 该方法是先利用核函数将数据映射到高维空间, 数据在高维空间数据间的特征会更容易区分, 然后应用岭回归方法, 对映射后的数据进行回归处理。岭回归方法实际是最小二乘法(LSM)的变形, 它是在LSM的基础上添加了一个正则化项, 而KRR方法则是核函数和岭回归方法的结合体。 KRR方法在小样本数据上有较高的准确性, 所以该方法从原理上来说适合在天体光谱参数测量方面的应用。

1.1 基础模型解释

对于线性回归模型

$\dot{y} = Xw + ε$ (1)

式(1)中X是数据矩阵, w是权值系数, ε 是误差, $\dot{y}$ 为预测值。

误差方程为

$\min \frac{1}{n} \overset{n}{\sum_{i = 1}} {(y - \dot{y})}^{2} = \frac{1}{n} \overset{n}{\sum_{i = 1}} {(y - Xw + ε)}^{2}$ (2)

式(2)中y是真实值。

对误差方程中w求积分得

$w = (X^{T} {X)}^{- 1} X^{T} y$ (3)

式(3)中如果X^TX逆矩阵不存在, 这对参数的估计十分不利, 无法求出一个准确的w值, 最终的预测模型将无法建立。因此为了解决这个问题, 添加一个正常数的矩阵, 只要保证λ 的数值不为零, 此时(X^TX+λ I)就不为零, 从而有效解决了共线性的问题。当岭回归参数λ =0, 就是LSM, 当岭回归参数λ 趋向无穷大的时候, 岭回归系数趋向于0。

岭回归是有偏回归, 它的结果虽然使得残差平方和变大, 但是会使系数检验变好, 这样可以算出合理的系数。岭回归虽然放弃了LSM的无偏性, 损失了精度, 但得到的回归系数却能够更加符合实际情况^[12]。在数据分析和建模中, 当预测变量高度相关时, 岭回归产生的系数比LSM预测的系数具有更好的稳定性^[13]。

岭回归本质上是在LSM的基础上添加了一个二范数的正则化, 岭回归的目标函数如式(4)

$\min_{w} ‖ Xw - y ‖_{2}^{2} + λ ‖ w ‖_{2}^{2}$ (4)

由于数据的多样性, 单纯的线性回归可能不能更好的解决问题, 因此, 可以把数据通过核函数映射到一个高维空间, 使得这些数据在这个高维空间更容易划分, 具体的操作就是选取一个核函数, 令x→ F(x), 原理和岭回归基本是一样的, 目标函数如式(5)

$\min_{w} \sum ε^{2} + λ ‖ w ‖_{2}^{2}$ (5)

函数需要满足的条件

$s.t. ε = y - wΦ (x_{i})$ (6)

引入Lagrange系数可得

$L (w, Φ (x), α) = λ ‖ w ‖^{2} + \sum ε^{2} + α (y - wΦ (x_{i}) - ε)$ (7)

对式(7)进行微分可得

$\begin{array}{l} w = \frac{1}{2 λ} \overset{n}{\sum_{i = 1}} αΦ (x_{i}) \\ α = 2 ε \end{array}$ (8)

整理后得

$y = (K + λI) α$ (9)

最后的预测公式为

$\dot{y} = \overset{n}{\sum_{i = 1}} α_{i} Φ (x_{i}, \dot{x}) = y' {(K + λI)}^{- 1} k$ (10)

式中 $K = Φ (x_{i}, x_{j}), k = \sum k (x_{i}, \dot{x}) 。$

1.2 评价指标

本文采用均方误差(mean squared error, MSE)和平均绝对误差(mean absolute error, MAE)来作为光谱参数测量结果的评价标准, 计算方式见式(11)和式(12)

$MSE = \frac{1}{n} \overset{n}{\sum_{i = 1}} (y_{i} - {\dot{y}}_{i})^{2}$ (11)

$MAE = \frac{1}{n} \overset{n}{\sum_{i = 1}} |y_{i} - {\dot{y}}_{i}|$ (12)

其中 ${\dot{y}}_{i}$ 表示第i个预测值, y_i表示对应的真实值, n为样本总量。

2 实验部分

2.1 模型评价标准

模型训练好之后, 对输入的数据会有对应的输出, 该输出值就为预测值, 一般预测值越接近真实值越好, 误差是指预测值和真实值的差, 模型的好坏在于预测新样本的时候有较小的误差, 误差越小模型的泛化能力越强。当数据量不足的时候, 模型会出现欠拟合, 反之则会出现过拟合现象。

常用的模型实验方法中, 留出法比较常见, 留出法随机保留一部分数据留作测试, 其他用于模型训练, 一般来说采用2/3或者4/5的样本数据用于训练, 剩余的样本用于测试, 若训练集数据太多, 测试集数据太少评估结果往往不具备足够的可信度, 若测试集过多, 模型可能会欠拟合, 数据集的特征拟合不完整, 因此数据集的选择尤为重要, 实验随机选择保留原始数据的30%作测试数据, 其他数据作训练数据。

2.2 数据

采用LAMOST DR5光谱数据, 从中随机选择了2万条恒星光谱, 其中三个恒星大气物理参数值的范围为: 有效温度(Teff): 3 763.858 362.43 K, 表面重力(Log g): 0.3194.897 dex, 金属丰度([Fe/H]): -2.4770.62 dex, 所有光谱g, r, i波段平均信噪比覆盖范围为6.7793。

2.3 步骤

实验设计步骤如下:

(1)利用小波变换对光谱进行去噪, 并进行流量归一化;

(2)采用主成分分析方法(principal component analysis, PCA)对光谱数据进行降维, 通过实验分析本文选择降维至300维;

(3)利用留出法随机抽取样本中70%为训练数据, 剩余30%为测试数据, 共进行50次组合实验;

(4)应用KRR方法分别对三个参数进行模型训练及测试, 进行误差分析。

(5)采用经典SVR方法在相同数据上进行训练测试, 并与KRR方法的结果进行对比。

2.4 结果

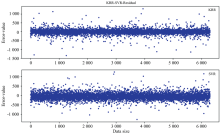
(1)有效温度预测结果对比图

图1和图2中左侧图横轴为天体有效温度的真实值, 纵轴为天体光谱有效温度的预测值, 显然, 数据点越靠近中心线y=x, 预测结果越接近真实值, 右侧图相应为误差统计直方图。直观上可以看出, KRR方法有效温度的预测值比SVR方法有更多的点接近真实值, 从直方图也可看出, 图中误差值接近0的频数要远远大于SVR中误差接近0的频数。 KRR方法在有效温度方面的预测结果要优于SVR方法。

	Figure Option View Download New Window
	图1 KRR方法有效温度估计值和真实值一一对应图及误差对比图Fig.1 KRR method effective temperature estimation value and true value one-to-one correspondence diagram and error comparison diagram

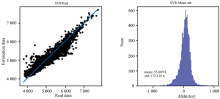	Figure Option View Download New Window
	图2 SVR方法有效温度估计值和真实值一一对应图及误差对比图Fig.2 SVR method effective temperature estimation value and true value one-to-one correspondence diagram and error comparison diagram

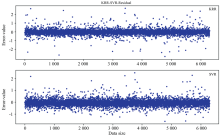
(2)表面重力预测结果对比图

从图3和图4左侧图可以看出, 两种方法预测值和真实值形成的数据点分布类似, KRR方法中出现的异常点略多, SVR方法预测结果相对比较稳定。从右侧图可以看出, KRR方法要比SVR方法略好, 有更多的点接近真实值。总体来说两种方法在表面重力方面的测量结果KRR方法在准确度上要好于SVR方法, 但是在稳定性上稍差。

	Figure Option View Download New Window
	图3 KRR方法表面重力估计值和真实值一一对应图及误差对比图Fig.3 KRR method surface gravity estimation value and true value one-to-one correspondence diagram and error comparison diagram

	Figure Option View Download New Window
	图4 SVR方法表面重力估计值和真实值一一对应图及误差对比图Fig.4 SVR method surface gravity estimation value and true value one-to-one correspondence diagram and error comparison diagram

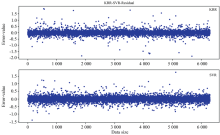
(3)金属丰度预测结果对比图

从图5和图6左侧图可以看出KRR方法个别预测值偏差比较大, 部分数据点分布比较零散, SVR方法相对来说比较稳定。右侧可以看出KRR方法优势更明显, 符合理想要求的数据点比较多, 误差值接近0的频数比较大。整体来说, SVR方法比较稳定, KRR方法在精确度方面较好, 但是预测不稳定, 预测结果较容易出现大误差。

	Figure Option View Download New Window
	图5 KRR方法金属丰度估计值和真实值一一对应图及误差对比图Fig.5 KRR method metal abundance estimation value and true value one-to-one correspondence diagram and error comparison diagram

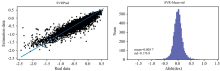	Figure Option View Download New Window
	图6 SVR方法金属丰度估计值和真实值一一对应图及误差对比图Fig.6 SVR method metal abundance estimation value and true value one-to-one correspondence diagram and error comparison diagram

	Figure Option View Download New Window
	图7 有效温度残差对比图Fig.7 Effective temperature residual contrast diagram

	Figure Option View Download New Window
	图8 表面重力残差对比图Fig.8 Surface gravity residual contrast diagram

(4)残差对比图

正常情况下残差图上的点随机分布在以0为横轴的直线上下, 表明预测值的随机性和不确定性, 随机性和不可预测性是任何回归模型的关键组成部分。越多的残差数据点越接近0轴表示相对误差越小, 回归方法预测结果越准确。从三个参数对应KRR和SVR两种方法的残差对比图(2.7, 2.8, 2.9)可以看出, 在有效温度测量上, KRR方法数据点分布带要比SVR数据点分布带窄, 说明KRR在有效温度测量上有较明显优势, 而另外两个参数并没有明显区别。不过从残差图中可以看到, KRR方法预测结果中残差较大的异常点相比SVR稍多, 且在三个参数残差图中异常点有效温度的误差范围大多聚集在500K左右, 表面重力的在3 dex左右, 金属丰度的在1.5 dex左右, 结合表1和表2的误差统计, 这反过来说明KRR方法在非异常点处更加精确。

	Figure Option View Download New Window
	图9 金属丰度残差对比图Fig.9 Metal abundance residual contrast diagram

表1 KRR预测结果误差统计表 Table 1 KRR Statistical table of errors in prediction results of parameters

表2 SVR预测结果误差统计表 Table 2 SVR Statistical table of errors in prediction results of parameters

(5)误差结果统计分析表

表1是本文KRR方法50次组合实验总的误差统计表, 从表中可以看到KRR方法有效温度的预测误差的平均绝对误差值为82.989 7, 其结果要比SVR方法的144.230 8好很多, 表面重力和金属丰度两个结果KRR稍微优于SVR方法。本文实验数据中有效温度的数值覆盖范围是3 763.858 362.43 K数值比较大, 而另外两个参数数值较小, 说明KRR方法在大数值方面有较好的预测结果, 在小数值上面预测结果和SVR相差无几。但是在均方误差方面, 由于KRR方法预测结果中存在较大的偏差, 导致均方误差要大于SVR方法。总体来说KRR方法更适合有效温度的预测。

3 结论

将KRR方法应用于恒星大气物理参数测量, 该方法能在天体光谱参数测量方面取得比较理想的预测结果, 对高纬度小样本有较好的鲁棒性。为了避免偶然数据的影响, 本文将SVR方法和该方法作对比, 实验结果发现KRR方法在有效温度的测量方面具有较高的预测精度, 表面重力和金属丰度优势较小, 但总体的预测结果是可以接受, 因此该方法在天体光谱参数测量方面是可行的。由于KRR方法添加了正则项, 权值系数矩阵是不稀疏的, 随着数据量的增加, 模型训练时间越来越长, 下一步将针对训练时间进行优化。

参考文献

文献列表

[1]	SHI Jian-rong(施建荣). Chinese Science Bulletin(科学通报), 2016, (12): 1330. [本文引用:1]
[2]	ZHAO Yong-heng(赵永恒). Physics(物理), 2015, 44(4): 205. [本文引用:1]
[3]	WANG Jie, PAN Jing-chang, TAN Xin(王杰, 潘景昌, 谭鑫). Spectroscopy and Spectral Analysis(光谱学与光谱分析), 2014, 34(3): 833. [本文引用:1]
[4]	PAN Ru-yang, LI Xiang-ru(潘儒扬, 李乡儒). Acta Astronomica Sinica(天文学报), 2016, 57(4): 379. [本文引用:1]
[5]	Yang T, Li X. Monthly Notices of the Royal Astronomical Society, 2015, 452(1): 158. [本文引用:1]
[6]	Lu Y, Li X. Monthly Notices of the Royal Astronomical Society, 2015, 452(2): 1394. [本文引用:1]
[7]	Liu C, Fang M, Wu Y, et al. The Astrophysical Journal, 2015, 807(1): 4. [本文引用:1]
[8]	Li X, Lu Y, Comte G, et al. The Astrophysical Journal Supplement Series, 2015, 218(1): 3. [本文引用:1]
[9]	Xiang M S, Liu X W, Shi J R, et al. Monthly Notices of the Royal Astronomical Society, 2017, 464(3): 3657. [本文引用:1]
[10]	Welling M. Max Welling’s Classnotes in Machine Learning, 2013. 1. [本文引用:1]
[11]	LIN Jin-feng(林津峰). Fujian Computer(福建电脑), 2018, 34(8): 118. [本文引用:1]
[12]	LUO Wen-hai, ZHANG Qing-feng(罗文海, 张庆凤). Health Vocational Education(卫生职业教育), 2018, 36(16): 157. [本文引用:1]
[13]	WANG Rui(王锐). Economic Research Guide(经济研究导刊), 2018, (22): 144. [本文引用:1]

2016

0.0

... 但在面对大型巡天计划如我国大科学工程LAMOST项目^[1]时, 这种方式就不适用了, 在大样本统计天文学中, 科学家也可以容忍精度稍低但计算效率更高的方法 ...

2015

0.0

... LAMOST这类项目可以获取数百万甚至上千万的天体光谱, 这些数据为我国天文学家研究银河系和星系的形成与演化, 提供了有力的基础性数据, 也为许多天文学研究取得重大突破奠定了基础^[2] ...

2014

0.0

WANG

Jie

, PAN

Jing-chang

, TAN

Xin

(王杰, 潘景昌, 谭鑫). Spectroscopy and Spectral Analysis(光谱学与光谱分析), 2014, 34(3): 833.

In the present paper, the kernel partial least squares regression (KPLSR) method was used to measure the atmospheric physical parameters (effective temperature, surface gravity, an d chemical abundance) based on the use of Lick line index. The proposed method can reduce the computation cost and achieve an ideal measure precision. At first, the Lick indices of Kurucz synthetic spectra were extracted and the kernel regression model between the Lick indices and the atmospheric physical parameters was established using the KPLSR method. Then the physical parameters of DR8 measured spectral data were computed by the kernel regression model for testing. The test results were compared with the atmospheric physical parameters provided by SEGUE SSPP and were good results. In addition, we added a signal-to-noise ratio (SNR) of 10, 20, 30, 40, 50, 70, 90 and 120 Gaussian white noise to the Kurucz spectra. And the resulting spectra of different SNR were used to test the impact of noise on the parameter measurement. The experimental results show that the kernel regression model is sensitive to noise, the higher the SNR of spectral data, the higher the prediction accuracy of the physical parameters. The method of KPLSR based on Lick line index has small amount of computation and fast training speed, which is suitable for measuring physical parameters of stellar atmosphere.

[Wang Jie; Pan Jing-chang; Tan Xin] Shandong Univ, Sch Mech Elect & Informat Engn, Weihai 264209, Peoples R China.

... 这一课题吸引了一些学者进行了相关算法方面的研究, 如王杰^[3]等提出了线指数方法, 即通过选择最佳的线指数来建立回归模型, 进而进行回归预测 ...

2016

0.0

... 潘儒扬^[4]等提出的深度学习方法, 也被应用在恒星大气物理参数测量方面, 他指出深度学习在处理非线性数据的时候表现出比较好的特性 ...

2015

0.0

... Yang^[5]等采用反馈型神经网络算法进行参数测量, 通过采用自编码进行特征提取, 之后建立模型进行参数测量 ...

2015

0.0

... Lu^[6]等采用LASSO方法进行天体光谱参数测量, 即通过小波变化进行降噪, 采用支持向量回归(support vector regression, SVR)方法进行特征提取, 测量结果在接受范围内 ...

2015

0.0

... Liu^[7]等采用SVR模型进行天体表面重力的参数测量, 实验结果表明该方法在巨行星的表面重力的参数测量准确度方面有提升, Li^[8]等提出一种通过线性模式提取光谱的线性支持特征, 能够定量的评估提取的特征贡献度, 通过合理的选择特征, 利用线性回归方法进行参数测量, 预测结果的平均绝对误差在接受范围内 ...

2015

0.0

2017

0.0

... 而利用核思想的则有Xiang等^[9]提出的基于核主成分思想的恒星参数测量方法, 该方法在LAMOST信噪比大于50以上的恒星光谱数据中测量效果非常好 ...

2013

0.0

... 本文采用的是核岭回归(kernel ridge regression, KRR)^[10]算法, 首次将该算法应用在天体光谱参数测量上面, 实验结果表明该方法在天体光谱参数测量方面是可行的 ...

2018

0.0

... 在大数据时代, 数据一般都是高维, 所以共线性^[11]问题不容忽视, 而KRR方法在解决这一问题时具有优势 ...

2018

0.0

... 岭回归虽然放弃了LSM的无偏性, 损失了精度, 但得到的回归系数却能够更加符合实际情况^[12] ...

2018

0.0

... 在数据分析和建模中, 当预测变量高度相关时, 岭回归产生的系数比LSM预测的系数具有更好的稳定性^[13] ...