引用本文
张福才, 汤伟, 孙晓刚. 极小值优化法反演多光谱高温计真温[J]. 光谱学与光谱分析, 2020,40(10): 3130-3135.
ZHANG Fu-cai, TANG Wei, SUN Xiao-gang. Multispectral True Temperature Inversion Based on Multi-Objective Minimum Optimization Principle of Reference Temperature[J]. Spectroscopy and Spectral Analysis, 2020,40(10): 3130-3135.
Doi:10.3964/j.issn.1000-0593(2020)10-3130-06  
Permissions
Copyright©2020, 《光谱学与光谱分析》期刊社
《光谱学与光谱分析》期刊社 所有
极小值优化法反演多光谱高温计真温
张福才1,2, 汤伟1, 孙晓刚2,*
1.陕西科技大学电气与控制工程学院, 陕西 西安 710021
2.哈尔滨工业大学仪器科学与工程学院, 黑龙江 哈尔滨 150001
*通讯联系人 e-mail: qingtengzfc@yeah.net

作者简介: 张福才, 1978年生, 陕西科技大学电气与控制工程学院博士 e-mail: 510132156@qq.com

收稿日期: 2019-06-20
基金: 国家自然科学基金项目(61875046), 陕西科技大学博士科研启动基金项目(2019BJ-48)资助
摘要

多光谱测温法是通过测量多个光谱辐射信息并采用相关的理论与算法反演出辐射体真实温度(真温)的过程。 光谱发射率求解仍然是多光谱测温法的重点和难点, 从理论上必须已知足够多的光谱信息才能获得辐射体的真温。 考虑到实际辐射体在不同光谱和不同温度时的光谱发射率通常是不一致且光谱发射率的求解又是非接触的辐射温度测量中不可回避的问题, 因此, 开展多光谱发射率的求解和真温反演方法的研究具有很强的科学意义和应用价值。 经过半个多世纪的不懈努力与发展, 光谱发射率求解可以概括为四类模型。 一是灰体假设模型, 认为在真温反演过程中光谱发射率是一个常数或其变化可以忽略不计; 二是波长假设模型, 认为在真温反演过程中光谱发射率与波长之间存在一定关系, 可以用含有波长的表达式代替光谱发射率实现真温的反演; 三是真温假设模型, 认为在真温反演过程中光谱发射率与真温之间存在一定的关系, 将光谱发射率与真温之间建立模型并通过迭代方法来实现真温的反演; 四是建立神经网络模型, 通过神经网络的学习实现真温的反演。 基于真温的唯一性, 在对不同假设模型的分析基础上, 试图寻求一种无需假设光谱发射率模型且具有一定通用性的真温反演方法, 开展以多光谱真温反演算法为核心的研究工作。 概述了传统多光谱真温反演理论与方法的特点, 针对现有的多光谱真温反演过程中光谱发射率模型选择复杂性, 提出了一种有约束优化原理的单目标函数极小值的真温反演方法, 这种方法无需假设光谱发射率模型, 将真温的反演问题转变成求解目标函数极小值的优化问题。 借助于用一个黑体炉并且在黑体炉光源输出端口加装光谱透过率已知的滤波器来模拟辐射源, 实现了基于极小值优化法多光谱高温计真温的反演。 与传统的二次测量法相比, 在相同的初始条件下, 与曾经提出的二次测量法相比, 新方法在反演精度上与二次测量法大体相同, 但在反演速度上得到了较大幅度的提高。

关键词: 优化; 多光谱; 发射率; 真温
中图分类号:TH865 文献标志码:A
Multispectral True Temperature Inversion Based on Multi-Objective Minimum Optimization Principle of Reference Temperature
ZHANG Fu-cai1,2, TANG Wei1, SUN Xiao-gang2,*
1. School of Electrical and Control Engineering, Shaanxi University of Science and Technology, Xi’an 710021, China
2. School of Instrument Science and Engineering, Harbin Institute of Technology, Harbin 150001, China
*Corresponding author
Abstract

Multispectral thermometry is a process of retrieving the true temperature of radiators by measuring the information of multispectral radiations and using related theories and algorithms. The solution of spectral emissivity is still the key and difficulty in multispectral thermometry. Theoretically, it is necessary to know enough spectral information to obtain the true temperature of the radiator. Considering that the spectral emissivity of actual radiators at different spectrum and temperatures are usually inconsistent, and the solution of spectral emissivity is an unavoidable problem in non-contact radiation temperature measurement, it is of great scientific significance and application value to carry out the research on the solution of multispectral emissivity and the inversion methods of true temperature. After decades of development, the solution spectral emissivity can be generalized into four types of models. One is the grey body hypothesis model, which considers that spectral emissivity is a constant or its change can be neglected in the process of temperature inversion; the other is the wavelength hypothesis model, which considers that there is a certain relationship between spectral emissivity and wavelength in the process of temperature inversion. Thirdly, the true temperature hypothesis model, which considers that there is a certain relationship between spectral emissivity and true temperature in the inversion process of the true temperature, and establishes a model between spectral emissivity and true temperature and realizes the inversion of true temperature with iteration method; Fourthly, the establishment of a neural network model, which achieve true temperature inversion by the neural learning network. Based on the uniqueness of true temperature and the analysis of different hypothetical models, thethesis tries to find a generaltrue temperature inversion method without the hypothesis of spectral emissivity model and carries out the research work with multispectral true temperature inversion method as the core. The paper summarizes the characteristics of traditional multispectral true temperature inversion theories and methods. In view of the complexity of selecting the spectral emissivity model in the existing multispectral true temperature inversion process, a true temperature inversion method based on the constrained optimization principle of single objective function minimization is proposed. This method does not need to assume the spectral emissivity model and convert the true temperature solution problem into an optimization problem to solve the minimum of the objective function. By using a blackbody furnace and adding a filter with known spectral emissivity at the output port of the blackbody furnace light source to simulate the radiation source, the true temperature inversion of multispectral pyrometer based on minimum optimization method is realized. Compared with the traditional second measurement method, under the same initial conditions and compared with the original second measurement method proposed by the research group, the new method has the same inversion accuracy as the second measurement method, but the inversion speed has been greatly improved.

Keyword: Optimization; Multispectral; Emissivity; True temperature
引言

非接触辐射温度测量作为一种温度测量技术, 由于其不会与被测目标接触, 近些年来, 在诸多方面都有着广泛的应用[1]。 光谱发射率仍然是多光谱测温核心问题, 其求解主要有以下三种方案。 一是波长假设模型, 光谱发射率与波长之间建立模型来实现真温和光谱发射率反演。 经过几十年的发展, 2014年, 杨永军等分析了光谱发射率的阶层与红外波段波长之间的函数关系, 验证了在一定波段内, 建立的光谱发射率的阶层与红外波段波长之间的关系, 实现了波长假设模型的真温反演[2]。 2016年, Zhang等采用维恩公式, 假设某一温度下光谱发射率与波长之间存在线性或非线性关系, 提出光谱识别法的多光谱真温反演算法, 实现了中红外波段真温的反演[3]。 2016年, Liu等将光谱发射率和波长之间建立起多项式函数关系, 采用高光谱图像处理技术完成了乙烯火焰的测量, 采用牛顿迭代法求解, 实现了煤烟火焰温度和光谱发射率的反演[4]。 有报道根据光谱发射率的缓变特性, 假设相邻波长对应的光谱发射率近似相等, 减少了未知数的个数, 实现了真温的反演。 2019年, 张磊等基于多光谱测量理论, 设计采用多通道光电探测器的多光谱测温装置, 系统由钨标准化灯进行标定, 通过测量标准辐射源的温度验证了辐射测温方法的可行性[5]。 二是神经网络假设模型, 2001年, 孙晓刚等提出了一种新的多光谱温度测量数据处理的思路, 全面将神经网络算法引入到了多光谱温度测量领域, 应用神经网络算法对多光谱测量数据进行了处理, 取得了良好效果[6]。 2011年, Khatami等采用三个波长高温计测量了含有煤粉颗粒的火焰温度, 采用二向色滤光片和窄带滤光片实现了热辐射信号的分离, 利用硅光电探测器实现了光电转换, 最后对温度的影响因素二向色滤光片、 窄带滤光片和光电池探测器进行了理论分析[7]。 有研究采用USB 4000型光纤光谱仪得到了多光谱测试数据, 利用神经网络算法对多光谱数据进行了处理, 这种方法无需建立光谱发射率与波长之间的函数关系, 只要经过神经网络学习, 可以实现真温和光谱发射率的反演。 2018年, Vandersteegen等建立新温度测量模型, 通过RBF神经网络测量模型完成了CCD的标定, 建立了高精度的颜色测量方法, 从仿真可知, 这种基于RBF网络的高温测量系统测温算法具有精度高, 适应性强等优点[8]。 这类神经网络模型的反演程序存在一定技术难度, 而且神经网络学习过程需要时间, 因此这种真温反演方法的反演速度总的来说并不高。 三是真温假设模型, 2001年, 从大成等假设光谱发射率与真温之间在一定温度范围内存在某种线性函数关系, 初步提出了二次测量法的理论模型, 完成了相关理论的仿真实验[9]。 2003年后, Song等完善了光谱发射率和真温的假设模型, 通过迭代的方法可以求解出真温和光谱发射率[10]。 2017年, 有报道针对二次测量法反演速度较慢的问题, 深挖了亮度温度模型中内在的、 隐性的普适规律, 提出了一种基于模型约束条件的二次测量法, 这种模型约束条件使二次测量法的反演速度有了普遍的提高, 最大幅度达到了43.45%[11]。

综上所述, 在多光谱真温反演过程中, 通常需要光谱发射率与其他物理量(波长或真温)之间的变化关系才能实现真温的反演, 另外, 如何提高真温和光谱发射率的反演速度以更好地满足实际需要是这种方法亟待解决的问题之一。 本工作的主要目的是寻找一种无需建立光谱发射率与波长之间的数学模型而且反演速度较高的多光谱反演方法。

1 极小值最优化的真温反演原理

当采用多光谱高温计对温度为Trb的黑体炉进行测量时, 多光谱高温计的输入为某一波长λ i时的辐射能量, 输出为电压信号, 其电压Vλ ib可表示为[12]

Vλib=Aλiλi-5eC2λiTrb-1-1(1)

式(1)中, Aλ i是与波长、 光学元件的探测率、 几何尺寸和第一辐射常数有关的检定常数, λ i是相应通道的波长, C2是第二辐射常数, 而对于真温为Tz的待测目标而言, 其输出电压Vλ i可表示为[13]

Vλi=Aλiελiλi-5eC2λiTz-1-1　i=1, 2, …, n(2)

式(1)中, ε λ i是温度Tz时待测目标的光谱发射率, 将式(1)和式(2)相除, 得

VλiVλib=ελieC2λi·Trb-1/eC2λiTz-1(3)

分析式(3), 对于n个通道的多光谱高温计, 可以得到n个测量方程的同时也得到n+1未知数(n个ε λ i和真温Tz), 理论上有无穷多组解。 令TTb= eC2/(λiTrb)-1, 多光谱高温计某一测量通道的真温Tzi可表示为式(4)

Tzi=C2λiln((ελiVλibTTb)/Vλi+1)(4)

1.1 多目标函数

对于每一个光谱通道都可以利用式(4)表示真温。 其中, 光谱发射率是未知数, 由辐射测温的基本理论可知, 光谱发射率随着波长的变化具有渐变的特征, 相邻两个通道表示的真温差不会变化很大, 因此, 取相邻两个通道表示的真温差最小构成一个目标函数, 即式(5)

F1=min((Tz1-Tz2)+(Tz3-Tz4)+(Tz5-Tz6)+(Tz7-Tz8))(5)

对于同一点同一时刻的测量, 真温具有唯一性, 由多光谱高温计不同通道表示的真温分别为Tzi和Tz(i+1), 由于测量中误差的存在, 造成Tzi≠ Tz(i+1), 由误差的相关知识可知, 由不同通道表示的真温标准差越小表示测量的可靠性越强, 测量精度也相对较高, 因此, 采用标准差最小作为一个目标函数, 即式(6)

F2=min∑i=1N(Tzi-T̅)2/N(6)

式(6)中, Tzi为第i通道的表示的真温(K); T̅为多光谱高温计各通道表示真温之和的平均值, T̅=1N∑i=1NTzi, (K); N为高温计测量通道的数量, 下同。

式(5)和式(6)构成了两个目标函数, 依据有约束优化理论, 很难求得真温一个Tz使两个目标函数同时达到极小值, 因此, 只能将满足两个目标函数的近似解或弱有效解时的Tz视为被测目标的真温。

1.2 不等式约束条件

由辐射测温的基本理论可知, 光谱发射率范围都在0和1之间, 如式(7)所示。

0< εi< 1(7)

根据式(4)可知, 真温最大值Tmax可表示为

Tmax=C2λimaxln((ελiminVλibTTb)/Vλimax+1)(8)

式(8)中, λ imin为所有有效波长的最小值, ε λ imin为光谱发射率的最小估计值, λ imax为测量波长的最大值, 再结合式(4), 得

C2λiln((ελiVλibTTb)/Vλi+1)< Tmax(9)

式(9)中, i的取值范围为i=1, 2, …, N, 由式(9)构成了含有真温的不等式约束条件。

2 极小值最优化的真温反演方法的求解

通过上述原理分析, 建立了极小值最优化原理形式与式(10)的多目标优化结构一致。 因此, 可以采用多目标优化函数对极小值最优化原理对真温和光谱发射率进行反演, 多目标优化函数的形式为

V-min{f1(X), f2(X), …, fp(X)}, X∈Rns.t.gj(X)≤0j=1, 2, …, mp≥2m≥1(10)

式(10)中, f1(X), f2(X), …, fp(X)为极小值目标函数, Rn为一个向量组, X为自变量, gj(X)≤ 0为不等式约束条件。 可以使用仿真软件Matlab库函数实现多目标函数极值的求解, 在求解目标函数极值的后可以实现光谱发射率的反演和真温的计算。

3 实验验证

为了检验所提出的算法, 设计了一个简单的装置, 其结构图如图1所示, 在黑体炉和微型光谱仪之间分别插入JB9、

QB18和LB6三种型号的衰减片来模拟辐射源, JB9衰减片的透过率随波长增加逐渐增大, QB18衰减片的透过率随波长增加逐渐减小, LB6衰减片的透过率随波长增加先增加后逐渐减小。 将微型光谱仪采集的多光谱数据通过USB接口传送至计算机。 将黑体炉的温度设定为1 214.5 K, 待其稳定后将多光谱高温计瞄准黑体炉并采集8个通道电压, 这些电压值即为在参考温度Trb=1 214.5 K时的电压数据。 多光谱高温计每一通道的有效波长和各个通道的电压如表1所示。 这些数据将应用于真温和光谱发射率反演中。

图1 实验验证示意图Fig.1 Experimental verification schematic diagram

表1 参考温度下每个测量通道的电压值 Table 1 Voltage of each measurement channel at reference temperature
表2 实际测量中各测量通道的电压值 Table 2 Voltage of each measuring channel in actual measurement

采用极小值最优化的真温反演方法(true temperature inversion method with minimum optimization, IMO)反演真温并记录了反演时间, 如表3所示, 反演的光谱发射率如表4所示。 从表3中两种方法反演的结果的对比可知, 两种方法的求解结果基本相同, 误差都约为1%; 在反演时间上, 二次测量法的反演时间都在50 s以上, 而极小值最优化的真温反演方法的反演时间都小于3 s, 反演速度有了较大幅度的提高。

表3 真温反演结果 Table 3 Inversion results of true temperature
表4 光谱发射率反演结果 Table 4 Inversion results of spectral emissivity

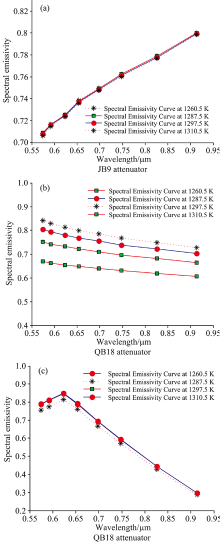
图2为根据光谱发射率绘制的光谱发射率随波长变化的曲线图。 虽然反演的真温值相同, 但每一个真温下光谱发射率的随波长的变化并不一致, JB9衰减片类似一种高通滤波器, QB18衰减片类似一种低通滤波器, LB6衰减片类似一种带通滤波器。

图2 光谱发射率随波长的变化趋势
(a): JB9衰减器; (b): QB18衰减器; (c): LB6衰减器Fig.2 Variation of spectral emissivity with the wavelength
(a): JB9 attenuator; (b): QB18 attenuator; (c): LB6 attenuator

4 结论

提出了一种基于极小值最优化的多光谱真温反演方法, 得到以下几个方面的结论: (1)该方法无需对光谱发射率与波长之间的关系做任何限制, 理论上简化了真温反演的原理; (2)在反演精度上, 与二次测量法大体相当, 相对误差都在1%左右; (3)在反演时间上, 与二次测量法相比, 极小值最优化的多光谱真温反演方法的反演时间都小于3s, 反演速度有了较大幅度的提高。

本研究提出的极小值优化原理的多光谱真温反演方法是一种可行的真温和光谱发射率的反演的方法, 而采用优化思想的真温反演方法很可能成为多光谱真温反演研究的新方向, 其较快的真温反演速度很可能在多点的真温测量中展现出更好的应用前景。

参考文献
[1] Araújo A. Infrared Physics & Technology, 2016, 76: 365. [本文引用:1]
[2] YANG Yong-jun, WANG Zhong-yu, ZHANG Shu-kun, et al(杨永军, 王中宇, 张术坤, 等). Journal of Beijing University of Aeronautics and Astronautics(北京航空航天大学学报), 2014, 40(8): 1022. [本文引用:1]
[3] Zhang L, Dai J M, Yin Z. Chinese Optics Letters, 2015, 13(6): 83. [本文引用:1]
[4] Liu H, Zheng S, Zhou H, et al. Measurement Science & Technology, 2016, 27(2): 025201. [本文引用:1]
[5] ZHANG Lei, CHEN Shao-wu, ZHAO Hai-chuan, et al(张磊, 陈绍武, 赵海川, 等). Chinese Optics(中国光学), 2019, 12(2): 289. [本文引用:1]
[6] SUN Xiao-gang, HE Jin, DAI Jing-min, et al(孙晓刚, 何瑾, 戴景民, 等). Journal of Harbin Institute of Technology(哈尔滨工业大学学报), 1998, 30(6): 1. [本文引用:1]
[7] Khatami R, Levendis Y A. Combustion and Flame, 2011, 158(9): 1822. [本文引用:1]
[8] Vand ersteegen M, Beeck K V, Goedemé T. Real-Time Multispectral Pedestrian Detection with a Single-Pass Deep Neural Network. International Conference Image Analysis and Recognition. Springer, Cham, 2018: 419. [本文引用:1]
[9] CONG Da-cheng, DAI Jing-min, SUN Xiao-gang, et al(丛大成, 戴景民, 孙晓刚, 等). Journal of Infrared and Millimeter Waves(红外与毫米波学报), 2001, 20(2): 97. [本文引用:1]
[10] Song Y, Sun X, Tang H. Chinese Optics Letters, 2007, 5(8): 457. [本文引用:1]
[11] Liang Mei, Sun Bojun, Sun Xiaogang, et al. International Journal of Thermophysics, 2017, 38(3): 35. [本文引用:1]
[12] DAI Jingmin. Theory and Practice of Multi-spectral Thermometry. Beijing: Higher Education Press, 2002. [本文引用:1]
[13] SUN Xiao-gang, DAI Jing-min, WANG Xue-feng, et al(孙晓刚, 戴景民, 王雪峰, 等). Journal of Infrared and Millimeter Waves(红外与毫米波学报), 2003, 22(2): 141. [本文引用:1]