引用本文
张鹏, 孙兰香, 于海斌, 齐立峰, 曾鹏. Voigt函数拟合的LIBS谱线自吸收校正方法在磷矿镁元素分析中的应用[J]. 光谱学与光谱分析, 2020,40(1): 266-270.
ZHANG Peng, SUN Lan-xiang, YU Hai-bin, QI Li-feng, ZENG Peng. A LIBS Spectral Self-Absorption Correction Method Using Voigt Profile Fitting for the Application of Magnesium Analysis in Phosphorus Ore[J]. Spectroscopy and Spectral Analysis, 2020,40(1): 266-270.
Doi:10.3964/j.issn.1000-0593(2020)01-0266-05  
Permissions
Copyright©2020, 《光谱学与光谱分析》期刊社
《光谱学与光谱分析》期刊社 所有
Voigt函数拟合的LIBS谱线自吸收校正方法在磷矿镁元素分析中的应用
张鹏1,2,3,4, 孙兰香1,2,3,*, 于海斌1,2,3, 齐立峰1,2,3, 曾鹏1,2,3
1. 中国科学院沈阳自动化研究所, 辽宁 沈阳 110016
2. 中国科学院机器人与智能制造创新研究院, 辽宁 沈阳 110016
3. 中国科学院网络化控制系统重点实验室, 辽宁 沈阳 110016
4. 中国科学院大学, 北京 100049
*通讯联系人 e-mail: sunlanxiang@sia.cn

作者简介: 张 鹏, 1986年生, 中国科学院沈阳自动化研究所博士研究生 e-mail: zhangpeng@sia.cn

收稿日期: 2018-11-12
基金: 国家自然科学基金项目(61473279), 国家重点研发计划项目(2016YFF0102502)资助
摘要

MgO含量是磷矿浮选过程中最为关注的指标之一。 实现浮选过程中MgO含量的快速检测, 对于优化浮选过程、 提高效率、 降低成本有着非常实际的意义。 因此, LIBS技术被引入到了磷矿中镁元素含量的分析。 常用于LIBS分析的Mg元素特征谱线(如Mg Ⅱ 279.6 nm, Mg Ⅱ 280.3 nm, Mg Ⅰ 285.2 nm)多为共振线, 谱线强度易受自吸收效应影响, 导致谱峰强度下降, 影响分析准确性。 提出一种基于近似Voigt函数的拟合方法: 首先通过近似函数对Voigt函数进行简化; 再通过低含量样本确定谱峰中心和理想条件下的半峰宽; 进而通过计算谱峰所在区域线型的斜率, 确定用于拟合的谱翼区域; 最终通过对谱峰两翼受自吸收效应影响较小的光谱进行拟合, 得到更接近理论线型的谱线。 在定量分析磷矿样品中的镁元素含量应用中, 使用拟合后的Mg Ⅰ 285.2 nm谱线区域面积作为分析谱线强度, 以拟合的Si 288.2 nm谱线区域面积作为参考谱线强度, 使用内标法对镁元素含量进行了标定。 对比未拟合直接内标的方法, 该方法的标定确定系数( R2)由0.923提升至0.998, 均方根误差(RMSE)和平均相对误差(ARE)分别由0.96, 38.65%下降到0.16, 2.79%, 说明该方法使磷矿镁元素定量分析的整体测量准确性得到了有效的提升。

关键词: 激光诱导击穿光谱; 定量分析; 谱线拟合; 自吸收效应; 磷矿
中图分类号:O657.3 文献标志码:A
A LIBS Spectral Self-Absorption Correction Method Using Voigt Profile Fitting for the Application of Magnesium Analysis in Phosphorus Ore
ZHANG Peng1,2,3,4, SUN Lan-xiang1,2,3,*, YU Hai-bin1,2,3, QI Li-feng1,2,3, ZENG Peng1,2,3
1. Shenyang Institute of Automation, Chinese Academy of Sciences, Shenyang 110016, China
2. Institutes for Robotics and Intelligent Manufacturing, Chinese Academy of Sciences, Shenyang 110016, China
3. Key Laboratory of Network Control System, Chinese Academy of Sciences, Shenyang 110016, China
4. University of Chinese Academy of Sciences, Beijing 100049, China
*Corresponding author
Abstract

The concentration of MgO is one of the most important parameters in the phosphate ore flotation. The fast detection of the concentration of MgO has great significance for the optimization of the flotation, the improvement of the efficiency and the reduction of the cost. Therefore, LIBS (Laser Induced Breakdown Spectroscopy) is introduced into the analysis of Mg in phosphate. But the common used strong lines of Mg (Mg Ⅱ 279.6 nm, Mg Ⅱ 280.3 nm, Mg Ⅰ 285.2 nm) are resonance lines in LIBS analysis. For the effect of the self-absorption, the spectral intensity of the resonance line is lower than the theoretical value, and this intensity reduction will reduce the accuracy of the analysis. In this work, a method based on an approximate function of Voigt profile was proposed. Firstly, simplified the Voigt profile function with the approximate function; secondly, determined the center of the spectral line and the full width at half maximum (FWHM) under ideal conditions with the low concentration samples; then, determined the wing area for fitting by calculating the slope of the spectral area near the spectral peak; finally, obtained the fitting profile closer to the theoretical one, by fitting the approximate function with the wing area selected above. In the application of the quantitative analysis of Mg in phosphate ore, the internal standard method was used forthe calibration. The fitting spectral areas of Mg Ⅰ 285.2 nm and Si Ⅰ 288.2 nm were chosen as the analytical line intensity and the reference line intensity, respectively. Comparing the internal standard method without fitting, the determination coefficient ( R2) with the proposed method was improved from 0.923 to 0.998; the root-mean-square error (RMSE) and the average relative error (ARE) were reduced from 0.96 and 38.65% to 0.16 and 2.79%, respectively. The calibration results proved that with the proposed method, the measurement accuracy can be improved significantly for the application of magnesium analysis in phosphorus ore.

Keyword: Laser induced breakdown spectroscopy (LIBS); Quantitative analysis; Spectral profile fitting; Self-absorption; Phosphorus ore
引 言

我国磷矿资源总体储量丰富, 但贫矿多、 富矿少, 存在中低品位的矿石、 难选磷矿资源多等问题。 镁元素大部分以白云石的形式存在于磷矿中, 在磷的富集成矿过程中起到提高天然磷在液相中浓度的作用。 因此在磷矿原矿中, 氧化镁含量通常都超过1.5%, 最高可能超过10%, 但过高的氧化镁含量会影响湿法磷酸及后续磷产品的生产。 因此, 磷矿脱镁成为了高镁磷矿开发利用的一项必要工作。 MgO含量, 与P2O5含量以及磷的回收率一样, 成为浮选过程中最为关注的指标之一。

激光诱导击穿光谱(LIBS), 以样品预处理简单, 可同时检测多种元素, 对各种元素均有较高的检出限, 分析时间快速固定等特点, 成为工业现场实时在线检测应用中备受关注的分析技术[1, 2, 3, 4, 5], 被誉为分析化学领域的“ 未来之星” 。

应用LIBS对镁元素的分析研究, 主要集中在镁在样品中属于微量、 痕量元素的情况[6, 7, 8]。 在我们之前的工作[9]中, 分析了铝合金样品中的硅、 铁、 铜、 锰和镁元素(其中镁元素最大含量0.51%), 使用共振线Mg Ⅱ 280.3 nm作为分析线时, 分析结果明显受到了自吸收效应的影响。 Sabri等对比分析了不同实验条件下激光诱导等离子体中Al元素特征谱线受自吸收效应的影响[10]; 赵法刚等提出了一种基于自吸收量化的激光诱导等离子体表征方法[11], 通过弱化计算过程与谱线强度的相关性, 减小自吸收效应影响; Yun等使用Lorentz函数拟合的方法对陶瓷原料土壤中的K元素含量进行了分析[12], 结果的准确性得到了一定程度的提升。

我们提出了一种基于近似Voigt函数的、 针对谱线两翼部分轮廓的谱线拟合方法。 通过该方法拟合后的特征谱线, 可以更好的还原未受自吸收效应影响的原始谱线轮廓。 将方法应用于磷矿粉末压样中镁元素(含量范围0.5%~10.5%)的定量分析, 分析含量的确定系数(R2)可以由0.923提升到0.998。

1 实验部分
1.1 仪器及参数

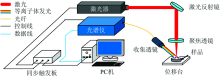
实验系统示意如图1所示。 激光器采用镭宝光电的nimma400系列调Q纳秒Nd:YAG激光器, 实验中输出脉冲能量约25 mJ; 激光聚焦透镜为焦距50 mm的石英平凸透镜; 等离子体发光的收集透镜为焦距35 mm的石英平凸透镜, 收集方式为45° 方向侧向收集; 光谱仪选择海洋光学的LIBS2500+, 检测光谱范围200~980 nm, 光学分辨率0.1 nm, 延时1 μ s, 积分时间1 100 μ s。

图1 实验系统示意图Fig.1 The schematic diagram of the experimental system

1.2 样品与数据

样品是北京矿冶研究总院提供的10种磷矿粉末, Mg元素含量的ICP测量结果如表1所示。 使用10 MPa压力进行压样, 每个样品选择20个点进行实验, 每个点进行15次激光击打, 使用前5个激光脉冲进行清洁, 取后10个脉冲得到的光谱的平均值用于分析。

表1 样品Mg元素含量表(%) Table 1 The concentration of Mg in the samples (%)
2 结果与讨论
2.1 近似Voigt函数拟合

对于典型的激光诱导击穿光谱而言, 自然谱线在Doppler展宽、 碰撞展宽、 Stark展宽和仪器展宽等因素的综合影响下, 最终的谱线轮廓是Lorentz函数与Gauss函数的卷积形式, 称为Voigt函数[13, 14], 表达式为

LV(λ)=LG(λ)LL(λ)=4ln2π1ΔλG·aπ∫-∞∞exp(-x2)a2+(v-x)2dx(1)

其中 v=2ln2λ-λ0ΔλG, a=ln2ΔλLΔλG, λ表示波长, λ0表示特征谱线中心位置, ΔλG和ΔλL分别代表Gauss函数和Lorentz函数展宽线型的半峰宽。 由于该表达式过于复杂, 不利于直接对其进行拟合。 Wertheim等提出了一种近似的表达形式[15]

f(λ, [α, λ0, ΔλV, η])=α(ηΔλV2ΔλV2+4(λ-λ0)2+(1-η)exp-4(λ-λ0)2ln2ΔλV2)(2)

其中α 是谱峰高度, λ 0表示特征谱线中心位置, Δ λ V是半峰宽, η 是Lorentz-Gauss比例系数, 0≤ η ≤ 1。 通过拟合参数α , λ 0, Δ λ V和η , 就可以确定Voigt线型的近似函数。

2.2 部分数据拟合近似Voigt函数

在受自吸收效应影响严重的特征谱线区域, 采集到的光谱中特征谱线中心位置附近的强度变小。 此时, 直接使用整个特征谱线存在的波长范围内的全部数据进行拟合, 既无法反应特征谱线的真实强度, 也无法得到较好的拟合效果。 因此, 考虑只通过谱线轮廓两侧未受自吸收效应影响的数据, 拟合谱线轮廓。

将各样品在283.2~287.2 nm谱段的光谱强度进行归一化, 然后用式(3)计算各个位置的近似斜率, In和λ n分别代表第n个位置的谱线强度和波长。

Slopen=In-In-1λn-λn-1+In+1-Inλn+1-λn×0.5(3)

各样品光谱在285 nm附近的近似斜率值如图2所示。 可以看出: 由于Mg 285.2 nm特征谱线的存在, 斜率在284.7~285.5 nm范围内不为0; 在284.94~285.22 nm的范围内, 由于受到自吸收效应影响不同, 各样品的光谱线型的斜率有明显的差异。 因此, 将谱段283.2~284.94和285.22~287.2 nm作为参与拟合的谱段范围, 忽略284.94~285.22 nm的光谱, 以减小自吸收效应对拟合谱线的影响。

图2 不同样品光谱在285 nm附近的斜率Fig.2 The spectral slopes of different samples near 285 nm

认为Mg元素含量相对较小的1#— 4#样品未受自吸收效应影响或受自吸收效应影响较小。 使用式(2)表示的近似Voigt函数, 针对283.2~287.2 nm范围内的全部光谱数据进行拟合, 得到4组拟合参数[α , λ 0, Δ λ V, η ]1— 4, 4组参数的均值记作[ α̅, λ̅0, Δ λ̅V, η̅]。 进一步认为在激光器、 光谱仪等仪器的实验参数不变, 其他实验条件也保持一致的情况下, 各样品对应的谱峰中心波长和Lorentz-Gauss比例系数应该相同, 都等于 λ̅0和 η̅; 同时, 由于连续背景和其他谱线的影响, 增加一个连续背景强度偏移量β 。 最终得到新的拟合公式

f(λ, [α, ΔλV, β])=α(η̅ΔλV2ΔλV2+4(λ-λ̅0)2+(1-η̅)exp-4(λ-λ̅0)2ln2ΔλV2)+β(4)

使用式(4)对10个样品原始光谱中283.2~284.94, 285.22~287.2 nm范围内的数据进行拟合, 情况如图3所示。 可以看出, 284.94~285.22 nm以外的其他位置的谱线轮廓得到了很好的拟合, 而284.94~285.22 nm谱段内拟合曲线的强度更高也更符合没有自吸收现象的谱线强度情况。

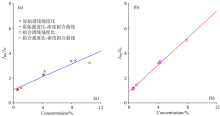
图3 近似Voigt函数部分数据拟合结果Fig.3 The approximate Voigt profile fitting results with partial spectral data

2.3 定量分析结果对比

由于样品压片表面情况很难保证一致, 因此选择了Mg 285.2 nm特征谱线作为分析线, Si 288.2 nm特征谱线作为参考线, 进行内标法定量分析。 原始谱线比和近似Voigt函数部分数据拟合后的谱线比与Mg元素含量的拟合结果分别如图4(a)和(b)所示, 具体的确定系数(R2)、 均方根误差(RMSE)和平均相对误差(ARE)如表2所示。 对于原始谱线强度比, 由于Mg元素特征谱线自吸收现象严重, 所以Mg/Si谱线强度比较小, 标定结果的确定系数仅为0.923, 均方根误差0.96, 平均相对偏差高达38.65%。 使用近似Voigt函数对部分谱线数据拟合, 拟合后的谱线半峰宽区域面积作为强度, 从一定程度上校正了谱线的自吸收, 得到的谱线强度比较大, 标定结果的确定系数达到0.998, 均方根误差下降到0.16, 平均相对偏差下降到2.79%。

图4 内标法标定结果对比Fig.4 The comparison of the calibration results with the internal standard method

表2 内标法标定结果比较 Table 2 The comparison results of the internal standard method calibration
3 结 论

针对磷矿原矿和尾矿中镁元素含量较高, LIBS特征谱线受自吸收效应影响严重的问题, 提出通过部分数据拟合近似Voigt函数的方法, 来消除自吸收效应对谱线强度的影响。 通过该方法拟合后的谱线, 更符合原始谱线的Voigt线型。 同时, 使用拟合后的Mg Ⅰ 285.2 nm谱峰半峰宽面积和Si Ⅰ 288.2 nm谱峰半峰宽面积的比值标定镁元素含量, 确定系数可由0.923提升到0.998, 均方根误差由0.96下降到0.16, 平均相对误差由38.65%下降到2.79%, 标定的准确程度得到了较大的提升。

参考文献
[1] Afgan M S, Hou Z Y, Wang Z. Journal of Analytical Atomic Spectrometry, 2017, 32(10): 1905. [本文引用:1]
[2] WANG Qian-qian, ZHAO Yu, LU Xiao-gang, et al(王茜蒨, 赵宇, 卢小刚, 等). Spectroscopy and Spectral Analysis(光谱学与光谱分析), 2017, 37(8): 2430. [本文引用:1]
[3] Shen M, Li C M, Na D, et al. Journal of Analytical Atomic Spectrometry, 2018, 33(4): 658. [本文引用:1]
[4] Matsumoto A, Ohba H, Toshimitsu M, et al. Spectrochimica Acta Part B: Atomic Spectroscopy, 2018, 142: 37. [本文引用:1]
[5] Xin Y, Sun L X, Yang Z J, et al. Frontiers of Physics, 2016, 11(5): 1. [本文引用:1]
[6] Costa V C, De Babos D V, De Aquino F W B, et al. Food Analytical Methods, 2017, 11(7): 1886. [本文引用:1]
[7] Rehan I, Rehan K, Sultana S, et al. Applied Physics B, 2018, 124(5): 76. [本文引用:1]
[8] LUAN Ya-ge, LU Cui-ping, HU Hai-ying, et al(栾亚阁, 鲁翠萍, 胡海瀛, 等). Applied Laser(应用激光), 2015, (6): 708. [本文引用:1]
[9] Zhang P, Sun L X, Yu H B, et al. Journal of Analytical Atomic Spectrometry, 2017, 32(12): 2371. [本文引用:1]
[10] Sabri N M, Haider Z, Tufail K, et al. Physics of Plasmas, 2018, 25(7): 9. [本文引用:1]
[11] Zhao F G, Zhang Y, Zhang L, et al. Acta Physica Sinica, 2018, 67(16): 5. [本文引用:1]
[12] Tang Y, Guo L, Tang S, et al. Appl. Opt. , 2018, 57(22): 6451. [本文引用:1]
[13] YIN Zeng-qian, WU Chen, GONG Wan-yu, et al(尹增谦, 武臣, 宫琬钰, 等). Acta Physica Sinica(物理学报), 2013, (12): 212. [本文引用:1]
[14] LIU Ming-hui, DONG Zuo-ren, XIN Guo-feng, et al(刘铭晖, 董作人, 辛国锋, 等). Chinese Journal of Lasers(中国激光), 2017, (5): 255. [本文引用:1]
[15] Wertheim G K, Butler M A, West K W, et al. Review of Scientific Instruments, 1974, 45(11): 1369. [本文引用:1]