作者简介: 刘焕军, 1981年生, 东北农业大学资源与环境学院副教授 e-mail: huanjunliu@yeah.net
土壤反射光谱综合反映了土壤的理化性质和内部结构, 高光谱遥感已被用于基于土壤反射光谱特性的土壤分类。 已有研究一般利用土壤反射光谱一阶微分主成分作为输入量进行光谱分类模型构建, 但主成分数据缺乏物理意义, 且缺乏对比性、 适用范围也有限。 与反射率一阶微分数据相比, 基于去包络线提取具有明确物理意义的特征参数, 能够提高土壤分类的精度, 并寻找到一种高精度土壤分类模型。 选取吉林省农安县的四种典型土壤(风砂土、 草甸土、 黑土、 黑钙土), 将采集后的土壤样本进行风干、 研磨、 过2 mm筛处理, 采用ASD FiledSpec®3便携式光谱仪对处理后的土壤样本的可见光近红外光谱区进行测试, 从而获得土壤样本的光谱数据。 对光谱数据进行九点平滑、 10 nm重采样处理进行降噪, 将处理后的数据分别进行一阶微分主成分以及去包络线处理。 利用土壤样本的去包络线提取光谱特征参数。 以一阶微分主成分数据和光谱特征参数为输入量分别代入Logistic聚类模型(LR)、 人工神经网络聚类模型(ANN)、 K-均值聚类模型(K-means)。 首先明确了不同土类之间的反射光谱曲线、 去包络线的差异大小, 以及相同土壤的反射率曲线、 去包络线进行土壤分类的优劣, 并且在去包络线的基础上提取能够区分不同土类的光谱特征参数; 其次, 比较一阶微分主成分与光谱特征参数作为输入量时, 三种光谱分类模型精度差异并分析不同模型精度差异的原因。 结果表明: (1)四种土壤的反射光谱曲线差异较小, 去包络线可以极大的增强四种土壤在430~1 210 nm之间的光谱差异, 并在去包络线的基础上构建具有明确物理意义的光谱特征参数。 (2)将一阶微分主成分和光谱特征参数分别代入三种聚类模型可知, 以光谱特征参数为输入量的土壤光谱分类模型均超过了以一阶微分主成分为输入量的模型精度, 由于光谱特征参数保留了原数据的物理意义、 更准确的体现了不同土壤类型之间的差异性, 而一阶微分主成分数据带有一定的模糊性不同范围之间缺乏对比性, 在土壤分类中以光谱特征参数作为输入量更具有优势。 (3)在三类土壤分类模型中, LR的分类精度最高为76.67%, Kappa系数为0.56; ANN的分类精度中等为72.50%, Kappa系数为0.48; K-means的分类精度最低, 只有65.00%, Kappa系数为0.33。 研究成果可为土壤精细制图、 以及土壤分类仪器的研制提供技术支持。
The soil reflectance spectrum curve reflects the physical and chemical properties and internal structure of the soil. Hyperspectral remote sensing technology has been used to classify soil based on the soil reflectance spectrum characteristics. The first order differential principal component of soil reflectance spectrum is generally used to construct the spectral classification model, but the principal component data is lack of physical significance, contrast and limited scope of application. Compared with the first-order differential reflectivity data, the extraction of the characteristic parameters based on the de-enveloping line can improve the accuracy of soil classification and find a high-precision soil classification model. In this study, four typical soils (wind-sand soil, meadow soil, calcareous soil) were selected in Nong’an County, Jilin Province. The collected soil samples were dried, ground and treated by 2mm sieve. ASD FiledSpec®3 portable spectrometer was used to measure the visible near infrared spectrum of the treated soil samples, and the spectral data of the soil samples were obtained. The spectral data were smoothed by nine points, the noise was reduced by 10nm resampling, and the processed data were processed by the first order differential principal component and the de-enveloping line respectively. The spectral characteristic parameters were extracted by using the continuum removed line of soil samples. The first order differential principal component data and spectral characteristic parameters were input into Logistic clustering model, artificial neural network clustering model and K-means clustering model respectively. In this paper, the reflectance spectra of different soils, the difference of the envelope, the reflectivity curve of the same soil, and the advantages and disadvantages of the soil classification are determined. And the spectral characteristic parameters which can distinguish different soil types are extracted on the basis of de-enveloping line. Secondly, when the first order differential principal component is compared with the spectral characteristic parameter as input, the accuracy differences of the three spectral classification models are compared and the reasons for the difference in the accuracy of different models are analyzed. The results showed that: (1) The difference of the reflectance spectra of the four soils was small, and the spectral difference between the four soils could be greatly enhanced by the continuum removedline. The spectral characteristic parameters with clear physical meaning are constructed on the basis of the de-enveloping line. (2) The first order differential principal component and spectral characteristic parameters are introduced into the three clustering models respectively. The soil spectral classification model with spectral characteristic parameters as input is more accurate than that of the first order differential principal component model, because the spectral characteristic parameters retain the physical meaning of the original data. More accurately reflects the differences between different soil types, and due to the fact that the first order differential principal component data have a certain degree of fuzziness and are lack of contrast between different ranges, it is more advantageous to use spectral characteristic parameters as input in soil classification. (3) Among the three soil classification models, the Logistic clustering model has the highest classification accuracy of 76.67% kappa coefficient of 0.56; the average classification accuracy of the artificial neural network model is 72.50% and the Kappa coefficient is 0.48 K-mean clustering model has the lowest classification accuracy, only 65.00% . And Kappa coefficient is 0.33. The research results can provide technical support for fine mapping of soil and the development of soil classification instrument.
精确的土壤分类模型的构建, 可为实现一种低成本、 快速、 全面的土壤分类方法提供理论依据, 并且可为土壤制图、 以及土壤分类仪器的研制提供技术支持[1]。 土壤光谱反射率是土壤理化特征和内在结构的综合反映[2, 3], 已有大量研究利用土壤反射光谱数据测定土壤有机质、 水分等理化性质, 以及进行土壤分类[4, 5, 6]。
根据土壤反射光谱曲线进行土壤分类的研究可分为两种, 第一种是根据土壤反射光谱曲线的形状特征与其理化性质的关系进行土壤分类, 未与传统土壤分类体系保持一致。 如Condit早在20世纪70年代运用美国的36个州的160土壤样品的反射光谱曲线, 根据不同曲线的形状特征, 将反射光谱曲线分为三大类[7]; 史舟等对土壤光谱数据进行一阶微分、 主成分分析, 运用模糊k-means方法计算最佳分类数目, 最后将中国土壤反射光谱数据分为五类[8]。 第二种是将土壤反射光谱分类与传统土壤分类统一。 如刘焕军等对高光谱反射数据进行去包络线处理并提取反射光谱特征指标, 将特征指标作为输入量建立神经网络模型, 模型的分配精度可达到60%以上。 李丹等对选用的广东省215个稻田土壤样本数据进行S-G一阶导数, 将处理后的数据作为输入量代入支持向量机(SVM)分类, 分配精度高达59%[9]。 Vasques等对测得的不同土层的291个土样的光谱数据利用主成分分析和多元线性回归法进行土壤分类, 结果显示土纲级别分类精度为67%[10]。
土壤光谱分类模型主要有LR, ANN, K-means和SVM等, 都获得了较高的分类精度。 Bu等运用土样的剖面特殊理化性质已知值结合SVM的方法进行分类, 证明了在土壤样本数据少的情况下具有优势, 而在处理大样本数据却存在一些问题[11]。 K-means被称为经典算法之一, 在处理大样本数据时精度较高[12], LR和ANN是自动非线性分类模型, 结果直观, 命名清晰性高, 并且分类精度明显提高[13]。
以上大部分研究运用主成分分析对数据进行降维处理, 再将降维后的数据作为输入量进行分类, 但主成分分析数据并没有实际的物理意义, 不同的研究结果之间没有可比性。 本研究主要解决以下问题: 寻找能够代表土壤反射光谱特征、 并且具有明确物理意义的特征参数。 比较输入量为一阶微分主成分与光谱特征参数的光谱分类模型精度差异。 最后, 建立高精度的土壤反射光谱分类模型。
根据全国第二次土壤普查图, 在农安县采集240个0~20 cm耕层土壤, 土壤类型分别为风砂土(21个)、 草甸土(54个)、 黑土(21个)、 黑钙土(144个)。 首先将采集的土样平铺在通风的地方进行风干处理, 然后对风干后的土样进行研磨, 最后将研磨后的土样过2 mm筛。
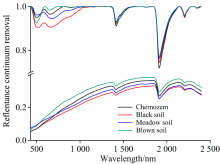
将经过处理后的土壤进行光谱测试。 采用ASD FieldSpec® 3便携式光谱仪, 在其光谱范围内(350~2 500 nm)进行采样。 具体光谱测试步骤见[14]。 将测得的数据进行九点平滑、 10 nm重采样, 对重采样后的数据进行一阶微分、 提取主成分(提取四个主成分, 累计贡献率达到98.96%)以及去除包络线处理(图1)。
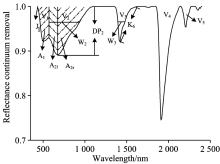
选择准确的输入量和阈值是进行高精度土壤分类的基础。 将反射光谱数据进行去包络线处理后, 从中提取反射光谱特征参数(见图2): 两个吸收谷(V1和V2), 吸收谷的边界为吸收谷两端斜率为0的地方, 吸收谷(V1和V2)主要是由于土壤有机质、 土壤机械组成引起的, 吸收谷(V3, V4和V5)是土壤中所含有的水分引起的, 所以依据前两个吸收谷可以很好的进行土壤分类; 吸收谷面积记为A(吸收谷的左半部分记为l, 右半部分记为r; 第一个谷的左半部分面积记为A1l, 右半部分面积记为A1r)、 谷底位置记为P、 吸收谷肩部的位置记为J、 波段间斜率记为K、 吸收谷的宽度记为W、 吸收谷的对称度记为D、 吸收谷深度记为DP(见图2)。 吸收谷面积A为从吸收谷的左肩开始计算, 用1减去每隔10 nm波长所对应的去包络线的值再乘以10, 反复计算到吸收谷的右肩, 将计算后的数值加和即为该吸收谷的面积; 吸收谷的位置P为某吸收谷去包络线最低时所对应的波长; 吸收谷肩部J为某吸收谷左右两边去包络线值最高所对应的波长; 波段间斜率K为两波长对应去包络线之间的差值与这两波长的差值的比值; 吸收谷高度DP为1减去某一波长对应的去包络线值; 吸收谷宽度W为在某一吸收谷高度一半时, 该吸收谷两侧波长差值。
对农安四种典型土壤分别做10 nm重采样、 去包络线处理(见图1)。 该图上半部分为4种土壤(黑土、 黑钙土、 风砂土、 草甸土)的去包络线, 下半部分为4种土壤的反射光谱曲线。 从图中可以看出, 反射光谱曲线在不同的土类中差异较小, 仅可以看出在整体上反射光谱曲线由大到小排列依次为风砂土、 黑钙土、 草甸土、 黑土, 这是由于农安县气候变化不大以及母质差异较小导致的。
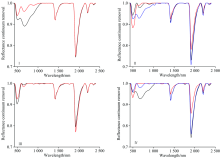
仅根据土壤反射光谱曲线的形状去分析不同土壤之间的差异是很困难的, 去包络线可以大大提高近红外波段(430~2 400 nm)吸收特征, 有利于分析和处理不同类型的土壤反射光谱曲线。 黑土的反射光谱曲线V1与V2的最低点所对应的去包络线值是4类土样中最低的, 并且A1小于A2, V1与V2的深度与土壤有机质的含量成正相关; 在430~590 nm之间, 绝大多数的黑土的斜率都是负值; 在波段660~810 nm内, 黑土的斜率是最低的[见图3(a)]。 黑钙土与黑土相比, 黑钙土的V1与V2的最低点所对应的去包络线值较高, 并且A1大于A2, 与黑土相反; 波段430~590 nm, 大多数的黑钙土的斜率为0, 在590 nm处去包络线的值为1[见图3(b)]。 风砂土与黑土、 黑钙土相比, 有较大的差别, 风砂土的第一个谷的形状很规则, 左右是对称的形状而且谷的宽度很窄; 该土样的A1大于A2, A2的面积多小于2.5, 可以很明显的与其他土类区分出来; 风砂土在波段430~590 nm的斜率都为0, 并且第一个谷的右边界多位于600 nm处, 有少量的位于590 nm处[见图3(c)]。 草甸土的反射光谱曲线种类较多, 与黑土、 黑钙土、 风砂土的光谱曲线都有相似之处, 称这种特性为“ 向邻性” [14][见图3(d)]。
将一阶微分主成分和光谱特征参数作为输入量分别代入LR, ANN和K-means中得到结果见表1。 三种分类模型中, 均以光谱特征参数作为输入量的模型精度大于以一阶微分主成分作输入量的模型精度, 证明了光谱特征参数在土壤分类中更具有优势。 以一阶微分主成分作为输入量时, LR的精度优于ANN和K-means模型。 以光谱特征参数作为输入量时, LR的分类效果最好, 精度为76.67%, Kappa系数为0.56; ANN的分类效果中等, 精度为72.59%, Kappa系数为0.48; K-means的分类效果最差, 精度为65.00%, Kappa系数仅为0.33。
| 表1 基于三种模型与不同输入量的土壤光谱分类精度 Table 1 Soil classification accuracy of different inputs based on three classification models |
目前, 大部分研究是运用反射率或一阶微分的主成分作为输入量进行土壤分类[8, 10, 11]。 以反射率一阶微分主成分作为输入量, 首先得保证前几个主成分的累计贡献率达到一个较高的水平; 其次, 主成分后的数据带有一定的模糊性, 没有原始数据的含义清楚、 确切。 而以光谱特征参数作为输入量时, 不仅保留原有的物理意义、 提取过程简单、 更准确的代表了不同土类之间的差异, 各光谱特征参数均受特定的土壤理化性质的影响, 因此, 模型的分类精度及稳定性更高。 本研究结论是否适用于其他地区有待进一步验证。
当提取特征参数较多, 且取值无规律时, LR模型是有优势的, 它计算每个土壤样本被分到不同土类的概率, 概率最高类别作为该土样的类别。 ANN模型在分类时, 将每个特征都转为数值, 将推理过程变为数值计算, 在此过程中将会丢失大量的原始信息, 从而造成精度的下降。 K-means模型在分类时需要设定分类数目, 而本研究是将土壤反射光谱分类与传统土壤分类统一, 分类数目是固定的, 势必造成精度的下降。
利用农安县土壤反射光谱数据, 进行一阶微分主成分及去包络线提取光谱特征参数处理, 将一阶微分主成分和光谱特征参数作为输入量分别代入LR, ANN, K-means模型中, 进行土壤分类研究, 得到以下结果:
(1)土壤反射光谱曲线很难显示出不同土类之间的差异, 而去包络线可极大的增加土壤430~1 210 nm吸收特征并降低对其他因素的敏感性, 并在去包络线的基础上提取具有明确物理含义的特征参数。
(2)在LR, ANN和K-means模型中, 以特征参数作为特征参数的土壤分类精度均高于反射率一阶微分主成分的精度, 证明特征参数在土壤分类中更具有优势。
(3)将特征参数带入三种聚类模型中, LR模型分类精度最高为76.67%, Kappa系数为0.56; ANN模型分类精度较高; K-means模型精度最低。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|