引用本文
陈颖, 邸远见, 唐心亮, 崔行宁, 高新贝, 曹景刚, 李少华. 基于BiPLS结合SiPLS的组合权值COD浓度预测模型[J]. 光谱学与光谱分析, 2019,39(7): 2176-2181.
CHEN Ying, DI Yuan-jian, TANG Xin-liang, CUI Xing-ning, GAO Xin-bei, CAO Jing-gang, LI Shao-hua. Combination Weight COD Concentration Prediction Model Based on BiPLS and SiPLS[J]. Spectroscopy and Spectral Analysis, 2019,39(7): 2176-2181.
Doi:10.3964/j.issn.1000-0593(2019)07-2176-06  
Permissions
Copyright©2019, 《光谱学与光谱分析》期刊社
《光谱学与光谱分析》期刊社 所有
基于BiPLS结合SiPLS的组合权值COD浓度预测模型
陈颖1, 邸远见1, 唐心亮2,*, 崔行宁1, 高新贝1, 曹景刚1, 李少华3
1. 燕山大学电气工程学院, 河北省测试计量技术及仪器重点实验室, 河北 秦皇岛 066004
2. 河北科技大学信息科学与工程学院, 河北 石家庄 050018
3. 河北先河环保科技股份有限公司, 河北 石家庄 050000
*通讯联系人 e-mail: tangxinliang@hebust.edu.cn

作者简介: 陈 颖, 女, 1980年生, 燕山大学电气工程学院教授 e-mail: chenying@ysu.edu.cn

收稿日期: 2018-06-08 接受日期: 2018-10-27
基金: 国家自然科学基金项目(61201112, 61475133), 河北省自然科学基金项目(F2016203188), 中国博士后基金项目(2018M630279)和河北省高等学校科学技术研究项目(ZD2018243)资助
摘要

水体中过高浓度的有机物含量危害巨大, 不仅会造成严重的环境污染, 而且危害人类身体健康, 传统化学法检测水体化学需氧量(COD)的步骤繁琐且时效性差, 不利于水体中COD的快速定量检测。 针对这些问题, 提出了一种将紫外光谱与组合权值模型相结合的快速定量检测COD方法, 该组合权值模型是基于反向区间偏最小二乘法(BiPLS)结合组合区间偏最小二乘法(SiPLS)算法对紫外光谱的特征子区间筛选组合, 然后依据特征子区间的权值建立的预测模型。 首先按照一定的浓度梯度配制45份COD标准液样本, 通过实验获取标准液的紫外光谱数据; 对获取到的COD紫外光谱数据做一阶导数和S-G滤波(Savitzky-Golay)的预处理, 消除基线漂移和环境干扰噪声; 应用SPXY(Sample set partitioning based on jiont X-Y)算法将实验样本数据组划分成校正集和预测集。 然后基于BiPLS算法对全光谱区间进行波长筛选, 在BiPLS筛选过程中, 目标区间的划分数量会对建模产生较大影响, 于是对子区间划分数量进行优化, 把子区间分成15~25个, 在不同区间数下都进行偏最小二乘(PLS)建模, 通过交互验证均方根误差(RMSECV)来筛选最优子区间数, 得到区间数为18时, 模型效果最佳。 从18个波长区间筛选出了6个特征波长子区间, 入选的子区间为2, 1, 3, 11, 7和6, 对应波长为234~240, 262~268, 269~275, 290~296, 297~303和304~310 nm, 这6个特征波长区间涵盖了大量的光谱信息, 对最终预测模型的贡献度大; 接下来通过SiPLS算法对这6个初选区间进行进一步的筛选组合, 采用不同的组合数构建不同特征区间上的PLS模型, 在相同组合数下, 筛选出一个区间组合数最优的结果, 对比不同组合数下预测模型的误差与相关性, 将6个区间筛选组合为3个特征波长区间, 分别为234~240, 262~275和290~310 nm, 这三个特征区间最佳因子数分别为4, 4和3。 对传统SiPLS的特征区间组合方法进行改进, 基于权值的大小来对这3个特征区间进行线性组合, 代替过去特征区间直接组合的方法。 通过权值公式计算出这3个特征区间的权重大小分别为0.509, 0.318和0.173, 最终建立线性组合权值COD浓度预测模型。 为了验证组合权重预测模型的精度, 另外建立了全波长范围内的PLS预测模型、 单个特征波长区间的PLS预测模型、 直接组合特征波长区间的PLS模型, 并使用评价参数相关系数的平方( R2)、 预测值与真实浓度值的均方根误差(RMSEP)和预测回收率( T)来对模型评价。 验证结果表明, 相比其他预测模型, 组合权值模型相关系数的平方达到了0.999 7, 明显优于直接组合特征区间建模的0.968 0, 预测均方根误差为0.532, 比直接组合特征区间的预测模型误差降低了29.3%, 预测回收率为96.4%~103.1%, 显著地提高了预测精度。 该方法简单可行, 不会产生二次污染, 可为在线监测水体中COD浓度提供一定的技术支持。

关键词: 紫外光谱; 区间筛选组合; 区间权值; COD浓度预测模型
中图分类号:O433.4 文献标志码:A
Combination Weight COD Concentration Prediction Model Based on BiPLS and SiPLS
CHEN Ying1, DI Yuan-jian1, TANG Xin-liang2,*, CUI Xing-ning1, GAO Xin-bei1, CAO Jing-gang1, LI Shao-hua3
1. Hebei Province Key Laboratory of Test/Measurement Technology and Instrument, School of Electrical Engineering, Yanshan University, Qinhuangdao 066004, China
2. School of Information Science and Engineering, Hebei University of Science and Technology, Shijiazhuang 050018, China
3. Hebei Sailhero Environmental Protection Hi-tech Co., Ltd., Shijiazhuang 050000, China
Abstract

The excessively high concentration of organic matter in water poses a great harm, which not only causes serious environmental pollution, but also harms human health. The traditional chemical method for detecting COD(Chemical oxygen denmand, COD) in water usually takes a long time, which is not conducive to rapid quantitative detection of COD in water. In order to solve these problems, a rapid and quantitative detection of COD using a combination of UV spectroscopy and combined weight models is proposed in this paper, the prediction model is based on the backward interval partial least squares (BiPLS) and synergy interval partial least squares (SiPLS) algorithm for screening the characteristic Intervals of UV spectra, and then based on the weights of the characteristic Intervals, a combination weight concentration prediction model is established. In this paper, 45 samples of COD standard solution are experimented; The first derivative and S-G screening of COD UV spect rum date are preprocessed to eliminate baseline drift and environmental noise; The SPXY algorithm is used to divide the experimental data sets into calibration sets and prediction sets. Then, the wavelength of the whole spectral range is screened based on the BiPLS algorithm. In the process of BiPLS screening, the selection of the number of target interval division will have a great influence on the model, so the number of Interval divisions is optimized, subintervals are divided into 15 to 25, and PLS modeling is performed under different interval numbers. The optimal subinterval number is selected by cross-validating root mean square error (RMSECV). When the number of intervals is 18, the effect of the model is the best. 6 characteristic wavelengths are selected from 18 wavelengths. The selected Intervals are 2, 1, 3, 11, 7, 6, and the corresponding wavelengths are 234~240, 262~268, 269~275, 290~296, 297~303, 304~310 nm, respectively. These 6 characteristic wavelength ranges cover a large amount of spectral information and contribute greatly to the final prediction model. Then, these 6 regions are further screened and combined through the SiPLS algorithm, PLS models with different characteristic intervals are constructed using different combinations under the same combination number, the optimal results of an interval combination number are screened out, and the error and correlation of the prediction models under different combinations are compared, the 6 interval are combined into 3 characteristic wavelength intervals, which are 234~240, 262~275 and 290~310 nm respectively. The optimal factor of the optimal PLS model for these three characteristic intervals is 4, 4 and 3, respectively. The characteristic interval combination method of the traditional SiPLS is improved, and the three characteristic intervals are linearly combined based on the weight value instead of the previous direct combination of characteristic intervals. The weights of these three characteristic intervals are calculated by the weight formula as 0.509, 0.318 and 0.173 respectively. Finally, a linear combination weight COD concentration prediction model is established. In order to verify the accuracy of the combined weight prediction model, a PLS prediction model over the full wavelength range, a PLS prediction model with a single characteristic wavelength interval, and a PLS model directly combining characteristic wavelength intervals are established, and the square of the correlation coefficient of the evaluation parameter ( R2), the root mean square error of the predicted value and the true concentration value (RMSEC) as well as the Predicted recovery (T) are used to evaluate the model. Compared with other predictive models, the verification results show that the square of the correlation coefficient of the combined weight model reaches 0.999 7, which is obviously higher than the 0.968 0 of the direct combined characteristic interval model, the prediction root mean square error is 0.532, which is more than the prediction of the direct combination characteristic intervals. The model error is reduced by 29.3%, the predicted recovery rate is 96.4%~103.1%, which significantly improves the prediction accuracy. The method is simple and feasible without generating twice pollution, which can provide some technical support for on-line monitoring of COD concentration in water.

Keyword: UV spectrum; Screen and combination of intervals; Interval weight; COD concentration prediction model
引 言

随着人类对于环境资源的开发, 环境污染问题日趋突出, 大量的有机污染物流入到水体中, 导致河流、 湖泊和海洋都受到不同程度的污染[1]。 因此, 有效监测水体污染情况显得十分迫切。 化学需氧量(chemical oxygen denmand, COD)指在一定环境下, 水体中的还原性物质被氧化分解时所消耗氧化剂的量, 单位以耗氧量mg· L-1表示[2]。 化学需氧量表征水体受到有机物污染的程度[3], 因此, COD可作为有机物监测的综合指标。

目前, 测定COD的标准方法包括高锰酸钾法和重铬酸钾法[4], 但两种方法都存在操作复杂, 测定时间长, 产生污染以及实时性差的缺点。 近年来, 各国学者进行了大量研究, 以致力于寻找快速、 环保的COD检测方法, 其中以光谱法中的紫外吸收法居多。 Leardi等将紫外光谱与遗传算法引入到COD建模当中, 建模效果良好[5]; Suzuki等开发了使用紫外-可见光谱并结合人工神经网络间接测定COD浓度的预测模型, 取得了不错的预测精度[6]; Brito等将紫外光谱与偏最小二乘相结合, 对排水系统中水体的COD浓度进行检测, 并做了验证实验, 验证结果良好[7]。 赵友全等基于紫外光谱法研制了新型的COD在线监测设备, 取得了较好的监测效果[8]。

在定量分析中, 偏最小二乘法能够在自变量存在严重相关性的情况下处理光谱, 目前已在多元光谱分析方面得到了广泛应用。 更多的研究表明, 信息区间的选取可以有效减少模型维度, 提高模型的预测能力[9]。 但是在一定条件下, 每个特征区间包含的信息量是不同的, 就需要研究特征区间涵盖的信息量对模型的贡献度, 建立线性组合权值模型。

基于上述分析, 为了获得良好的预测模型, 本文采用上述分析流程(如图1)。 首先, 使用SPXY法划分校正集和预测集样本, 并对样本进行预处理; 基于反向区间偏最小二乘法(backward interval PLS, BiPLS)对有机物紫外光谱的特征信息区间进行初步筛选, 在一定均方根误差水平下, 初选多个特征区间; 然后基于组合区间偏最小二乘法(synergy interval PLS, SiPLS)对初选特征区间进行再次筛选组合, 最终获得3个区间建立组合权值COD浓度预测模型。 并与其他几种定量分析模型进行对比, 通过实验对提出的组合权值模型进行验证, 验证结果优于其他几种模型。

图1 组合权值预测模型分析流程Fig.1 Flow chart of combined weight prediction

1 原理和算法
1.1 SPXY算法

SPXY法通过计算样本间的欧式距离, 将自变量x与因变量y之间的欧式距离也考虑进去, 从而把多维空间也包含进去[10]。

SPXY法采用dxy(p, q)代替dx(p, q); 而且对dx(p, q)和dy(p, q)做了标准化计算, 使得样本在x和y空间的权值达到了一致。

1.2 BiPLS和SiPLS算法

BiPLS是iPLS的改进算法, 是一种有效的波长筛选方法。 基本原理是将整个光谱分割成k个等宽子区间, 采用留一交互验证法对余下的k-1个光谱区间建立模型, 得到各子区间交互验证均方根误差; 去除使模型预测效果最差的一个光谱子区间, 然后对剩下的子区间继续通过留一法反复建模, 直至建模预测性能最佳[11, 12]。

SiPLS也是iPLS波长选择方法的一种扩展, 其主要思路是将同一次区间划分中, 把精度高的几个局部模型所在的子区间联合起来, 以交互验证均方根误差值为联合模型衡量指标, 选出最佳联合子区间, 在最佳联合子区间的基础上建立模型。

1.3 权值算法

区间权值[13]根据公式计算

minimize‖c-∑j=1jwjRjbj‖2subject1≥wj≥0, ∑j-1jwj=1(j=1, 2, …, j)(2)

其中, wj是第j个模型权值; Rj(m× h)是第j个光谱矩阵, bj是第j个PLS模型回归系数。

最终的线性组合权值模型可表示为

YP=∑i=1jwjRjbj(3)

2 实验部分
2.1 仪器与方法

主要仪器包括U251紫外分光光度计、 德国Brand(1.5 mL)数字可调精密移液器、 美国Omega红外温度测量仪, 50 mL比色管, 邻苯二甲酸氢钾标准液, 配制1 000 mg· L-1的邻苯标准液, 用蒸馏水定容至标线, 摇匀, 分别稀释成1, 2, 3, 4, 5, 10, 20, 30, 40, 50, 100, 200, 300, 400和500 mg· L-1浓度备用。

采集1, 2, 3, …, 500 mg· L-1浓度的15份COD标准液样本的紫外吸收光谱, 如图2(a), 采集范围为190~310 nm, 分辨率为1 nm, 积分时间为3 ms, 每个样本重复测量5次, 结果取平均值。

图2 COD样本的紫外光谱
(a): 原始光谱; (b): 经一阶导数和S-G滤波处理过的光谱Fig.2 UV spectra of COD
(a): Original spectra; (b): Spectra processed by first derivative and S-G screen

从图2(a)可知, 不同浓度的COD标准液的紫外吸收谱主要集中在紫外波段, 且光谱具有两个典型特征吸收峰。 从官能团的角度来分析, 是由于羟基、 羧基和苯环官能团在200~310 nm具有很强吸光度的缘故, 其中第一个峰是羟基和羧基共同作用形成, 且随着邻苯标液浓度的升高, 羟基、 羧基官能团吸收带出现明显红移, 并最终吸收趋于饱和; 第二个峰是苯环官能团作用形成, 且随着标液浓度上升, 该官能团吸收带的吸收明显增强[14]。

2.2 光谱数据预处理

在采集光谱数据的过程中外界环境会产生一定影响, 导致特征光谱存在噪声。 采用一阶导数法[14]对原始光谱进行预处理, 一阶导数谱可以有效消除基线漂移、 旋转以及背景干扰。 但在放大信息的同时, 噪声也被放大, 为了消除噪声影响, 采用S-G滤波, 对一阶导数谱进行滤波。 图2(b)是经过一阶导数谱和S-G滤波处理过的特征光谱曲线。

3 结果与讨论
3.1 初选特征波长

利用SPXY算法将45组样本分成两组, 经过SPXY算法划分出的校正集与预测集如表1所示。

表1 SPXY划分的校正集与预测集 Table 1 Correction set and prediction set of SPXY

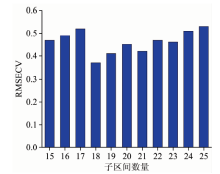
在BiPLS建模过程中, 目标区间宽度的选择会对建模产生较大影响, 因此对子区间划分数量进行优化, 这里把子区间分成15~25个, 在不同区间数下都进行PLS建模, 通过RMSECV来筛选最优子区间数。

从图3可以看出, 当选择子区间数为18时, 模型的RMSECV值最小。 基于BiPLS, 对校正集的数据进行处理, 处理结果如表2所示。

图3 不同子区间时的RMSECV值Fig.3 The RMSECV value of different intervals

表2 筛选最优区间的结果 Table 2 The result of selecting the optimal interval

表2是18个子区间的建模过程, 涵盖波长范围190~310 nm。 开始时, RMSECV随着子区间数的减少而减少, 说明过程中剔除了误差大的区间; 但后来RMSECV随着子区间数的减少逐渐增加, 表明包含信息较多的区间被剔除, 当RMSECV最小时, 认定此时所建立的PLS模型最佳。 从表2中看出, 序号6时最佳, 此时的RMSECV为0.276 2, 校正集相关系数为0.968, 主因子数为7, 入选的子区间为2, 1, 3, 11, 7和6, 对应特征波长为234~240, 262~268, 269~275, 290~296, 297~303和304~310 nm, 一共6个区间。

3.2 再次筛选特征波长区间

基于SiPLS算法对3.1节初选得到的6个特征区间再次筛选。 设置区间分割数为6, 分别采用不同的因子数构建每个特征区间上的PLS模型, 在相同组合数下, 筛选出一个区间组合最优的结果, 如表3所示。 可以看出, 随着组合数增加, 选择的区间数也在增加, 建立的SiPLS模型的交互验证误差均方根和交互验证偏差都有一定的减小, 预测相关系数也有一定的提高, 说明筛选出的特征波长区间为主要信息区间, 能够表征样品中有机物的信息。 但是当组合数为6时, 模型在预测相关系数和均方根都有一定程度的变差, 说明引入更多变量时可能会提高模型精度, 也可能会引入多余噪声降低模型的精度。

表3 不同组合数下最优SiPLS模型预测结果 Table 3 Optimal SiPLS models and prediction results under different combination numbers

从表3也能发现, 在组合数一样的情况下, 不同的区间组合得到的PLS模型的交互验证偏差、 交互验证均方根和相关系数都存在一定的差异, 这表征了每个特征波长区间所承载的光谱信息量是不同的。 因此, 在使用组合区间偏最小二乘建模过程中, 单纯的线性组合不利于模型预测精度的提高, 应考虑单个特征区间对组合模型的贡献度, 依据贡献度给每个区间赋予一定的权值, 基于特征子区间的权值, 建立线性组合权值COD浓度预测模型。

3.3 组合权值模型建立

通过观察最佳区间位置, 可以合并特征区间, 由于特征区间1, 2和3相邻, 合并为一个区间; 特征区间6和7相邻, 合并为一个区间, 最终合并相邻特征区间得到3个特征区间分别为234~240, 262~275和290~310 nm, 该特征区间最优PLS模型的最佳因子数分别为4, 4和3, 具体结果如表4所示, 通过式(2)得到这3个特征区间的权值分别为: 0.509, 0.318和0.173, 其组合权值预测模型由式(3)得到。

表4 选取特征光谱区下不同模型结果统计表 Table 4 Selection of the results of different models under the characteristic spectral region

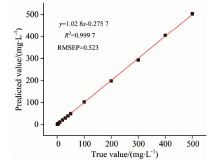
通过预测集样本对模型进行验证, 这里使用回归预测数据相关系数的平方(R2)、 预测值与真实值的预测均方根误差(RMSEP)、 预测回收率(T)对模型进行评估, 基于BiPLS和SiPLS筛选特征区间, 对筛选特征区间进行组合权值模型的回归结果如图4所示, 模型预测值与真实值之间相关系数的平方(R2)为0.999 7, RMSEP值为0.523。

图4 组合权值预测模型的回归Fig.4 Regression graph of combined weight forecasting model

基于3.2节筛选得到的特征波长区间, 分别建立模型。 其中1号模型为190~310 nm的全光谱PLS模型, 2, 3和4是基于BiPLS和SiPLS算法筛选出的特征光谱区间234~240, 262~275和290~310 nm, 分别建立的单个特征区间模型, 5号模型为选择3个特征区间直接组合后建立的模型, 6号模型是基于每个特征区间权值, 建立的组合权值预测模型。

从表4可知, 对于筛选出的单个信息区间建立的预测模型2, 3和4, 其预测精度普遍比全光谱建模1差一些, 这是因为有机物的光谱信息广泛存在该范围内, 单个特征光谱区间的信息量还是相对较少。 相比全光谱模型1, 组合模型5和6的预测相关性和均方根都有较大的提高, 预测相关性分别从0.944 1提升到0.968 0和0.999 7, 预测均方根分别从0.817下降到了0.752和0.523, 预测回收率为93.2%~110.4%和96.4%~103.1%, 预测效果提升明显。

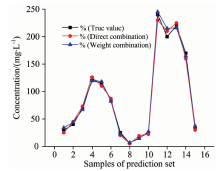
通过表4和图5, 比较模型5和6。 模型5是特征区间直接组合, 没有考虑单个特征区间涵盖信息量多少的问题; 而模型6是依据每个区间的贡献度建立的组合权值模型; 图5显示了模型5与模型6验证集样本的预测值与标准值之间的偏差情况。 可以发现, 预测精度有了进一步的提高, 相关系数的平方从0.968 0提高到了0.999 7, 预测均方根误差从0.752降低到了0.523, 比直接组合特征区间的预测模型误差降低了29.3%, 预测回收率范围从93.2%~110.4%提升到96.4%~103.1%, 预测结果图也更加贴近真实值走势。 对比上面的6组预测模型, 线性组合权值预测模型的预期效果是最好, 明显优于其他五组。

图5 直接组合与权值组合模型预测结果Fig.5 The result of combination of direct combination and weight value combination

4 结 论

提出了一种将紫外光谱与组合权值模型相结合的快速定量检测COD方法, 该组合权值模型是基于BiPLS结合SiPLS对紫外光谱的特征子区间筛选组合, 然后依据特征子区间的权值建立的预测模型, 模型中权值由特征子区间建模的贡献率计算得到。 验证实验表明: 相比其他预测模型, 组合权值模型相关系数的平方达到了0.999 7, 明显优于其他定量分析模型, 预测均方根误差为0.532, 比直接组合特征区间的预测模型误差降低了29.3%, 预测回收率为96.4%~103.1%, 远低于其他五组, 模型的适用性更好, 显著提高了预测精度。 该方法克服了传统PLS建模过程中特征区间直接组合, 没有考虑特征子区间对建模贡献度不同的问题; 且简单可行, 不会产生二次污染, 可为在线监测水体中COD浓度提供一定技术支持。

参考文献
[1] MAI Wei, ZHAO Xiao-ming, ZHANG Jian-fei, et al(买巍, 赵晓明, 张健飞, 等). Spectroscopy and Spectral Analysis(光谱学与光谱分析), 2017, 37(7): 2105. [本文引用:1]
[2] TANG Bin, ZHAO Jing-xiao, WEI Biao, et al(汤斌, 赵敬晓, 魏彪, 等). China Environmental Science(中国环境科学), 2015, 35(2): 478. [本文引用:1]
[3] Hu Yingtian, Wang X. Sensors & Actuators B Chemical, 2017, 239: 718. [本文引用:1]
[4] Lepot M, Torres A, Hofer T, et al. Water Research, 2016, 101: 519. [本文引用:1]
[5] Leardi R, Nørgaard L. Journal of Chemometrics, 2010, 18(11): 486. [本文引用:1]
[6] Suzuki Y, Kikuta Y, Yamada K, et al. Bunseki Kagaku, 2014, 63(11): 895. [本文引用:1]
[7] Brito R S, Pinheiro H M, Ferreira F, et al. Urban Water Journal, 2014, 11(4): 261. [本文引用:1]
[8] ZHAO You-quan, WANG Hui-min, LIU Zi-yu, et al(赵友全, 王慧敏, 刘子毓, 等). Chinese Journal of Scientific Instrument(仪器仪表学报), 2010, 31(9): 1927. [本文引用:1]
[9] Lepot M, Torres A, Hofer T, et al. Water Research, 2016, 101: 519. [本文引用:1]
[10] Chen Y, Luo P, Zhao Z Y, et al. Physics Letters A, 2017, 381(40): 3472. [本文引用:1]
[11] Uusheimo S, Tulonen T, Arvola L, et al. Environmental Monitoring & Assessment, 2017, 189(7): 357. [本文引用:1]
[12] Agustsson J, Akermann O, Barry D A, et al. Environmental Science Processes & Impacts, 2014, 16(8): 1897. [本文引用:1]
[13] YUAN Yong-qiang, FU Jia, CHENG Quan-guo(袁永强, 付佳, 程全国). Mathematics in Practice and Theory(数学的实践与认识), 2015, 45(16): 107. [本文引用:1]
[14] Hu Y, Wen Y, Wang X. et al. Sensors & Actuators B Chemical, 2016, 227: 393. [本文引用:2]