作者简介: 王金舵, 1989年生, 中国科学院大学博士研究生 e-mail: jinduo_aoe@163.com
腔衰荡光谱技术(CRDS)作为一种具有高灵敏度高光谱分辨率的检测方法已被广泛用于痕量气体检测。 而目前基于CRDS痕量气体检测多针对单一气体进行测量或通过多个激光器产生的多光束进行多种组分气体浓度测量。 利用DFB激光器波长可调谐特性, 通过强弱吸收峰结合, 使用单光束实现了多种温室气体的腔衰荡光谱技术同步检测。 由于大气中水汽和二氧化碳浓度较高, 为实现同一衰荡系统对三种温室气体的同步测量, 在平衡吸收损耗的基础上, 选取1 653~1 654 nm内甲烷的强吸收峰与水汽、 二氧化碳的弱吸收峰进行测量。 通过光谱叠加反演矩阵, 分别得到甲烷、 水汽、 二氧化碳的浓度。 在计算测量灵敏度过程中发现, 通过去除衰荡过程初期的部分数据点(过滤区间), 会对噪声等效吸收系数产生影响。 多数情况下, 在测量灵敏度计算方面, 列文伯格-马夸尔特算法(L-M)会优于离散傅里叶变换法(DFT); 但当衰荡曲线的单指数性下降时, 上述结论不一定成立。 搭建了一个低精细度( F≈6×103)衰荡腔对上述结论进行了实验验证。 相较于用于测量温室气体浓度的高精细度衰荡腔( F≈1×105), 低精细度衰荡腔的衰荡速率较快, 衰荡曲线的单指数性明显低于高精细度衰荡腔。 实验表明, 在过滤区间长度较短时, 采用DFT算法计算得到的噪声等效吸收系数会小于L-M算法得到的结果。 当过滤区间长度增加时, L-M算法得到的结果优于DFT算法。 在受过滤区间长度影响方面, DFT算法的波动性要明显小于L-M算法。 根据Allan方差分析, 在512次采样平均(约8 s)下的最小噪声等效吸收系数进行计算, 该CRDS装置测量灵敏度为2.4×10-10 cm-1。 在25 ℃标准大气压下, 对应甲烷、 水汽、 二氧化碳的测量灵敏度分别为0.64 ppbv, 3.5 ppmv和4.0 ppmv。 基于该CRDS装置, 通过单光束多波长测量方法, 利用光谱叠加反演矩阵, 测得大气中甲烷、 水汽、 二氧化碳浓度分别为2.018, 3 654和526 ppmv; 而采用经典CRDS单波长测量得到的甲烷、 水汽、 二氧化碳浓度分别为2.037, 3 898和630 ppmv。 通过与温控调节波长, 逐点扫描得到的光谱吸收曲线进行对比, 采用多波长测量得到气体浓度进行复合拟合的光谱曲线残差小于单波长测量得到气体浓度进行简单拟合的光谱曲线残差。
The cavity ring down spectroscopy (CRDS) has been a proper detecting method for the trace gas with its ultrahigh sensitivity and super spectral resolution. However, the common CRDS is designed for a single gas or the measurement of multiple species with several laser sources. In this paper, a CRDS instrument has been developed for multicomponent greenhouse gas synchronous detection with a single laser. Considering the balance of the absorption losses, it utilizes the strong absorption peak of methane (CH4) and weak ones of vapor (H2O) and carbon dioxide (CO2) in the range of 1 653~1 654 nm simultaneously. The wavelength scan of that range is completed by a tunable distribution feedback laser diode. The corrected concentration of greenhouse gas has been determined by the CRDS instrument with a high finesse ( F≈1×105) cavity and calculated with the spectral superposition inversion matrix. It demonstrates that the remove of data points, called the filter region, at the preliminary stage of the decay has an influence on the noise equivalent absorption coefficient, which has a interrelation with the measuring sensitivity. In most cases, the Levenberg-Marquardt (L-M) algorithm, which shows a good precision, is better than the discrete Fourier transform (DFT) algorithm on the measuring sensitivity as a fitting algorithm. But this conclusion will be dubious when the ring-down curve is deviated from the single exponential form. For studying this phenomenon, a CRDS instrument with a low finesse cavity ( F≈6×103) is set up. Compared to the high finesse cavity, the low finesse cavity has a faster decay rate, and a bigger deviation from the single exponential form, which can be easily seen from the residual analyses. When the filter region is not long enough, the noise equivalent absorption coefficients calculated by L-M algorithm is larger than the ones calculated by DFT algorithm. Meanwhile, according to the definition of the fluctuation of the noise equivalent absorption coefficient, the influence of the DFT algorithm is less than that of the L-M algorithm affected by the length of the filter region in both high finesse cavity and low finesse cavity. The best length of the filter region in our CRDS instrument is 20 data points, which are basically the same at different averaging time. And according to Allan variance, the measuring sensitivity of the CRDS instrument can reach 2.4×10-10 cm-1 for an 8 s integration time. At 25 ℃ and 1 atm, the measuring sensitivities of CH4, H2O and CO2 are approximately 0.64 ppbv, 3.5 ppmv and 4.0 ppmv separately. Calculated with the spectral superposition inversion matrix, the atmospheric concentrations of CH4, H2O and CO2 in the lab are measured to 2.018 ppmv, 3 654 ppmv, and 526 ppmv separately with multiple wavelengths, in contrast to the results of 2.037 ppmv, 3 898 ppmv and 630 ppmv in the classical CRDS method. Using the temperature control of the DFB laser, an absorption spectrum of the greenhouse gas has been acquired with the wavelength scan. Compared to this measured results, the residuals of the complex fitting curve using the data from the multiple wavelength measurements are less than the ones of the simple fitting curve with data from the classical method.
温室气体会造成温室效应, 导致全球变暖, 海平面上升等问题。 主要的温室气体包括二氧化碳(CO2)、 甲烷(CH4)、 水汽(H2O)。 根据世界气象组织(WMO)发布的大气温室气体状态报告[1], 2016年, CO2全球平均浓度达到了(403.3± 0.1) ppmv, 比工业革命前增长了45%。 同为温室气体的CH4, 全球平均浓度更是增至(1.853± 0.002) ppmv, 是工业革命前的2.57倍。 应对日趋严重的全球变暖危机, 温室气体的监控是必不可少的关键环节。 精确测量温室气体浓度, 将有助于研究人员对其浓度变化规律的掌握, 从而更好应对全球变暖问题。 最近, 关于CH4导致地球表面温室效应不断增加的论断首次得到直接证明[2]。 CH4作为具有较强的温室效应能力(CO2的23倍)的温室气体, 其大气含量远低于其他两者, 更需要具有高灵敏度的检测手段对其进行检测。
在气相原子和分子研究领域, 直接吸收光谱技术是应用最为广泛的分析技术, 缺点在于测量灵敏度较低。 研究人员通过增加有效吸收光程的方法来提高其灵敏度, 其中腔衰荡光谱技术(cavity ring-down spectroscopy, CRDS)[3]尤为突出。 CRDS拥有较高的灵敏度, 装置相对简单, 可实现自标定, 具备出色的样品选择性, 可用于多组分气体检测[4]。 近些年来, 研究人员已采用CRDS对大气中多种气体进行了精确检测, 其中包括CH4和CO2等温室气体[5, 6, 7, 8, 9]。 Romanini等[10]首次实现了连续波腔衰荡光谱技术(CW-CRDS), 并预言采用紧凑的二极管激光器(LD)为光源的CW-CRDS在痕量检测方面非常具有前景。 Morville等[11]采用分布反馈式二极管激光器(DFB-LD)实现了标准大气状况下甲烷浓度的测量, 检测限为0.2 ppmv。 Chen等[6]采用双激光器CRDS分析仪, 在对流层对CO2和CH4进行了连续航空测量, 文中提出若对水汽同时进行测量, 则无需干燥的空气样本或进行航空定标。 臧昆鹏等[7]在采用CRDS技术进行大气甲烷测量时, 通过分析甲烷与水汽含量间的关系, 对水汽影响进行校正, 有效降低了测量偏差。 但是, 若仅根据测量数据对甲烷测量中的水汽影响进行校正, 那么校正方法在普适性上会受到一定影响。
本工作通过波长扫描的方法, 考虑平衡吸收损耗, 利用甲烷附近的二氧化碳和水汽的弱吸收峰, 实现了单光束CRDS对CH4, H2O和CO2的同步检测。 通过光谱叠加反演, 得到了上述三种温室气体的校正浓度。 此外, 针对常用衰荡时间提取算法中的列文伯格-马夸尔特算法(L-M)和离散傅里叶变换法(DFT)对测量灵敏度以及过滤区间的影响进行了比较。 多数情况下, 前者在测量灵敏度方面优于后者, 但受过滤区间长度影响大于后者。
依据朗伯-比尔定律, 假设介质吸收与光强无关, 激光在充满均匀介质的谐振腔中往返, 其光强呈单指数衰减。 与其他吸收光谱技术不同, CRDS的测量对象并非衰减后的光强, 而是光强衰减到初始值的1/e的时间[12]。 定义该时间为衰荡时间τ (λ ), 表示为
式(1)中, L为有效腔长, c为光速, R为反射率, α (λ )为介质在波长λ 处的吸收系数。 当无吸收介质时, α (λ )为零, 此时衰荡时间为空腔衰荡时间, 记为τ 0。 利用衰荡时间τ (λ )和空腔衰荡时间τ 0, 结合介质在波长λ 处的吸收截面, 可以得到介质浓度。
气体吸收谱线在压力、 温度影响下会发生展宽。 在压力影响下, 吸收谱线发生碰撞展宽, 呈洛伦兹线型; 在温度影响下, 谱线发生多普勒展宽, 呈高斯线型; 同时受两者影响时, 谱线可以用Voigt线型表示, 该线型由洛伦兹线型与高斯线型卷积得到[13]。 展宽效应会导致吸收光谱发生交叠, 即波长λ 处的吸收系数α (λ )为多种分子吸收系数的叠加。 采用单一波长进行痕量气体测量, 该波长对应的吸收损耗实际为多组分气体吸收损耗的总和。 若依据经典CRDS理论, 仅根据单一吸收波长, 计算一种气体浓度, 将会导致测量浓度偏高。 而同时采用多个波长进行测量, 联立求解, 将实现多组分痕量气体测量, 并且可以对测量浓度进行校正, 使各自测量浓度更接近真实值。
基于CRDS的痕气检测的本质在于测量吸收损耗, 即吸收系数α (λ )与有效光程的乘积。 当有效光程一定时, 吸收系数越大, 则吸收损耗越大。 而较大的吸收损耗会缩短衰荡时间, 从而影响测量灵敏度。 为确保单光束多组分温室气体CRDS同步检测均具有较高的测量灵敏度, 需要平衡三种温室气体的吸收损耗。 由于吸收系数为待测气体浓度与吸收截面的乘积, 当气体浓度较高时, 需要小吸收截面; 反之, 气体浓度较低时, 需要大吸收截面。 大气中, CO2浓度为百ppmv量级, H2O浓度为千ppmv量级甚至更高, 而CH4浓度仅约为2 ppmv。 所以, 选择在单光束光源输出波长时, 在有限的波长扫描范围内, 应使CH4的吸收截面比H2O和CO2的吸收截面至少高2~3个数量级。
选取CH4吸收峰R(3)附近进行波长扫描。 该吸收峰位于2v3泛频吸收带, 由三根谱线构成, 在展宽效应作用下, 相互叠加形成连续的吸收峰, 中心波长λ 2为1 653.722 nm[14]。 利用HITRAN数据库提供的分子吸收谱线强度及相关参数, 通过Voigt线型拟合, 可以得到25 ℃标准大气压下CH4, H2O和CO2在1 653.7 nm附近的吸收截面, 如图1所示。
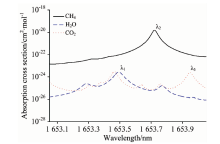 | 图1 1 653.7 nm附近CH4, H2O和CO2吸收截面Fig.1 Absorptions cross sections of CH4, H2O and CO2 at 1 653.7 nm absorption line |
从图1中可以看到, 在CH4吸收峰附近有较弱的H2O吸收峰, 中心波长λ 1为1 653.494 nm, 以及较弱的CO2吸收峰, 中心波长λ 3为1 653.948 nm。 由于1 653.466与1 653.494 nm较接近, 未采用中心波长为1 653.466 nm的CO2吸收峰进行测量以及浓度计算。
由于3种温室气体的光谱发生交叠, 在波长扫描过程中, 任意测量点必为3种气体吸收的共同作用。 在开腔CRDS装置中, 无法进行真空状态或充氮气进行空腔衰荡时间测量, 只能选取3种气体吸收均较弱(约为各气体吸收峰处吸收截面的1%)的点测得的衰荡时间为空腔衰荡时间τ 0。 吸收截面σ ij定义为i: 1表示λ 1、 2表示λ 2、 3表示λ 3; j: 1表示CH4、 2表示H2O、 3表示CO2。 假设在λ 1, λ 2和λ 3的衰荡时间分别为τ 1, τ 2和τ 3, 与τ 0的差值分别为Δ τ 1, Δ τ 2和Δ τ 3, 则计算气体浓度所需的反演矩阵可以表示为
式(2)中, N1, N2和N3分别为CH4, H2O和CO2的浓度。
在CRDS测量中, 提取衰荡时间常用的拟合算法有列文伯格-马夸尔特算法(L-M)和离散傅里叶变换法(DFT)。 L-M算法是利用指数函数y=y0+Aexp(-x/τ )进行非线性拟合, 直接得到衰荡时间。 DFT算法是在快速傅里叶变换法(FFT)的基础上发展而来的。 FFT算法是以连续数据采集为前提, 对指数函数进行傅里叶变换得到的。 而在真实的数据采集过程中, 存在采样间隔, 数据是离散的。 在这种情况下, 更适合用DFT进行衰荡时间的拟合。 上述算法的相关公式及推导可参考文献[15], 在此不做赘述。
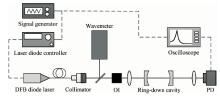
CRDS温室气体检测装置如图2所示。 采用光纤耦合输出的DFB-LD (NLK1U5FAAA, NEL)为光源, 中心波长为1 653.7 nm。 通过激光器控制器(LDC-3724C, Lightwave)温控调节, 温控调节的最小间隔为0.1 ℃, 使DFB-LD的输出波长发生规律性变化(0.12 nm· ℃-1), 用来进行波长扫描。 激光器控制器的电流设定为130 mA, 并利用信号发生器(AFG3252C, Tektronix)加载一个三角波调制信号, 调制频率为20 Hz, 幅值为50 mV。 该幅值对输出激光频率的调制略大于一个纵模间隔(750 MHz), 用于保证周期内稳定存在激光器与衰荡腔间的纵模匹配。 激光经准直器、 模式匹配镜后, 耦合进衰荡腔。 由于衰荡腔采用直线腔, 所以在光路中加入光隔离器(IO-4-1650-VLP, Thorlabs)来抑制其产生的光反馈。 衰荡腔由两片平凹高反镜组成, 在1 600~1 700 nm范围内, 正入射反射率优于0.999 9。 高反镜曲率半径为500 mm, 腔镜间隔为200 mm, 组成的衰荡腔为稳定谐振腔。 在波长扫描过程中, 通过波长计(771B-IR, Bristol)对输出激光波长进行监测, 准确度为± 1 pm, 重复精度为± 0.1 pm。 透射光经透镜聚焦后由光电探测器(PDA10CS-ES, Thorlabs)接收, 输入示波器(MSO 4104, Tektronix)。 对示波器设定触发阈值, 当透射光强达到阈值时, 通过示波器外部接口与激光控制器连接, 利用电流调控的方式实现关断, 产生衰荡信号, 由示波器记录衰荡曲线。
CRDS实验装置的测量灵敏度可以用噪声等效吸收系数α eq的最小值α min来表示[16]。
式(3)中, Nmin为对应吸收截面σ 的样品测量灵敏度, c为光速, Δ τ 为衰荡时间τ 的标准偏差。
通过激光器控制器对DFB-LD温度调节, 将输出激光波长调至非吸收位置(1 653.200 nm)。 采样频率为100 MHz, 采样长度为100 μ s, 在不同平均采样次数下, 记录衰荡曲线; 通过列文伯格-马夸尔特算法(L-M)拟合, 得到衰荡时间约为25 μ s。 对每种平均次数下的10组数据进行方差分析, 得到Allan方差图, 如图3所示。
从图3中可以看到, 当对衰荡信号进行512次平均(耗时约为8 s)时, CRDS实验装置的噪声等效吸收系数达到最小值α min=2.6× 10-10 cm-1。 在双对数坐标系中, 在未达到最佳平均次数前, Allan方差的斜率为-0.538 5, 接近-0.5, 与文献[17]中测量数据的Allan方差结论相一致。 根据式(2), 在25 ℃标准大气压下, 采用1 653.722 nm处的CH4吸收截面, 1 653.494 nm处的H2O吸收截面以及1 653.948 nm处的CO2吸收截面, 其对应的气体浓度测量灵敏度分别约为0.70 ppbv, 3.8 ppmv, 4.3 ppmv。
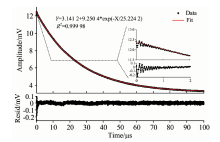
在512次衰荡过程平均下, 得到的典型衰荡曲线及单指数拟合残差如图4所示。
从图4可知, 对衰荡信号的拟合曲线呈单指数, 且具有极高的拟合度(R2=0.999 98)。 从残差图可以看出, 衰荡信号仅在衰荡初期与单指数形式有所偏离。 入射光关断时间[18]和探测器响应时间[19]的存在都可能导致衰荡曲线偏离单指数形式。 若对衰荡过程初期的部分数据点进行去除, 将可能对衰荡时间的提取精度有所帮助。 定义去除点为过滤区间, 去除点的数量为过滤区间的长度, 去除点的起始点为衰荡曲线中第一个点。
对衰荡时间的提取算法多方面研究比较[15, 20], 其中L-M算法具有较高的拟合精度, 但拟合速率较慢; 而DFT算法拟合精度相对偏低, 但具有较快的拟合速率。
在拟合速率方面, 通过Matlab软件, 对10组形如图4中的衰荡曲线进行衰荡时间提取。 L-M算法用时0.7 s, DFT算法仅用时0.006 s。 在拟合速率方面, DFT明显优于L-M算法。
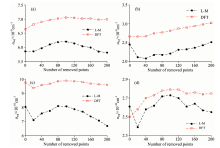
在拟合精度方面, 拟合精度可以由衰荡时间的标准偏差来表示。 由式(3)可知, 标准偏差直接影响噪声等效吸收系数, 进而影响测量灵敏度。 拟合精度越高, 测量灵敏度越高。 下面采用L-M算法和DFT算法分别对不同长度过滤区间的噪声等效吸收系数进行计算, 如图5所示。
分析表明, 过滤区间会对噪声等效吸收系数造成影响。 从图5中可以看到, 在绝大多数情况下, 不同长度的过滤区间, 经L-M算法计算得到的噪声等效吸收系数相比DFT算法均有所降低, 只是程度不同。 这表明, 在相同外界噪声影响下, 由L-M算法提取衰荡时间的精度优于DFT算法。 该结果与文献中通过模拟在衰荡信号中引入噪声的分析结果相一致。 此外, 过滤区间对两种算法提取衰荡时间的一致性方面有所不同。 利用噪声等效吸收系数α eq的最大值与最小值之差与平均值的比值来表征受过滤区间长度影响的波动程度F表示为
分别采用L-M算法和DFT算法对不同平均次数下的F进行计算, 结果如表1所示。 分析表明, 通过DFT算法提取的衰荡时间受过滤区间长度影响的程度要小于L-M算法。 去除数据点会在一定程度改变衰荡曲线的单指数程度, 而DFT算法对此的敏感性小于L-M算法。 由此推测, 相较于L-M算法, DFT算法对衰荡曲线呈单指数的要求较为宽松。 L-M算法属于非线性拟合算法, 在计算时, 需要对非线性目标函数参数的初值进行赋值, 该赋值过程直接影响计算结果。 当过滤区间长度发生变化时, 初值的赋值也将发生变化, 这种变化将可能导致拟合结果的变化。 而对于DFT算法, 过滤区间长度发生变化时, 变化的仅为参与拟合的点数, 采样间隔并未发生改变。 因此, DFT算法受过滤区间长度变化的影响较小。
| 表1 噪声等效吸收系数受过滤区间长度影响的波动性 Table 1 Fluctuation of noise equivalent absorption coefficient affected by the length of the filter region |
为验证这一结论, 采用较低反射率的腔镜搭建低精细度衰荡腔CRDS装置。 此衰荡腔精细度F约为6× 103, 低于采用高反镜搭建衰荡腔的精细度(F≈ 1× 105)。 经512次采样平均后得到衰荡曲线如图6所示。
由于低精细度衰荡腔的衰荡时间较短, 衰荡速率较快, 受光关断时间或探测器响应时间的影响较为明显[17], 衰荡曲线的单指数程度低于高精细度衰荡腔。 从图6中可以看到, 在衰荡初期存在一个明显的上升沿, 此处经单指数拟合后的残差也较大。 在不同过滤区间长度下, 分别采用L-M算法和DFT算法进行噪声等效吸收系数计算, 结果如图7所示。
 | 图7 快衰荡速率下的噪声等效吸收系数随去除点数的变化Fig.7 Noise equivalent absorption coefficient versus the number of removed points with a fast ring-down rate |
从图7中可以看到, 在去除一些数据点后, L-M算法得到的噪声等效吸收系数的最小值仍小于DFT算法得到的吸收系数, 即在测量灵敏度方面, L-M算法优于DFT算法。 但是在未去除数据点或仅去除较少的数据点(前30个)时, 在噪声等效吸收系数方面, DFT算法优于L-M, 测量精度较高。 此外, 在受过滤区间长度影响方面, DFT算法的波动性要明显小于L-M算法。 同时也表明, 在衰荡时间的提取方面, DFT算法对衰荡曲线单指数性的要求较为宽松。
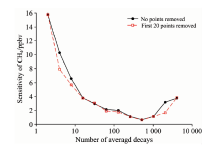
由于本工作采用高精细度衰荡腔CRDS装置进行温室气体检测, 具有较长的衰荡时间及极好的单指数性, 所以仍采用L-M算法对衰荡时间进行拟合。 为得到较高的测量灵敏度, 由图5分析可知, 应去除衰荡曲线的前20个点。 以甲烷检测为例, 通过去除衰荡曲线前20个数据点, 得到新的测量灵敏度, 如图8所示。 在不同平均次数下, 去除后的测量灵敏度均优于或等于未去除数据点的灵敏度。 采用512次平均下的噪声等效吸收系数作为最小噪声等效吸收系数进行计算, 该CRDS装置的测量灵敏度为2.4× 10-10cm-1, 对应CH4, H2O和CO2的测量灵敏度分别为0.64 ppbv, 3.5 ppmv, 4.0 ppmv。
通过DFB-LD温控调节, 对波长进行调谐, 获得多个波长下的衰荡时间, 利用光谱叠加反演矩阵, 可以计算得到实验室中大气CH4, H2O和CO2浓度。 与经典CRDS理论中, 采用单一波长进行测量, 得到衰荡时间, 进行浓度计算的结果对比如表2所示。
| 表2 多波长与单波长测量下温室气体的浓度 Table 2 The concentrations of greenhouse gas measured by multiple wavelengths and single wavelength |
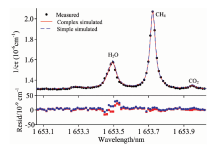
采用温控调节, 逐点进行波长扫描, 扫描步长为0.1 ℃, 测得1 653.7 nm附近温室气体光谱曲线。 基于Voigt线型, 分别采用多波长测量下的复合拟合方式与单波长测量下的简单拟合方式对光谱曲线进行拟合, 结果如图9所示。 可以看到, 拟合结果与测量结果基本一致, 仅在水汽吸收峰附近有较大残差。 两种拟合方式的残差主要在3种气体的吸收峰处有所区别, 在基线位置基本一致。 复合拟合方式残差的均方根为5.69× 10-9 cm-1, 而简单拟合方式残差的均方根为7.87× 10-9 cm-1, 大于复合拟合。
利用CRDS技术, 采用可调谐激光器, 兼顾气体强弱吸收特性, 通过反演矩阵, 实现了对3种温室气体(CH4, H2O和CO2)的同步检测。 在灵敏测量度计算过程中发现, 通过去除衰荡过程初期的数据点, 会对噪声等效吸收系数造成影响, 从而影响测量灵敏度。 分别采用L-M算法和DFT算法对点去除影响进行了分析。 结果表明, 在大多数情况下, 相比DFT算法, L-M算法提取衰荡时间的数据分布范围较小, 得到的测量灵敏度较高, 与文献结论相一致。 但当衰荡曲线的单指数性弱化时, 上述结论不一定成立, 需要去除一些数据点, 使单指数性得到改善后, L-M算法才优于DFT算法。 当过滤区间长度发生变化时, DFT算法受到的影响要小于L-M算法, 对衰荡曲线的单指数性要求较L-M算法宽松。 上述结论将有助于衰荡腔精细度较低或者衰荡时间较短的情况下数据处理及拟合算法选取。 通过去除衰荡曲线前20个数据点, 得到CRDS装置的测量灵敏度为2.4× 10-10 cm-1(8 s平均), 对应CH4, H2O和CO2的测量灵敏度分别为0.64 ppbv, 3.5 ppmv和4.0 ppmv。 在实验室环境下, 采用多波长方式, 测量大气中CH4, H2O和CO2的浓度分别为2.018 ppmv, 3 654 ppmv和526 ppmv。 分别采用多波长方式得到的浓度结果与传统的单波长方式得到的浓度结果进行光谱曲线拟合, 与波长扫描得到的实验结果进行对比。 结果表明, 利用多波长测量结果的复合拟合曲线更接近实验测量结果。 另外, 关于过滤区间长度的选取问题, 我们注意到, 结合采样频率100 MHz, 20个数据点对应的时间为200 ns, 这与我们前期通过电流调控关断激光器, 测得的光关断时间基本一致, 这一现象将作为后续的研究课题。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|