引用本文
庄新港, 刘红博, 张鹏举, 史学舜, 刘长明, 刘红元, 王恒飞. 低温辐射计黑体腔吸收率分析[J]. 光谱学与光谱分析, 2019,39(7): 2018-2022.
ZHUANG Xin-gang, LIU Hong-bo, ZHANG Peng-ju, SHI Xue-shun, LIU Chang-ming, LIU Hong-yuan, WANG Heng-fei. Absorptance Analysis of Blackbody Cavity in Cryogenic Radiometer[J]. Spectroscopy and Spectral Analysis, 2019,39(7): 2018-2022.
Doi:10.3964/j.issn.1000-0593(2019)07-2018-05  
Permissions
Copyright©2019, 《光谱学与光谱分析》期刊社
《光谱学与光谱分析》期刊社 所有
低温辐射计黑体腔吸收率分析
庄新港1,2, 刘红博1,2, 张鹏举1,2, 史学舜1,2, 刘长明1,2, 刘红元1,2, 王恒飞1,2
1. 中国电子科技集团公司第四十一研究所, 山东 青岛 266555
2. 国防科技工业光电子一级计量站, 山东 青岛 266555

作者简介: 庄新港, 1989年生, 中国电子科技集团公司第四十一研究所国防科技工业光电子一级计量站工程师 e-mail: xingangzhuang@163.com

收稿日期: 2018-05-30 接受日期: 2018-10-10
基金: 国防技术基础科研项目(JSJL2016210A001)资助
摘要

低温辐射计是目前国际上光辐射功率计量中准确度最高的测量系统, 其光辐射测量不确定度可达10-5量级, 目前国内仅有少数研究机构从国外引进低温辐射计开展计量研究, 亟待发展国产低温辐射计替代进口产品。 由于低温辐射计采用低温超导状态下的电替代测量原理进行光辐射功率测量, 发展低温辐射计的难点之一在于研制黑体吸收腔这一核心光辐射接收器件, 并要求黑体腔在各波长下的吸收率都要达到0.999 9以上。 为研制超高光谱吸收率的黑体吸收腔, 系统性分析了各影响黑体腔光谱吸收率因素, 在此基础上利用蒙特卡罗光线追迹方法重点研究了光谱波长、 腔体长度、 黑材料漫反射系数、 黑材料吸收率和入射光空间位置等对斜底黑体腔光谱吸收率的影响。 研究结果表明: 在300~1 100 nm波长范围内黑体腔吸收率与其内壁涂黑材料的吸收率呈正相关, 且在300~1 000 nm范围内的吸收率都达到了0.999 9以上, 其中在700 nm处的吸收率取得最大值0.999 941 5, 表明采用该类型黑材料的黑体腔只在300~1 000 nm范围内满足低温辐射计设计要求, 后续需要根据仿真和测试结果对低温辐射计在不同波长下的光电不等效性进行修正; 在黑体腔结构和口径确定的情况下, 黑体腔吸收率将随腔长增加而逐渐升高, 在40 mm后变化趋缓, 并在65 mm后逐渐趋于平衡, 考虑到低温辐射计低温舱对腔体尺寸的限制, 认为腔体长度与口径之比为6.5时较为合适; 黑体腔吸收率还受黑材料的漫反射系数影响, 随着黑材料漫反射系数的提高, 腔体吸收率呈现近似线性下降, 所以在选择黑体腔涂黑材料时, 在吸收率等指标相同的情况下应尽量选择镜面吸收黑; 黑材料吸收率从0.8到1的变化过程中, 腔体吸收率提升了0.05个百分点, 且黑材料吸收率为0.92时腔体吸收率可达到0.999 9以上, 表明黑材料在其有效工作波长范围内任一点的光谱吸收率都要大于0.92; 腔体吸收率还受入射光投射的空间位置影响, 光线位置越靠近斜底腔顶点处, 腔体吸收率越高, 但整体吸收率变化不明显, 光线位置对腔体吸收率影响只有不到0.004个百分点, 几乎可以忽略, 认为斜底腔不同位置处的吸收率是均匀的。 研究结果对低温辐射计黑体腔研制有一定参考价值。

关键词: 低温辐射计; 黑体腔; 吸收率; 光线追迹方法
中图分类号:O443.1 文献标志码:A
Absorptance Analysis of Blackbody Cavity in Cryogenic Radiometer
ZHUANG Xin-gang1,2, LIU Hong-bo1,2, ZHANG Peng-ju1,2, SHI Xue-shun1,2, LIU Chang-ming1,2, LIU Hong-yuan1,2, WANG Heng-fei1,2
1. The 41st Research Institute of China Electronics Technology Group, Qingdao 266555, China
2. National Opto-Electronic Primary Metrology Laboratory, Qingdao 266555, China
Abstract

Cryogenic radiometer is currently the world’s most accurate measurement system in optical radiation power metrology, and the uncertainty of measurement is up to on the order of 10 to the -5th. At present, there are only a few research institutes in the country which have imported cryogenic radiometers from abroad to carry out metrological study. A domestically-made cryogenic radiometer is urgently developed to replace imported products. Because the electrical substitution measurement principle in low-temperature superconducting state is used for optical radiation power measurements, one of the difficulties in the development of cryogenic radiometers lies in the development of a core light radiation receiving device-blackbody absorption cavity. The cavity requires a high spectral absorption over 0.999 9 at each wavelength. For the development of blackbody cavity with high absorption rate, the factors affecting the absorption rate of the blackbody cavity are given systematic analysis in this study. Based on the above, the influences of spectral wavelength, cavity length, diffuse reflectance of dark material, absorption rate of dark material and spatial position of incident light are mainly researched by Monte Carlo ray tracing method. The results showed that the absorption rate of blackbody cavity is positively associated with the absorption rate of dark material. The cavity has a high absorption rate over 0.9999 in the range of 300 nm-1000 nm, and gets the maximum value 0.999 941 5 at 700 nm. Above results indicate that the blackbody cavity meets the design requirements of cryogenic radiometer in the range of 300~1 000 nm. In the later design, the photo-electrical non-equivalent of low-temperature radiometer at different wavelengths should be corrected based on simulation and test results. If the structure and aperture are fixed, the absorption rate of blackbody cavity will gradually increase as the cavity length increases, which changes slowly at 40 mm and gradually tends to balance after 65 mm. Considering the limitation cryogenic radiometer’s cryogenic cabin, it is considered that the best ratio of the cavity length to the aperture is 6.5. The absorption rate of blackbody cavity is also affected by the diffuse reflectance of dark material. With the increase of the diffuse reflection of the black material, the absorption rate of cavity shows an approximately linear decrease. As a result, it is best to choose mirror absorption black material, when the absorption rate is the same. During the change of the absorption rate of black material from 0.8 to 1, the absorption rate of cavity increases by 0.05%. When the black material absorption rate is 0.92, the cavity absorption rate can reach over 0.999 9, which indicates that the black material should have a spectral absorbance over than 0.92 at any point within its effective operating wavelength range. The absorption rate of cavity is also influenced by the spatial position of incident light, which will get higher when the light is closer to the vertex of the inclined bottom cavity. However, the influence of light position on the absorption rate of the cavity is less than 0.004%, which is almost negligible. It is considered that the absorption rate of the inclined bottom cavity is uniform. The research results will have certain reference value for the development of cryogenic radiometer blackbody cavity.

Keyword: Cryogenic radiometer; Blackbody cavity; Absorptance; Ray tracing method
引 言

低温辐射计是目前国际上测量光辐射功率的最高基准, 其测量不确定度可达10-5量级[1, 2, 3]。 黑体腔作为低温辐射计的核心光辐射接收器件, 其根本目的是形成光陷阱, 使入射到腔体中的光辐射经过多次反射后被近似完全吸收[4]。

影响黑体腔吸收率的因素是多方面的, 除了与腔体自身结构和尺寸有关外, 还受腔体内壁涂黑材料特性、 入射光波长和空间分布情况影响。 长春光学精密机械与物理研究所Fang、 衣小龙等[5, 6]分别利用蒙特卡罗计算方法、 替代法, 仿真和测量了单一波长下黑体腔吸收率。 但到目前为止, 国内外尚未发现关于黑体腔光谱吸收率综合影响因素的报道, 而黑材料在不同波长处不同的吸收率将导致黑体腔在不同波长处的吸收率差异, 这对于低温辐射计在不同波长下的光电不等效修正具有重要意义。

本文从黑体腔的实际结构出发, 在进行单一变量控制的条件下采用蒙特卡罗(MonteCarlo)光线追迹方法对黑体腔吸收率众影响因素进行仿真分析, 给出了不同因素对腔体吸收率的影响曲线并在此基础上对各参数的选择和设置原则进行探讨。

1 斜底黑体腔吸收率特性分析

黑体腔吸收率主要取决于入射光线在腔体内部的反射次数和腔体内部涂黑材料对该波长下入射光的吸收率。 显然, 入射光在腔内反射次数越多、 黑材料吸收率越高, 腔体吸收率越高。 以圆柱腔为例, 入射光线在腔体内部的反射次数受腔体底部结构、 腔体长度与孔径比、 黑材料漫反射系数和入射光打到腔体底部的空间位置等多因素影响; 黑材料的吸收率取决于材料自身性质, 又与入射光波长相关。 在黑体腔设计过程中需要根据实际情况在各项参数之间进行权衡获取符合预期的最优解。

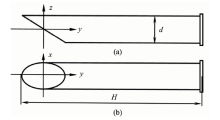
最常用的腔体形状有圆锥底圆柱腔(锥腔)和斜底圆柱腔(斜底腔)。 与锥腔相比, 斜底腔对入射光吸收率的空间均匀性好, 且便于加热器和探测器的安装, 有利于减小光电加热不等效性。 因此, 低温辐射计多采用斜底腔, 且斜底角为30° 时具有较高的吸收率[7], 如图1所示。 美国国家标准技术研究院(NIST)研制的HACR型高精度低温辐射计和英国国家物理实验室(NPL)设计CAR型低温绝对辐射计均采用斜底黑体腔[8, 9, 10]。

图1 黑体腔结构示意图
(a): 主视图; (b): 俯视图Fig.1 Schematic diagram of blackbody cavity
(a): Front view; (b): Top view

2 实验部分

腔体吸收黑材料对入射光只有吸收和反射, 其中, 反射又可以分为镜面反射和漫反射, 定义漫反射率ρd与反射率ρ 之比为黑材料的漫反射系数, 用D表示。

D=ρd/ρ

首先用SolidWorks软件完成对黑体腔的建模, 然后将黑体腔模型导入TracePro软件进行黑体腔吸收率及分布情况仿真分析。 TracePro是基于蒙特卡罗(MonteCarlo)光线追迹方法的光学分析软件, 可通过光线追迹获得不同条件下黑体腔吸收率ε 腔及其内表面辐照度分布情况。

仿真前需根据实际情况完成对光源、 涂黑材料光学特性等参数的设定。 以表1所示黑体腔和光源参数为例对黑体腔吸收率和辐照度分布情况进行仿真, 首先在黑体腔开口处设置一直径为2 mm的格点光源, 光线方向沿黑体腔轴线, 波长632.8 nm, 总光功率1 W, 追迹光线119 401条; 然后在表面属性选项中新增一新的材料表面属性, 设置吸收率=0.93, 镜面反射率与漫反射率之比为3:1, 同时利用ABg散射模型将漫反射部分光线定义为散射系数为0.25的朗伯漫反射。 考虑到在腔体内部多次反射吸收后的光线能力极低, 为进一步提高仿真精度, 将光通量门槛数设置为1× 10-6。

表1 黑体腔和光源各项参数 Table 1 The parameters of blackbody cavity and light

经光线追迹分析, 得到黑体腔内斜底面和两个侧表面的辐照度分布情况, 如图2所示。 由初始追光光线条数和到达各表面光线条数可计算出光线在黑体腔内经反射后平均到达斜底面的次数为7.2次, 到达侧表面的平均次数为6.2次。 鉴于大部分光能量在前两次反射吸收过程中基本被吸收殆尽, 为了提高辐照度分布图对比效果, 将辐照度值作对数处理。 经仿真分析, 可得到黑体腔吸收率以及黑体腔内表面辐照度分布情况, 可为黑体腔设计和后期低温辐射计光电加热不等效性修正提供参数支持。

图2 黑体腔辐照度分布色温图
(a): 斜底面; (b): 左侧面; (c): 右侧面Fig.2 Color-temperature of irradiance in blackbody cavity
(a): Sloping bottom surface; (b): Left side surface; (c): Right side surface

3 结果与讨论
3.1 入射光波长对黑体腔吸收率影响

利用单色仪和积分球测量黑体腔内壁涂黑材料在300~1 100 nm处的光谱吸收率, 整理在表2中。 黑材料光谱吸收率曲线呈现先缓慢升高再快速下降的趋势, 在700 nm处吸收率取得最大值0.942 940 8, 并在900 nm后显著下降, 在1 100 nm处的吸收率下降到0.881 910 6, 差值达到6个百分点, 如图3所示。 按表1参数构建黑体腔模型, 腔体内径设置为10 mm, 腔体长度75 mm, 根据表2依次设置黑材料在不同波长下的吸收率, 波长间隔100 nm, 漫反射系数设置为0.25。 仿真后得到黑体腔在300~1 100 nm下的光谱吸收率曲线, 整理在表2和图3中, 从图3无法辨别黑体腔在不同波长下的吸收率差异。 仔细观察表2, 可以发现黑体腔吸收率变化与黑材料吸收率变化相一致, 但整体变化幅度不明显, 其在700和1 100 nm处的吸收率差异只有不到0.01个百分点。 但值得注意的是, 该微小差异对于测量不确定度达10-5量级的低温辐射计仍然是不可忽略的。 一方面, 该黑体腔在1 000 nm以后的吸收率只有0.999, 不满足低温辐射计的设计要求; 另一方面, 在进行低温辐射计光电不等效修正时, 需要根据仿真和测试结果对低温辐射计在不同波长下的光电不等效性进行修正。

表2 黑材料和黑体腔在不同波长处的吸收率 Table 2 The absorptance of dark material and blackbody cavity in different wavelength

图3 黑体腔和黑材料光谱吸收率曲线Fig.3 The absorption curve of dark material and blackbody cavity

3.2 腔体长度对黑体腔吸收率影响

在腔体口径确定的情况下, 腔体长度越长光线在腔体内部反射次数越多, 相应的吸收率越高, 但腔体过长将对低温辐射计尺寸提出挑战, 需要在腔体吸收率和尺寸之间进行折中。 取腔体内径为10 mm, 在935 nm波长下对应黑材料吸收率0.93, 漫反射系数取0.25, 腔体长度设置范围为20~75 mm, 间隔5 mm, 追光分析后统计黑体腔吸收率与腔体长度关系, 如图4(a)所示。 可以发现腔体吸收率随腔长增加逐渐升高, 在40 mm后变化趋缓, 并在65 mm后逐渐趋于平衡, 所以腔体长度与口径之比为6.5时较为合适。

图4 不同影响因素对黑体腔吸收率的影响
(a): 腔体长度; (b): 黑材料漫反射率; (c): 黑材料吸收率; (d): 入射光空间位置Fig.4 The absorptance of blackbody cavity with different influence factors
(a): Cavity length; (b): Diffuse reflectance of dark material; (c); Absorption rate of dark material; (d): Spatial position of incident light

3.3 黑材料漫反射系数对腔体吸收率影响

同样默认腔体口径为10 mm, 长度设置为75 mm, 波长为935 nm, 黑材料吸收率设置为0.93, 黑材料漫反射系数依次设置为0~1, 间隔0.05, 追光分析后得到黑体腔吸收率随黑材料漫反射系数变化曲线, 如图4(b)所示。 随着黑材料漫反射系数的提高, 腔体吸收率呈现近似线性下降, 所以在选择黑体腔涂黑材料时, 在吸收率等指标相同的情况下应尽量选择镜面吸收黑。

3.4 黑材料吸收率对腔体吸收率影响

对黑体腔而言, 黑材料的单次吸收率越高越好, 但同时也要兼顾黑材料的镜面反射特性和低温下附着牢固性。 设置腔体口径为10 mm, 长度设置为75 mm, 黑材料漫反射系数设置0.25, 吸收率依次设置为0.8~1, 间隔0.02。 追光分析后得到黑体腔吸收率随黑材料吸收率变化曲线, 如图4(c)所示, 变化曲线可近似拟合为一条三阶线性函数, 曲线无明显拐点。 但整体而言, 黑材料吸收率对腔体吸收率影响没有想象中那么明显, 黑材料吸收率为0.8~1, 腔体吸收率只提升了0.05个百分点, 黑材料吸收率为0.92时腔体吸收率便可达到0.999 9以上。

3.5 入射光空间位置对黑体腔吸收率影响

以上分析过程中光线方向都沿黑体腔轴线, 研究中将入射光线以腔体轴线为中心进行二维扫描, 扫描面积为10 mm× 10 mm, 扫描分辨率为1 mm, 腔体口径为10 mm, 长度设置为75 mm, 波长取935 nm, 黑材料吸收率0.93, 漫反射系数0.25。 扫描完成后得到一个腔体吸收率三维效果图, 如图4(d)所示。 可以发现, 光线位置越靠近斜底腔顶点处, 腔体吸收率越高, 但总体而言吸收率变化不明显, 光线位置对腔体吸收率影响只有不到0.004个百分点, 几乎可以忽略, 认为斜底腔不同位置处的吸收率是均匀的。

4 结 论

斜底圆柱腔是当前低温辐射计采用的主流黑体吸收腔腔体结构, 通过建立斜底腔三维结构模型, 系统性分析了影响腔体吸收率的因素, 并利用蒙特卡罗光线追迹方法重点研究了影响斜底腔光谱吸收率的各关键因素及作用效果。 结果表明: (1)黑体腔吸收率与其内壁涂黑材料的吸收率呈正相关, 且在300~1 000 nm范围内的吸收率都达到了0.999 9以上, 其中在700 nm处的吸收率取得最大值0.999 941 5, 后期需要根据仿真和测试结果对低温辐射计在不同波长下的光电不等效性进行修正; (2)在腔体口径确定的情况下, 斜底倾斜角度为30° , 腔体长度与口径比为6.5时最为合适; (3)腔体内壁涂黑材料的单次吸收率越高、 镜面反射系数越高, 腔体吸收率越高, 在进行腔体内壁涂黑时应尽量选择单次吸收率优于0.92的镜面吸收黑; (4)斜底腔吸收率受入射光线空间位置轻微影响, 光线位置越靠近斜底腔顶点处, 腔体吸收率越高, 总体影响率不到0.004个百分点, 可近似认为斜底腔不同位置处的吸收率是均匀的。 另外, 入射光的角度对黑体腔的吸收率同样具有较大影响, 本研究中不再具体展开分析。 以上结论对于研制低温辐射计黑体腔结构和内壁涂黑材料的选择具有一定指导作用。

参考文献
[1] Hoyt C C, Foukal P V. Metrologia, 1991, 28(28): 163. [本文引用:1]
[2] Houston J M, Cromer C L, Hardis J E, et al. Metrologia, 1993, 30(4): 285. [本文引用:1]
[3] Liu C M, Shi X H, Chen H D, et al. Acta Optica Sinica, 2016, 45(9): 0912002-1. [本文引用:1]
[4] Fang Q Q, Fang W, Wang Y P, et al. Optical Engineering, 2012, 51(8): 086401-1. [本文引用:1]
[5] Fang Q Q, Fang W, Yang Z L, et al. Metrologia, 2012, 49(4): 572. [本文引用:1]
[6] YI Xiao-long, YANG Zhen-ling, YE Xin, et al(衣小龙, 杨振玲, 叶新, 等). Optics and Precision Engineering(光学精密工程), 2015, 23(10): 2733. [本文引用:1]
[7] Prokhorov A V, Hanssen L M. Metrologia, 2012, 41: 421. [本文引用:1]
[8] Houston J M, Rice J P. Metrologia, 2006, 43: 31. [本文引用:1]
[9] Pearson D A, Zhang Z M. Cryogenics, 1999, 39: 299. [本文引用:1]
[10] Gentile T R, Houston J M, Hardis J E, et al. Applied Optics, 1996, 3(7): 1056. [本文引用:1]