引用本文
易俐娜, 许筱, 张桂峰, 明星, 郭文记, 李少聪, 沙灵玉. 轻小型无人机高光谱影像拼接研究[J]. 光谱学与光谱分析, 2019,39(6): 1885-1891.
YI Li-na, XU Xiao, ZHANG Gui-feng, MING Xing, GUO Wen-ji, LI Shao-cong, SHA Ling-yu. Light and Small UAV Hyperspectral Image Mosaicking[J]. Spectroscopy and Spectral Analysis, 2019,39(6): 1885-1891.
Doi:10.3964/j.issn.1000-0593(2019)06-1885-07  
Permissions
Copyright©2019, 《光谱学与光谱分析》期刊社
《光谱学与光谱分析》期刊社 所有
轻小型无人机高光谱影像拼接研究
易俐娜1, 许筱1, 张桂峰2,3,*, 明星2, 郭文记2, 李少聪1, 沙灵玉1
1. 中国矿业大学(北京), 北京 100083
2. 中国科学院光电研究院, 北京 100094
3. 中国科学院大学, 北京 100049;
*通讯联系人 e-mail: russhome@126.com

作者简介: 易俐娜, 1986年生, 中国矿业大学(北京)地球科学与测绘工程学院讲师 e-mail: lina1986350@163.com

收稿日期: 2018-04-25 接受日期: 2018-09-08
基金: 国家自然科学基金项目(61405204); 中央高校基本科研业务费项目(2011QD03); 中国矿业大学(北京)大学生创新训练项目(C201802773); 中国科学院战略性先导科技专项(A类)(XDA13020506); 中国科学院科研仪器设备研制项目(YJKYYQ20170044)资助
摘要

轻小型、 低成本无人机(unmanned aerial vehicle, UAV)机载光谱成像仪的快速发展为水质监测、 精准农业提供了新的手段。 ZK-VNIR-FPG480机载高光谱成像仪是国产仪器, 拥有自主产权, 影像共有270个波段, 光谱范围为400~1 000 nm, 光谱分辨率为3 nm, 空间分辨率为0.9 m@1 km, 成像方式为运动推扫成像, 该成像仪的特点是影像之间不存在航向重叠, 只存在旁向重叠。 它在提供高光谱、 高空间分辨率影像的同时也存在着一系列问题: ①无人机的狭窄视场限制了每条航带的地面覆盖范围, 需要进行航带拼接; ②其自带的POS系统定位精度低; ③为提高作业效率, 航带间的重叠率较低, 一般设置在30%左右, 为影像拼接增加了困难; ④因飞行时受风力、 光照以及仪器自身等影响使得每条航带间存在亮度差异, 拼接时会出现拼接缝现象。 针对上述问题提出一种基于曲面样条函数和相位相关的无人机高光谱影像拼接方法, 旨在将无人机拍摄的单条高光谱航带拼接成一幅完整的带有地理坐标的全景图, 并实现影像几何和光谱上的匹配。 该方法包括以下几个步骤: 首先, 以正射影像为基准采用曲面样条函数法对高光谱航带进行地理配准, 赋予每条航带真实的地理坐标; 然后采用局部方差法计算各波段信噪比, 取分值最高的波段作为最优波段; 再利用该最优波段采用基于2幂子图像的相位相关算法来纠正航带间已经存在的地理空间映射关系, 消除航带间存在的错位; 最后选用加权平均融合法对相邻航带进行融合, 消除航带拼接时因光照、 仪器自身等影响所产生的拼接线问题, 最终得到带有绝对地理坐标的高光谱全景图。 实验使用ZK-VNIR-FPG480机载高光谱成像仪获取大理某地区的高光谱数据进行拼接, 结果表明, 该拼接方法得到的全景图拼接处没有错位现象, 几何位置准确。 选取4种典型地物拼接前后的光谱曲线, 其曲线走向基本一致, 计算拼接影像与拼接前左右影像的光谱角余弦均值为0.965 2, 光谱相关系数均值为0.863 2, 光谱信息散度均值为0.424 0, 欧式距离均值为0.494 1, 四种光谱曲线相似性测度指标客观上显示了曲线的高度相似性, 表明拼接前后同名点的光谱匹配度高, 适用于无人机高光谱数据的拼接。 该方法不仅提高了拼接影像的地理坐标精度, 还在消除拼接缝的基础上最大限度的保证了光谱的保真性, 并通过引入2幂子图像解决了影像在重叠度低的情况下配准算法失效的问题。 但拼接前相邻航带同名点间存在光谱差异, 且高光谱数据量大, 拼接耗时多, 如何利用重叠区域的像素修正系统误差, 统一拼接图像的度量空间以提升光谱精度和稳定性并提高拼接速度仍是今后需要解决的问题。

关键词: 高光谱影像; 影像拼接; 曲面样条函数法; 信噪比; 相位相关法; 加权平均融合
中图分类号:P237 文献标志码:A
Light and Small UAV Hyperspectral Image Mosaicking
YI Li-na1, XU Xiao1, ZHANG Gui-feng2,3,*, MING Xing2, GUO Wen-ji2, LI Shao-cong1, SHA Ling-yu1
1. China University of Mining & Technology, Beijing, Beijing 100083, China
2. Academy of Opto-Electronics, Chinese Academy of Sciences, Beijing 100094, China
3. University of Chinese Academy of Sciences, Beijing 100049, China
*Corresponding author
Abstract

The rapid development of small and low-cost unmanned aerial imaging spectrometer has provided new means for water quality monitoring and precision agriculture. The ZK-VNIR-FPG480 airborne hyperspectral imager is a domestic development instrument with independent property right. The image has a total of 270 bands, the spectral range is 400~1 000 nm, the spectral resolution is 3 nm, and the spatial resolution is 0.9 m@1 km. The imaging method is motion push broom imaging, which is characterized by no overlap between the images and only overlapping. While providing high spectral and high spatial resolution images, it also has a series of problems: ①the narrow field of unmanned aerial vehicle (UAV) restricts the coverage of the ground surface of each airstrip, and requires the splicing of flights; ②the positioning accuracy of its POS system is low; ③In order to improve operational efficiency, the overlap ratio between navigation bands is relatively low, which is generally set at about 30%, making it difficult to image splicing; ④Due to the influence of wind, light, and the instrument itself during flight, there is a difference in brightness between each band, and stitching occurs when stitching occurs. This paper proposes a method for splicing UAV hyperspectral images based on surface spline function and phase correlation, aiming at solving the above problems. The aim is to splice a single hyperspectral band taken by UAV into a complete panorama with geographic coordinates, and to achieve image geometry and spectral matching. The method includes the following steps: First, the hyperspectral flight is georeferenced using the surface spline function method with the orthophoto image as the reference, and the real geographic coordinates of each flight are assigned; second, the local variance method is used to calculate the signal-to-noise ratio of each band, and the highest value band is taken as the optimal band; and then the phase correlation algorithm based on the 2 power image is used to correct the existing geographic spatial mapping relations between flights and eliminate the dislocation of the flight. Finally, the weighted average fusion method is used to fuse the adjacent flights and eliminate the problem of the mosaic line caused by the illumination and the instrument itself. Through the above steps, we can get a hyperspectral panorama with absolute geographic coordinates. The experiment uses ZK-VNIR-FPG480 airborne hyperspectral imager to get the hyperspectral data of a region of Dali to splice. The results show that the splicing method has no dislocations in the panorama stitching, and the geometric position is accurate. The curve directions of the 4 typical objects before and after splicing are basically the same. The average value of the spectral cosine of the left and right images before and after the stitching image was calculated to be 0.965 2, the average value of the spectral correlation coefficient was 0.863 2, the average value of the spectral information divergence was 0.424 0, and the average value of the Euclidean distance was 0.494 1. The four kinds of spectral curve similarity measure indicators objectively showed the high similarity of the curves, indicating that the spectral matching degree of the same name point before and after splicing is high, which is suitable for the splicing of UAV hyperspectral data. The method not only improves the accuracy of the geographical coordinates of the spliced image, but also ensures the maximum spectrum fidelity on the basis of the elimination of the joint joint. The 2 power image is introduced to solve the problem of the registration algorithm failure under the low overlap of the image. However, there is a spectral difference between the same name points in adjacent bands before splicing, and the amount of hyperspectral data is large and the splicing takes more time. It is still a problem to figure out how to use the pixels of the overlapped region to correct the system error, to unify the measurement space of the image, to improve the spectral accuracy and stability and to improve the stitching speed.

Keyword: Hyperspectral image; Image mosaicking; Dcurved surface spline function; Signal to noise ratio; Phase correlation technique; Weighted average fusion
引言

随着遥感传感器的光谱分辨率不断提高, 人们对地物光谱属性、 特征的认知也不断深入, 大大加速了遥感技术的发展, 使高光谱遥感成为21世纪遥感领域重要的研究方向之一[1, 2], 它在地质、 农业、 环境、 军事、 水文、 大气等方面都有着巨大的应用前景。 目前, 绝大部分的高光谱成像仪都是搭载在卫星上的, 但是遥感卫星都是云上摄影, 对于晴天比较少, 或者小的对流云单体发生较多的特殊区域, 云层对卫星光学和红外通道成像造成的影响难以消除, 难以获得多时相、 高质量光学遥感影像。 无人机航空摄影的出现很好地弥补了上述光学遥感技术的不足。 近年来成像光谱仪硬件技术不断发展, 体积越来越小、 重量日渐减轻、 成本也逐渐降低, 将成像光谱仪与无人机集成来获取高光谱数据已成为新兴的研究领域[3]。 ZK-VNIR-FPG480是新型的机载高光谱成像仪, 它是国产化研制, 具有体积小、 质量轻、 成本低等优点, 与卫星遥感影像、 传统航空遥感影像相比, 其数据获取方式灵活, 能同时获取高空间分辨率与高光谱分辨率的影像, 但无人机图像中的狭窄视场限制了每个图像的地面覆盖范围, 需要对多张影像进行拼接, 才能有效覆盖研究区域[4]。

图像拼接是指将两幅或多幅序列图像按照其公共部分进行叠加, 得到一幅大型的具有较宽视角的无缝影像。 图像拼接主要包括图像配准和图像融合两个关键技术。 配准的目的是根据几何运动模型, 将多幅图像配准到同一个坐标系中; 融合则是将配准后的图像合成一张大的拼接图像[5]。 2003年, Barbara从算法流程方面对图像配准进行了综述。 图像配准算法流程主要包括4个步骤: 特征提取(feature detection); 特征匹配(feature matching); 确定变换模型及参数(mapping function design); 图像变换及插值(image transformation and resampling)。 其中, 空间变换模型是整个图像配准算法的基础, 影响着特征提取与匹配算法的选择。 空间变换模型可以分为两大类: 全局变换模型和局部变换模型, 全局变换模型仅用一个变换函数表示参考图像和待配准图像之间的空间变换关系; 局部变换模型将待配准图像拆分成多个区块, 对每个区块使用各自的变换函数进行单独的配准。 局部变换模型能够获得更为精确的配准结果, 但其算法复杂度高, 计算量大, 因此现有的绝大多数图像配准方法均采用全局变换模型[6]。 根据图像配准过程中利用图像信息的不同, 可将配准方法分为: 基于灰度信息的、 基于变化域的和基于局部不变性特征的, 其中基于特征的影像配准是目前最常用的方法。 对影像融合, 一般是基于像素的融合方法, 常用的有加权平均融合法、 小波变换法、 多分辨率金字塔融合法、 图切割融合法等。

目前轻小型低成本无人机遥感图像拼接存在的问题可归纳为以下3点: ①POS系统定位精度低, 导致拼接后坐标不准确; ②为提高作业效率, 航带间的重叠率较低, 一般设置在30%左右, 但目前图像配准算法都是基于50%左右的重叠度进行的, 当重叠区域较窄时常用算法会失效; ③无人机拍摄的图像因飞行时受风力、 光照以及仪器自身等的影响会不可避免的产生畸变以及亮度差异, 使得拼接时出现错位及明显拼接缝现象。

针对以上提出的3点问题, 提出一种基于曲面样条函数和相位相关的无人机高光谱数据拼接方法, 旨在将无人机拍摄的单张高光谱影像拼接成一幅完整的带有地理坐标的全景图, 并实现影像几何和光谱上的匹配。 首先以正射影像为基准采用曲面样条函数法对无人机高光谱影像进行地理配准, 然后采用局部方差法计算各波段信噪比以得到最优波段, 利用该最优波段采用基于2幂子图像的相位相关算法来纠正图像间已经存在的地理空间映射关系, 最后选用加权平均融合法对相邻影像进行融合, 得到带有绝对地理坐标的高光谱全景图。

1 算法原理

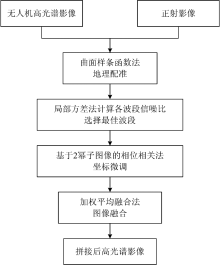
提出的拼接方法主要分为以下几大步骤: 曲面样条函数法进行地理配准、 局部方差法计算各波段信噪比、 基于2幂子图像的相位相关算法计算偏移量、 加权平均融合法进行影像融合。 技术路线图如图1所示。

图1 技术路线图Fig.1 Technology roadmap

具体步骤为:

(1)输入待拼接的高光谱影像;

(2)以正射影像为基准采用曲面样条函数法对无人机高光谱影像进行地理配准;

(3)采用局部方差法计算各波段信噪比, 选取信噪比值最高的波段作为最优波段;

(4)利用最优波段采用基于2幂子图像的相位相关算法来纠正图像间已经存在的地理空间映射关系;

(5)选用加权平均融合法对配准后的影像进行融合;

(6)输出拼接后的高光谱影像。

1.1 基于曲面样条函数法的地理配准

曲面样条函数插值方法是R.L.Harder和R.N.Desmardis于1972年创立, 就用于曲面样条函数拟合的原始数据点而言, 它们不必按规则排列, 只要提供不少于三个的任意点(控制点或采样点), 就可以得到任意阶可微的光滑曲面[7]。 当将可调控参数Cj设为0时, 校正后的图像控制点位置不发生变化, 将它应用于图像的地理配准不仅可得到较高的配准精度, 还能保证图像得到准确的拉伸, 为后续相位相关法的实现提供条件。 曲面样条函数的表达式为

w(x, y)=a0+a1x+a2y+∑i=1nFiri2ln(ri2+ε)(1)

式(1)中: a0, a1, a2, Fi(i=1, 2, …, n)为待定系数, ri2=(x-xi)2+(y-yi)2, ε 为调节曲面曲率大小的经验参数, 视实际情况适当选取。 一般地, 需要曲面减少畸变、 曲面平滑, 应使ε =1~10-2, 对于畸变较大的曲面甚至取ε =10-5~10-6。

1.2 基于局部方差法计算各波段信噪比

高光谱影像含有上百个波段, 不能对所有波段都进行相位相关法计算, 一般选择一个波段参与运算, 将得到的偏移量运用于整幅高光谱影像即可。 因此, 采用局部方差法计算各波段信噪比[8], 得到信噪比值最高的波段作为最优波段参与相位相关法的计算。 具体步骤如下:

(1)边缘提取。 基于Canny算子对图像进行边缘提取, 结果为二值图像: 边缘值为1, 非边缘值为0。

(2)边缘块剔除。 按照规定子块尺寸(4× 4)对整个图像进行分块, 统计每一个子块中是否包含有边缘值, 若有则将该子块剔除, 不再参加后面的信噪比估算。

(3)局部方差法估算噪声值。 计算每一个子块的局部标准差与均值, 在局部标准差最小值与平均值的1.2倍之间划分150个区间, 按标准差大小将各子块落入相应区间, 以此计算得到直方图。 根据直方图统计出包含子块最多的区间, 计算该区间内标准差的平均值作为噪声估计值。

(4)信噪比计算。 统计剔除边缘块后图像的像元平均值作为信号估计值, 图像信噪比的计算公式为

SNR=DN¯LSD(2)

式(2)中, SNR为图像信噪比; DN¯为图像均值; LSD为噪声估计值。

1.3 基于2幂子图像的相位相关算法计算偏移量

相位相关法, 它基于二维傅里叶变换的性质, 1975年由Kuglin和Hines提出, 具有场景无关性, 能够对纯粹二维平移的图像精确地对齐。 相位相关法的优点是算法简单、 运行速度快, 对于亮度变化不敏感, 且抗干扰能力强[9]。 由于ZK-VNIR-FPG480机载高光谱成像仪获取的航带畸变小, 航带与航带间的旋转角度和拉伸非常小, 在做过地理配准后认为航带间只存在平移关系, 由于配准误差的存在, 航带配准后依然会有微小的错位现象, 因此采用相位相关法来纠正图像间已经存在的地理空间映射关系。

设两幅离散图像f1(x, y)和f2(x, y)在空间域简单的平移相关

f2(x, y)=f1(x-dx, y-dy)(3)

则它们之间的傅里叶变换F1和F2满足式(4)

F2(ωx, ωy)=e-j(ωxdx+ωydy)F1(ωx, ωy)(4)

它们之间的共轭傅里叶变换 F1* 和 F2* 满足式(5)

F2* (ωx, ωy)=e-j(ωxdx+ωydy)F1* (ωx, ωy)(5)

这就是说, 两幅图像有相同的傅里叶变换幅度和不同的相位关系, 而相位关系是由它们之间的平移直接决定的。 两幅图像的交叉功率谱如式(6)

F1(ωx, ωy)F2* (ωx, ωy)|F1(ωx, ωy)F2* (ωx, ωy)|=e(ωxdx+ωydy)(6)

可以看出, 两幅图像的相位差等于其交叉功率谱的相位, 对其进行傅里叶变换会得到一个脉冲函数, 它在其他各处几乎为0, 只在平移的位置上不为0, 这个位置就是要确定的配准位置。

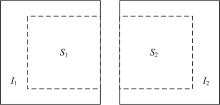
快速傅里叶算法中, 维数N必须为可以分解为一些较小整数的乘积, 当N是2的幂(即N=2p, 其中p是整数)时, 效率最高, 实现起来也最简单。 因此, 如果图像的长和宽都为2的幂, FFT计算就可以达到最高效率, 且FFT计算要求两张影像大小一致, 而航带与航带往往存在大小不一致的情况, 因此引入2幂子图像: 设图像I的宽W和高H, 则I的2幂子图像S的宽w和高h符合以下条件

w=2m≤W≤2m+1h=2n≤H≤2n+1　m, n为正整数(7)

在进行影像拼接时, 前一幅图像I1的2幂子图像S1取源图像的右边部分, 后一幅图像I2的2幂子图像S2取源图像的左边部分, 如图2所示。 则由几何关系可得, 前一幅源图像Il的2幂子图像Sl的位置

xlp=Wl-wlylp=(HL-hL)/2(8)

后一副源图像Ir的2幂子图像Sr的位置

xrp=Wr-wryrp=(Hr-hr)/2(9)

设由FFT计算出相邻图像的2幂子图像对齐时的位置偏移是(dx, dy), 则源图像间对齐偏移(Dx, Dy)=(dx+ xlp, dy+ ylp- yrp)。 利用2幂子图像可以更加快速计算出图像的偏移位置, 从而对大量的采样图像序列对齐时有着明显的速度优势, 而且不会影响最终的源图像偏移位置[10]。

图2 2幂子图像Fig.2 Two-power sub-image

1.4 基于加权平均融合法的图像融合

对重叠区的影像, 采用加权平均融合法进行图像融合。 假设I(i, j)为融合后新图像的灰度值, I1和I2为待拼接影像的图像灰度值, 则有

f(x, y)=I1(i, j)(i, j)∈I1eI1(i, j)+(1-e)I2(i, j)I2(i, j)(i, j)∈I2　(i, j)∈I1⋂I2(10)

式(10)中, e为加权系数, 设两幅影像的重叠区域在X轴方向上最大值和最小值分别为: xmax和xmin, 则加权系数e为

e=xmax-xxmax-xmin(11)

从加权系数e可以看出, 权重随着距离的变化而变化, 重叠区域的融合是一个缓慢过渡的过程, 从而消除色差的影响。 从光谱的角度考虑, 从两条航带上取值能够最大限度的保证光谱的保真性。

2 结果与讨论

实验的数据利用ZK-VNIR-FPG480机载高光谱成像仪获取, ZK-VNIR-FPG480机载高光谱成像仪是国产化研制, 拥有自主产权, 影像共有270个波段, 光谱范围为400~1 000 nm, 光谱分辨率为3 nm, 空间分辨率为0.9 m@1 km, 成像方式为运动推扫成像, 该成像仪的特点是影像之间不存在航向重叠, 只存在旁向重叠, 重叠度在30%左右, 因此在影像拼接之前先进行航带复原, 再进行航带间的拼接。 选取云南大理地区某地的两幅高光谱影像进行拼接试验。 图3是用于拼接的高光谱影像的真彩色合成图像。

图3 试验区真彩色合成图像(波段103, 63, 27)Fig.3 True color composite image in test area(band 103, 63, 27)

以该实验区域的正射影像为基准采用曲面样条函数法分别对两条航带进行地理配准, 其在UTM WGS84坐标系下显示的结果如图4所示。 可以看出经过地理配准后两条航带间依然存在错位。 运用2幂子图像的相位相关算法对配准后的图像进行坐标微调以达到精确配准, 最后进行图像融合, 拼接结果如图5所示。

图4 地理配准后高光谱影像的真彩色合成图像(波段103, 63, 27)Fig.4 True color composite image of hyperspectral image after geographical registration (band 103, 63, 27)

图5 拼接后高光谱影像的真彩色合成图像(波段103, 63, 27)Fig.5 True color composite image of hyperspectral image after stitching (band 103, 63, 27)

在地理配准部分, 经过曲面样条函数法配准后, 两条航带间仍存在错位, 说明地理配准存在误差, 造成这种误差的主要原因有两点: ①重叠区域大部分为水域, 只有小部分为建筑物和裸土, 导致在重叠区域选取的同名控制点少, 从而出现错位现象; ②配准在平差计算部分存在误差累积现象。 因此, 在实际应用中, 应尽可能多的在重叠区域寻找准确的同名控制点以提高配准精度, 为相位相关法的实现提供保障。

由于高光谱影像拼接注重光谱的保真性, 因此除了要保证几何位置正确, 还要保证拼接前后重叠区域光谱信息变化不大。 本实验提取4种典型地物(草地、 水体、 建筑物和裸土)拼接前后的光谱曲线, 如图6, 选用光谱角余弦(spectral angel cosine, SAC)、 光谱相关系数(spectral correlatin, SC)、 光谱信息散度(spectral information divergence, SID)、 欧式距离(euclidean distance, ED)指标对拼接前后的光谱曲线相似度进行评价, 其中光谱角余弦值越大相似度越大, 光谱相关系数值越大相似度越大, 光谱信息散度值越小相似度越大, 欧式距离数值越小越接近[11]。 具体计算结果见表1。

表1 拼接前后光谱曲线相似度评价 Table 1 Evaluation of similarity of spectral curves before and after splicing

图6 典型地物光谱曲线对比图Fig.6 Comparison of typical spectral curves

从图6可以看出, 两张待拼接影像的光谱差异比较大, 尤其是水体和裸土部分, 但拼接后的光谱与拼接前左、 右影像的光谱曲线整体走向比较接近。 从表1可以看出, 在光谱角余弦方面(SAC), 它的最小值为0.870 8, 最大值为0.999 5, 均值为0.965 2; 在光谱相关系数(SC)方面, 它的最小值为0.602 4, 最大值为0.995 9, 均值为0.863 2; 在光谱信息散度(SID)方面, 它的最小值为0.000 4, 最大值为1.332 4, 均值为0.424 0; 在欧氏距离(ED)方面, 它的最小值为0.001 4, 最大值为2.167 1, 均值为0.494 1。 拼接影像与待拼接左右影像光谱间存在差异主要是因为: ①往返航带的光照差异导致; ②实验区只设定了一块白板, 往返航带的辐射定标存在误差; ③两幅待拼接的影像在地里配准时进行了像素的重采样, 导致原始光谱发生了变化。

3 结论

将曲面样条函数法、 局部方差法计算各波段信噪比、 基于2幂子图像的相位相关算法、 加权平均融合法进行影像融合的图像拼接方法应用于高光谱遥感影像的拼接, 得到了带有真实地理坐标的拼接全景图, 验证了该方法在高光谱遥感影像拼接方面的可行性。 并且拼接结果几何位置准确, 光谱变化小, 拼接速度快, 为其他无人机载高光谱遥感影像的带有地理坐标的自动拼接提供借鉴。

但是, 从光谱曲线图可以看出, 拼接前相邻航带同名点间存在光谱差异, 且高光谱数据波段多, 数据量大, 拼接过程耗时多, 如何利用重叠区域的像素修正系统误差, 统一拼接图像的度量空间以提升光谱精度和稳定性并提高拼接速度仍是今后需要解决的问题。

The authors have declared that no competing interests exist.

参考文献
[1] Wang C, Guo Z, Wang S, et al. Journal of Spectroscopy, 2015, 2015: ID969185. [本文引用:1]
[2] Asadzadeh S, Roberto D S F C. International Journal of Applied Earth Observations & Geoinformation, 2016, 47: 69. [本文引用:1]
[3] XU Zhi-fang, WANG Shuang-ting, WANG Chun-yang, et al(许志方, 王双亭, 王春阳, 等). Remote Sensing Information(遥感信息), 2017, 32(1): 95. [本文引用:1]
[4] Kim J I, Kim T, Shin D, et al. International Journal of Remote Sensing, 2017, 38(8-10): 2557. [本文引用:1]
[5] CHENG Yuan-hang(程远航). Research on Aerial Remote Sensing Image Mosaic Technology for UAV(无人机航空遥感图像拼接技术研究). Beijing: Tsinghua University Press(北京: 清华大学出版社), 2016. 7. [本文引用:1]
[6] Ren X, Sun M, Zhang X, et al. Remote Sensing, 2017, 9(9): 962. [本文引用:1]
[7] GONG Sheng-sheng(龚声胜). Theoretical Research in Urban Construction(城市建设理论研究: 电子版), 2015, 5(15): 5284. [本文引用:1]
[8] ZHANG Lu, HUANG Wu-meng, ZHANG Yue, et al(张璐, 黄吴蒙, 张悦, 等). Geospatial Information(地理空间信息), 2013, 11(3): 73. [本文引用:1]
[9] ZHOU Mei-li, BAI Zong-wen, YAN Xiao-jin(周美丽, 白宗文, 延小进). Foreign Electronic Measurement Technology(国外电子测量技术), 2015, 34(5): 31. [本文引用:1]
[10] Pant M, Ray K, Sharma T K, et al. sSoft Computing: Theories and Applications, Proc. SoCTA 2016, Vol. 2 (Advances in Intelligent Systems and Computing 584). Springer, 2017. [本文引用:1]
[11] ZHANG Jun-zhe, ZHU Wen-quan, ZHENG Zhou-tao, >et al(张浚哲, 朱文泉, 郑周涛, 等). Science of Surveying and Mapping(测绘科学), 2013, 38(6): 33. [本文引用:1]