引用本文
[J]. 光谱学与光谱分析, 2019,39(3): 982-989.
Ouiem Bchir, Mohamed Maher Ben Ismail, Norah Asiri. Image Based Smoke Detection Using Source Separation[J]. Spectroscopy and Spectral Analysis, 2019,39(3): 982-989.
Doi:10.3964/j.issn.1000-0593(2019)03-0982-08  
Permissions
Copyright©2019, 《光谱学与光谱分析》期刊社
《光谱学与光谱分析》期刊社 所有
收稿日期: 2018-02-20 接受日期: 2018-06-18
Image Based Smoke Detection Using Source Separation
Ouiem Bchir, Mohamed Maher Ben Ismail, Norah Asiri
Computer Science Department, College of Computer and Information Sciences, King Saud University, Riyadh 11543, Saudi Arabia

e-mail: ouiem.bchir@gmail.com; maher.benismal@gmail.com; obchir@ksu.edu.sa

Abstract

In this paper, we propose an automatic image based smoke detection using source separation. In particular, we assume that the region of interest (smoke region) is a linear combination of smoke and background pixels, and we estimate the smoke component. More specifically, we extend the linear hyperspectral unmixing techniques to the context of image based smoke detection in order to separate the smoke component from the background. The proposed approach yields promising results especially with smoke images captured outdoor.

Keyword: Pattern recognition; Computer science; Hyperspectral
中图分类号:TN98 文献标志码:A
Introduction

Smoke alarm devices represent a safety-critical system able to save lives and properties. Typical systems use sensors which detect the decrease of the ionized molecule in the air[1]. However, such devices should be very close to the smoke source and positioned on the smoke trajectory to be effective in timely manner. Moreover, they are unable to localize the smoke source. One should notice that these limitations are more acute if the alarm system intends to detect smoke in outdoor scenes.

Image based detection through video recording of outdoor scenes emerged as a promising alternative to detect smoke. It relies on automatic detection of the smoke in video frames captured using stationary cameras. Despite the variety of image processing techniques proposed in the literature, recognizing the smoke in outdoor scene image remains a challenging task due to the complexity and high variance of the visual characteristics of the smoke in such scene[2]. Another alternative to overcome the smoke detection challenge consists in formulating it as image source separation[3]. These techniques start by modeling the background. Then, based on the assumption that the smoke region of interest is a linear combination of smoke and background, the smoke component is also modeled. Next, the feature descriptors are extracted from this smoke component. Finally, the pixels or regions are assigned to “ Smoke” or “ non-smoke” classes.

In this paper, we extend the linear hyperspectral unmixing techniques to the context of image based smoke detection in order to separate the smoke component from the background. More specifically, we apply hyperspectral linear unmixing approaches on smoke images and investigate their ability to detect the smoke component.

1 Related works

Source separation is an emerging technique in the image processing and the remote sensing field[4]. It aims to decompose a single image into several images. This decomposition gets more challenging in case of lack of knowledge about the scene being viewed which yields an infinite number of potential solutions (decompositions). Independent Component Analysis (ICA)[4] was proposed as a source separation appsoach which assumes that image components are statistically independent. ICA[4] has been used in many applications such as the discrimination between light, reflection and shadow of an object[5], the separation between artifacts in astrophysical images[6], and the categorization of reflective and fluorescent object appearance[7]. Similarly, the authors in [8-10] adopted ICA approach[4] for cartoon image decomposition into piece-wise smooth components. One should note that ICA[4] cannot be used for smoke separation because the image background in the captured scenes can be either piece-wise smooth or textural[11].

Recently, other unsupervised source separation approches have been proposed in the litterature. In particular, the authors in [12] formulated the image separation problem as a Bayesian estimation problem[13] and used the Expectation minimization EM[14] to optimize it. Similarly, the researchers in [15], proposed a source separation using the Maximum Likelihood approach, while in [16-17] the non-symmetrical half-plane (NSHP) Markov random fields and the Morphological Component Analysis (MCA) have been used respectively. On the other hand, different studies proposed the transparent layers separation[17, 18, 19] to solve the source separation challenge. Yet, the smoke pattern in the image is still considered as a texture which does not handle the transparency reflection characteristics.

The authors in [21] introduced a method to separate two transparent layers containing non-rigid scene dynamics. This method uses global-to-local space-time alignment approach to detect and align the repetitive behavior. Then, the median operator to space-time derivatives is applied to separate the two transparent layers. Besides, the researchers in [3] proposed an interactive image decomposition model which involves the user supervision through the assignment of a small number of regions to one of the image layers. Even so, the user involvement is not practical for smoke detection. In [22], the authors handled the separation of multiple image layers using spatial shifts and mixing coefficients. However, this method is restricted to uniform translations. Another research handled the separation of reflection effect captured behind glass using the particularity of the background layer and the reflection layer gradients[23]. Nevertheless, in case of smoke, this not suitable because several background scenes share similar image gradients with the smoke pattern such that the case of uniform walls and homogeneous smoke. In [11], the authors proposed a method that separates the smoke components from images using a model that mixes linearly the smoke component and the background of the image as follows

ft=atst+(1-αt)bt+nt(1)

where nt∈ RN is the model error, bt∈ RN represents the background without smoke, and st∈ RN is the smoke component. The variable α t∈ [0, 1] represents the mixing weight at a time t. More precisely, given a video frame and its corresponding background, α t is estimated by minimizing the mixing error[11]. This approach consists of three major steps: (1) The background modeling, (2) the separation of smoke component, and (3) the classification task as smoke or not. Three approaches have been proposed to define the smoke components. The first one uses the fact that neighboring smoke pixels are expected to have similar intensity. Yet, this model fails to discriminate between smoke and other objects showing surface with similar smoothness property[11]. The second approach uses the principal component analysis PCA[24]. In fact, each image block with N pixels is perceived as a point is an N-dimensional space, and pure smoke image regions are likely to lie in a low-dimensional subspace because they are similar in texture[11]. The third approach improved the PCA approach by using sparse representation to obtain all possible smoke variations. In [25], the authors compared the sparse approach to the approaches proposed in [1-2] which use wavelet[26] and LBP[27] visual descriptors, respectively. They stated that image separation based approaches in [11] outperforms the visual descriptors based approaches proposed in [1-2] whether heavy or light smoke is covering the whole or part of the image. In fact, extracting the visual feature from the smoke component only, rather than the whole image, improves the smoke detection performance.

2 Proposed approach

Typical images usually show several objects which exhibit various color and texture characteristics. The extraction of low-level features is intended to encode the visual specificities of these objects and recognize them among others. These special characteristics are typically visual signature. However, in the case of smoke images, the pixels in the region of interest can be a mixture of smoke and other background objects. In order to separate the smoke from the background, we propose to unmix the image pixels and determine the signature of each pixel called endmember or pure pixel.

Let Y=[yij] be the matrix of features where yij is the yth entry of pixel i, and let S=[skm] be the endmenber matrix where the vector sk is the signature of the element k. Let P=[pjk] be the abundance matrix where pik is the proportion of endmember k in pixel i. The convex geometry unmixing model can then be expressed as

Y=PS(2)

The problem formulation in (2) requires the unsupervised learning of both P and S. The solution to this problem is subject to:

∑i=1dpi=1(3)

and

0≤pi≤1(4)

Although the nature of a hyperspectral pixel is different from the pixel low-level feature, they are both represented using highly dimensional vectors. We propose to expand the linear hyperspectral unmixing techniques to the context of image based smoke detection and separate the smoke component from the background. Namely, we use the Mixture Analysis based on Spectral Summarization (MASS)[28], the Iterated Constrained Endmembers (ICE)[29], and Sparsity Promoting Iterated Constrained Endmember (SPICE)[30].

2.1 The Spectral Analysis Based on Spectral Summarization (MASS)

The spectral analysis based on the spectral summarization MASS[28] is based on the fuzzy clustering of the spectra of the hyperspectral image. After clustering the set of pixels Y=[yij] using FCM[31], the fuzzy memberships, U={uij}∀ i∈ 1, …, C; ∀ j∈ 1, …, N, and the C cluster centers C={C1, …, Cc} are then used to unmix the hyperspectral scene. It has been proven in [28] that the matrix of endmembers E=[ek] is defined as

E=(UUT)-1K(5)

where K=[ki]∀ i∈ 1, …, Cand kiis obtained by

ki=1∑k=1NuikmCi(6)

2.2 The Iterated Constrained Endmembers (ICE)

The Iterated Constrained Endmembers (ICE) algorithm[29] minimizes the error between the pixel and the estimated pixel while minimizing the volume bounded by the endmembers. Consequently, the algorithm detects the endmembers that offer a tight fit around the data[29]. ICE algorithm[28] minimizes the following objective function

J=(1-μ)RSSN+μSSDM(M-1)(7)

where RSS is the least squares minimization of the residual sum of squares, SSD is the sum of squared distances between endmembers SDD, and μ is the regularization parameter that balances RSS and SSD. The minimization of the objective function J is done using the quadratic programming technique.

2.3 The Sparsity Promoting Iterated Constrained Endmember (SPICE)

The Sparsity Promoting Iterated Constrained Endmember (SPICE)[30] unmixing algorithm is an extension to the ICE[29] algorithm by adding sparsity-promoting term in order to!estimate the number of endmembers. The SPICE objective function is then

J=(1-μ)RSSN+μSSDM(M-1)+SPT(8)

where SPT is the sparsity promoting term. Similarly, as for ICE[29], P is optimized using the quadratic programming of the objective function in (8).

3 Experiments
3.1 Datasets Description

In this work, we use the benchmark videos for smoke detection in [32-35]. First, we extract the frames of these videos. The obtained images are smoke free, or contain smoke with different visual characteristics. From these frames we select a subset of smoke images to build two data sets, the indoor image data set and the outdoor image data set. The indoor image data set consists of 60 000 pixels which have been collected from 6 different indoor images with different backgrounds. Figure 1 shows the considered images. As it can be seen, smoke pixels vary from solid to transparent with different texture and thickness.

Fig.1 Sample smoke images captured indoor

The outdoor image data set is another pixel wise data consisting of 110 000 pixels. 26 699 pixels are smoke pixels that vary from solid to transparent and with different texture and thickness. These pixels are taken from 11 different outdoor images with different backgrounds. Shows the considered images. Each pixel from the two data sets is labeled as smoke or smoke free pixel.

3.2 Performance Evaluation

In order to assess the performance of the proposed approach, we use the Relative Unmixing Measure[36]. This performance metric measures the unmixing performance by comparing two abundance matrices. Let P(1) be the abundance matrix obtained using the unmixing approach, and P(2) be the ground truth abundance matrix obtained using the labels of pixels in hyperspectral scene. This metric compares P(1) and P(2) and records the relativity of each pair of pixel to the same endmember. The coincidence matrices Φ (1) and Φ (2) are computed as follows

Φjl=∑i=1MPjiPli(9)

where M is the number of endmembers, j and i are the indexes of the points j and i. Then, the two coincidence matrices are used to derive the following scores

NSS(Φ(1), Φ(2))=∑j=2N∑k=1j-1Φjk(1)Φjk(2)(10)NSD(Φ(1), Φ(2))=∑j=2N∑k=1j-1Φjk(1)(1-Φjk(2))(11)NDS(Φ(1), Φ(2))=∑j=2N∑k=1j-1(1-Φjk(1))Φjk(2)(12)NDD(Φ(1), Φ(2))=∑j=2N∑k=1j-1(1-Φjk(1))(1-Φjk(2))(13)

Huber index (QHubert) can be calculated using the scores above as follows

QHubert(Φ(1), Φ(2))=N..NSS-NS.N.SN.SNS.N.DND.(14)

where N..=NSS+NSD+NDS+NDD, NS.=NSS+NSD, N.S=NSS+NDS, ND.=NDS+NDD, N.D=NSD+NDD. A large value of QHubert means that the two abundances P(1) and P(2) are highly similar.

Fig.2 Sample smoke images captured outdoor

3.3 Experimental Results

We assess the performance of the proposed approach which consists in separating smoke pixels and smoke free pixels using hyperspectral unmixing approaches on visual features as described in section 3. We first extract four visual features which are blue wavelength[37], Color Moments[26], Wavelets transform[26] and Local Binary Pattern[27] with respect to each pixel. For the color moment descriptor, we use the mean and standard deviation of a 5× 5 neighborhood of the considered pixel. The wavelet is extracted on a 10× 10 window using Daubechies low-pass filter on 5 levels. The LBP is computed using a 10x10 window, and the blue wavelength component of the pixel is used as visual descriptor. After concatenating the four considered descriptors, we obtain a 172-dimensional feature vector for each pixel. This obtained feature is then fed to the considered convex unmixing approaches which are MASS[28], ICE[29] and SPICE[30]. We assess the performance of these techniques to unmix smoke and smoke free pixels using the relative unmixing measure[36]. As explained in section 3.3, SPICE determines automatically the number of endmembers. We run it first than use the same number of endmembers for the ICE and MASS. One should mention here that the number of endmember should be the same for each image since it is related to the number of elements present in the image. One way to set this number is to run the experiment several times with respect to each approach and consider the best result. However, since SPICE determine this number in an unsupervised manner, and we need a fair comparison between the three considered approaches, we consider the value learned by SPICE.

3.3.1 Outdoor Images

We run MASS[28], ICE[29], and SPICE[30] on the 11 outdoor images and report the obtained QHubert score[36] for all images and unmixing approaches in Table 1. Notice that for all images, we use the number of endmembers learned by SPICE. As shown in Table 1, the MASS unmixing approach overtakes the other methods for all images.

Table 1 Results obtained using outdoor images

Figure 3 displays the unmixing results of the 11 outdoor images obtained using MASS[28], ICE[29], and SPICE[30]. In Figure 3, the pixels recognized as smoke are shown in white while the smoke free pixels are displayed in Black. As one can see, for image 2 the best unmxing result was obtained using MASS (0.86). In fact, for this image, although the smoke is not spread on a large area, it is thick and non transparent. Besides, the sky is blue and cloud free which yields the good unmixing performance. On the other hand, the image 11 which gave the lowest unmixing score using MASS (0.59) includes white clouds in the sky which were wrongly unmixed as smoke. The results obtained using the proposed approach to unmix smoke pixels are not satisfactory with indoor images. In fact, the similarity between the visual properties of the smoke and some regions of the indoor images, such as the light, affected the unmixing performance. On the other hand, the proposed approach yields better results with outdoor images using MASS[28] unmixing. It reached an unmixing score of 80% for some images. However, for the image which contains clouds this score decreased to 60%. Besides, the smoke was accurately detected in all indoor and outdoor images.

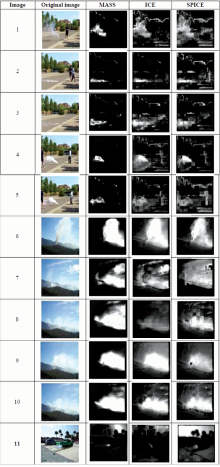Fig.3 Outdoor smoke unmixing
(a): Original image; (b): Smoke component unmixed using MASS; (c): Smoke component unmixed using ICE; (d): Smoke component unmixed using SPICE

We conducted pixel unmixing using MASS[28], ICE[29], and SPICE[30] based on the low-level features extracted from a set of indoor images. The obtained unmixing performance is reported in Table 2. As it can be seen, the QHubert unmixing score is relatively low for the three unmixing approaches with all images. This means that these approaches are unable to discriminate between smoke pixels and smoke-free pixels for indoor smoke images.

Table 2 Results obtained using indoor images

In order to illustrate these results, we display in Figure 4 a sample indoor smoke image and its corresponding smoke components obtained using MASS, ICE and SPICE, respectively. The white pixels Figure 4 (b), (c) and (d) represent the pixels unmixed as smoke while the black ones are unmixed as smoke free pixels. As one can notice, in addition to the smoke, the lights are also categorized as smoke. This inability to discriminate between smoke pixels and light pixels affects the overall performance of the unmixing approaches we use in this research, and yields the results in Table 2.

Fig.4 Example of indoor smoke detection.(a) original image, (b) smoke component unmixed using MASS, (c) smoke component unmixed using ICE, (d) smoke component unmixed using SPICE

3 Conclusions

In this paper, we proposed a novel smoke detection solution based on hyperspectral unmixing approaches. More specifically, we used unmixing approaches to recognize the image pixels which form the smoke region. The obtained results showed that for outdoor smoke images, the MASS unmixing approach[28] outperforms the other unmixing algorithms. Although the performance measure varies from one image to another, the unmxing results using MASS remain in the range [0.86, …, 0.59]. The optimal results were obtained with cases where the smoke is not spread on a large area of the image. On the other hand, the lowest unmixing results using MASS were obtained with images showing white clouds in the sky. In fact, the clouds have been wrongly unmixed and categorized as smoke pixels because they exhibit high visual similarity. The presence of lights in the images captured indoor affected the performance of the proposed unmixing based approach because the lights were wrongly detected as smoke. In order to overcome this limitation, the difference between consecutive frames can be estimated to accurately detect the smoke. This would improve the recognition of lights and/or clouds because their visual properties are exactly the same in consecutive frames, and yield better smoke detection.

Acknowledgements

This work was supported by the Research Center of the College of Computer and Information Sciences, King Saud University. The authors are grateful for this support.

The authors have declared that no competing interests exist.

参考文献
[1] Toreyin B U, Dedeoglu Y, Cetin A E. Wavelet Based Real-Time Smoke Detection in Video. in European Signal Processing Conference, 2005. 4. [本文引用:1]
[2] Tian H, Li W, Nguyen D T, et al. Smoke Detection in Videos Using Non-Redundant Local Binary Pattern-Based Features. in Multimedia Signal Processing (MMSP), 2011 IEEE 13th International Workshop on, 2011. 1. [本文引用:1]
[3] Levin A, Weiss Y. Pattern Analysis and Machine Intelligence, IEEE Transactions on, 2007, 29: 1647. [本文引用:1]
[4] Bell A J, Sejnowski T J. Blind Separation and Blind Deconvolution: an Information-Theoretic Approach. in Acoustics, Speech, and Signal Processing, 1995. ICASSP-95. , 1995 International Conference on, 1995. 3415. [本文引用:5]
[5] Farid H, Adelson E H. Separating Reflections and Lighting Using Independent Components Analysis. in Computer Vision and Pattern Recognition, 1999. IEEE Computer Society Conference on. , 1999. [本文引用:1]
[6] Funaro M, Oja E, Valpola H. Neural Networks, 2003, 16: 469. [本文引用:1]
[7] Zhang C, Sato I. Separating Reflective and Fluorescent Components of an Image. in Computer Vision and Pattern Recognition (CVPR), 2011 IEEE Conference on, 2011. 185. [本文引用:1]
[8] Meyer F G, Averbuch A Z, Coifman R R. Image Processing, IEEE Transactions on, 2002, 11: 1072. [本文引用:1]
[9] Osher S, Solé A, Vese L. Multiscale Modeling & Simulation, 2003, 1: 349. [本文引用:1]
[10] Starck J L, Elad M, Donoho D L. Image Processing, IEEE Transactions on, 2005, 14: 1570. [本文引用:1]
[11] Tian H, Li W, Wang L, et al. International Journal of Computer Vision, 2014, 106: 192. [本文引用:4]
[12] Tonazzini A, Bedini L, Salerno E. Image Processing, IEEE Transactions on, 2006, 15: 473. [本文引用:1]
[13] Sorenson H W, Alspach D L. Automatica, 1971, 7: 465. [本文引用:1]
[14] Moon T K. Signal Processing Magazine, IEEE, 1996, 13: 47. [本文引用:1]
[15] Guo L, Garland M. Pattern Recognition, 2006, 39: 1066. [本文引用:1]
[16] Guidara R, Hosseini S, Deville Y. ImageProcessing, IEEE Transactions on, 2009, 18: 2435. [本文引用:1]
[17] Fadili M J, Starck J L, Bobin J, et al. Proceedings of the IEEE, 2010, 98: 983. [本文引用:1]
[18] Szeliski R, Avidan S, Anand an P. Layer Extraction from Multiple Images Containing Reflections and Transparency. in Computer Vision and Pattern Recognition, 2000. Proceedings. IEEE Conference on, 2000. 246. [本文引用:1]
[19] Schechner Y Y, Kiryati N, Basri R. International Journal of Computer Vision, 2000, 39: 25. [本文引用:1]
[20] Levin A, Zomet A, Weiss Y. Separating Reflections from a Single Image Using Local Features. in Computer Vision and Pattern Recognition, 2004. CVPR 2004. Proceedings of the 2004 IEEE Computer Society Conference on, 2004, I-306. [本文引用:1]
[21] Sarel B, Irani M. Separating Transparent Layers of Repetitive Dynamic Behaviors. in Computer Vision, 2005. ICCV 2005. Tenth IEEE International Conference on, 2005. 26. [本文引用:1]
[22] Gai K, Shi Z, Zhang C. Blindly Separating Mixtures of Multiple Layers with Spatial Shifts. in Computer Vision and Pattern Recognition, 2008. CVPR 2008. IEEE Conference on, 2008. 1. [本文引用:1]
[23] Kong N, Tai Y W, Shin S Y. Image Processing, IEEE Transactions on, 2011, 20: 3393. [本文引用:1]
[24] Wold S, Esbensen K, Geladi P. Chemometrics and Intelligent Laboratory Systems, 1987, 2: 37. [本文引用:1]
[25] Wright J, Ma Y, Mairal J, et al. Proceedings of the IEEE, 2010, 98: 1031. [本文引用:1]
[26] Long F, Zhang H, Feng D D. Fundamentals of Content-Based Image Retrieval. in Multimedia Information Retrieval and Management, ed: Springer, 2003. 1. [本文引用:3]
[27] Pietikäinen M. Image Analysis with Local Binary Patterns. in Image Analysis, ed: Springer, 2005. 115. [本文引用:2]
[28] Bchir O, Ismail M M B, Frigui H. Mixture Analysis based on Spectral Summarization. IEEE WHISPERS Gainsville, Florida. , 2013. [本文引用:9]
[29] Berman M, Kiiveri H, Lagerstrom R, et al. IEEE transactions on Geoscience and Remote Sensing, 2004, 42: 2085. [本文引用:9]
[30] Zare A, Gader P. IEEE Geoscience and Remote Sensing Letters, 2007, 4: 446. [本文引用:6]
[31] Bezdek J C, Ehrlich R, Full W. Computers & Geosciences, 1984, 10: 191. [本文引用:1]
[32] http://www.globalmusicdepot.com/find/mp3/song/asl-vision-video-smoke-detection-demo-manufacturing-area.aspx. [本文引用:1]
[33] www.youtube.com/watch?v=WOdnleMs3Rk. [本文引用:1]
[34] https://www.youtube.com/watch?v=uSwOyGHeDkM. [本文引用:1]
[35] https://www.youtube.com/watch?v=6_j7BKioi3M. [本文引用:1]
[36] Bchir O, Ben Ismail M M. Intelligent Automation & Soft Computing, 2015. 1. [本文引用:3]
[37] Smits B. Journal of Graphics Tools, 1999, 4: 11. [本文引用:1]