试验样品为收集的烤烟样品共计150份。

美国布鲁克公司使用时间相差10年的MPA型近红外光谱检测仪两台(A, B), 美国热电尼高力公司的Antaris型近红外光谱检测仪一台(C)。 其中, 设A为主机, B和C为从机。 所有近红外光谱检测仪测量工作参数一致, 其中光谱采集方法: 积分球漫反射测量法, 采集范围: 4 00010 000 cm^-1, 分辨率: 8 cm^-1, 扫描次数: 64。

取适量烤烟烟末放入样品杯中, 取一固定重量砝码放在样品上方, 使其自然压实后进行近红外光谱扫描。

1.3.1 一阶导数与标准正态变量变换

光谱的一阶导数是NIR光谱分析中常用的基线校正和光谱分辨预处理方法。 导数光谱可有效地消除基线和其他背景的干扰, 分辨重叠峰, 提高分辨率和灵敏度。 但它同时会引入噪声, 降低信噪比^[13]。 本研究选用的是Savitzky-Golay求导法, 平滑点数为15点。

标准正态变量变换主要是用来消除因光的散射引起的光谱测量误差^[14]。 对需SNV变换的光谱X_{i, k}按式计算公式如式(1)所示

Xi, SNV=Xi, k-Xi∑k=1m(Xi, k-Xi)2(m-1)(1)

式(1)中, X_i为第i个样品光谱的平均值(标量), k=1, 2, …, m, m为波长点数; i=1, 2, …, n, n为校正集样品数。

1.3.2 不同仪器光谱偏差的评价参数与方法(残差、 一阶矩、 信噪比)

残差(residual error)是指实际观察值与估计值(拟合值)之间的差, 蕴含了有关模型基本假设的重要信息。 它应符合模型的假设条件, 且具有误差的性质。 残差的计算方法如式(2)所示

di=Xi-X'i(2)

式(2)中, X_i为第i个样品的数据估计值, X'_i为第i个样品的数据实际观察值。

离散随机信号的一阶矩(first-order moment)是随机信号的直流分量, 而造成直流分量过大的原因包括基线漂移等系统误差, 一阶矩越接近于零, 代表直流分量越接近于零, 即系统误差消除效果越好^[15]。

对于离散随机变量来说, 一阶矩的表示如式(3)所示

Mn=∑abxf(x)=1n∑1nxi(3)

式(3)中, x_i为第i个离散随机变量, n为离散随机变量的总数目。

信噪比(signal-to-noise ratio)是描述信号中有效成分与噪声成分的比例关系参数。 本实验采用最大信噪比计算方法, 即样品的最大额定信号与所有波长下的平均噪声的比值。 其计算公式如式(4)和式(5)所示

SNRi=xi, max2di2(4)di=∑j=1j=ndi, jn(5)

式(4)和式(5)中, x_{i, max}为第i个样品的额定最大信号, d_i为第i个样品在所有波长下的平均噪声, d_{i, j}为第i个样品在第j个波长点下的噪声, n为波长点数。

高斯噪声是指幅度起伏遵从高斯分布的噪声。 高斯噪声通过线性系统后, 仍是高斯噪声。 将近红外光谱仪仪器之间的差别经化学计量学方法转化为高斯分布后, 可避免进一步的线性校正。 其一维概率密度函数可用数学表达式如式(6)所示

p(x)=12πσexp-(x-a)22σ2(6)

式(6)中, a为噪声的数学期望值, 也就是均值, σ ²为噪声的方差。

本实验中, 将主机测量的光谱数据作为估计值(拟合值), 将A仪器重新装样以及在B和C两台仪器测量得到的光谱数据作为三组实际观察值, 计算残差值。 对不同仪器测得的光谱数据进行一阶导数、 SNV、 和两种方法结合的处理, 并计算残差值的一阶矩。 其中主机重新装样测量的残差值作为标准对比。 将主机的光谱数据中的最大值作为额定最大信号, 将两台从机与主机的光谱数据的残差值作为噪声成分。

1.3.3 不同仪器间模型通用性的验证与评价方法

本实验采用偏最小二乘法作为建模方法, 评价模型通用性的参数为决定系数(R²)和预测标准偏差(square error of prediction, SEP)^[2]。

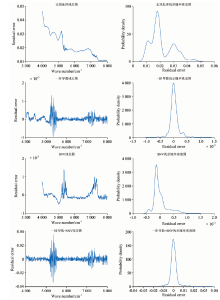
选取150份烤烟样品其中的1份, 绘出的在不同处理情况下不同厂家近红外光谱仪所测光谱数据之间的残差分布图和残差概率密度图, 具体情况如图1所示。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 不同处理情况下的残差图和概率密度图Fig.1 The residual error and it’ s probability density with different process

由图1的结果可以看出未处理的残差与原始光谱分布接近, 仍含有基线漂移和其他的背景干扰, 包含了较大的系统误差, 概率密度分布含有多个峰值; SNV处理后有所改善, 但噪声幅度变化较大, 概率密度分布峰值减少至两个; 经过导数和两种方法结合处理后的残差分布接近随机噪声, 同时概率密度分布为高斯分布。

选取150份烤烟样品其中的10份, 计算在不同处理情况下的残差一阶矩和信噪比, 并计算平均值, (其中, A-A表示主机重新装样测量, A-B表示相同厂家仪器, A-C表示不同厂家仪器)。 其中, 不同处理情况下的残差一阶矩见表1(a), 不同处理情况下的最大信噪比见表1(b)。

表1(a)

Table 1(a)

表1(a)(Table 1(a))

表1(a) 不同处理情况下的残差一阶矩 Table 1(a) First-order moment of residual error with different process 处理方法 A-A A-B A-C 无处理 -4.723× 10-3 1.453× 10-2 3.696× 10-2 一阶导数 -5.029× 10-6 3.881× 10-5 3.393× 10-5 SNV -3.566× 10-9 -1.156× 10-9 -1.927× 10-10 一阶导+SNV 5.685× 10-9 2.794× 10-9 4.817× 10-10

表1(a) 不同处理情况下的残差一阶矩 Table 1(a) First-order moment of residual error with different process

表1(b)

Table 1(b)

表1(b)(Table 1(b))

表1(b) 不同处理情况下的最大信噪比 Table 1(b) Maximal signal to noise ratio with different process 处理方法 A-A A-B A-C 无处理 195.8 43.63 17.92 一阶导数 62.67 51.43 47.70 SNV 189.7 382.7 257.9 一阶导数+SNV 59.69 70.62 60.52

表1(b) 不同处理情况下的最大信噪比 Table 1(b) Maximal signal to noise ratio with different process

由表1的结果可以看出, 无处理情况下残差一阶矩量级为10^-2~10^-3, 不同厂家仪器间差距较大; 同台仪器重新装样的最大信噪比远远大于不同台仪器, 同厂家仪器的最大信噪比是不同厂家型号仪器的两倍左右。 一阶导数处理后残差一阶矩数量级为10^-5~10^-6; 信噪比虽然数量级差距减小, 但相同仪器的最大信噪比仍高于不同仪器; SNV处理后残差一阶矩数量级为10^-8~10^-10; 不同仪器的最大信噪比远高于同台仪器, 同时信噪比值得到大幅度提升。 一阶导数与SNV结合处理后残差一阶矩数量级为10^-8~10^-9; 不同仪器的信噪比与相同仪器的信噪比基本持平, 并相比于未处理和导数有所提高。 说明导数和SNV对消除随机信号的直流分量, 减小系统偏差有着明显的效果, 其中单独使用SNV和同时使用两种方法的情况效果更好, 消除效果与同台仪器重新装样效果持平。

建模检验比例为1∶ 1, 在150个烟草粉末实验样品中, 选取75个作为建模集, 其他75个作为检验集, 对实验样品的总糖含量进行建模预测, (其中总糖含量的测定方法是流动分析法), 得到预测决定系数(R²)和预测标准偏差(SEP)结果见表2。

表2

Table 2

表2(Table 2)

表2 总糖模型预测决定系数及标准偏差(R2/SEP) Table 2 Decision coefficient and standard deviation of total sugarmodel 建模 检验 无处理 一阶导数 SNV 一阶导数+SNV A A 93.84/1.24 93.62/1.26 94.03/1.22 95.37/1.07 A B 89.41/1.62 92.72/1.35 94.23/1.20 95.30/1.08 A C 85.21/1.92 90.57/1.53 95.63/1.04 96.15/0.98

表2 总糖模型预测决定系数及标准偏差(R2/SEP) Table 2 Decision coefficient and standard deviation of total sugarmodel

由表2的结果可以看出无处理情况下, 不同仪器间的模型传递效果不理想, 其中相同厂家的不同仪器预测决定系数下降约4%, 不同厂家仪器预测决定系数相差8%, 且标准偏差相差较大。 分别进行一阶导数和SNV处理后, 预测决定系数有显著提高, 预测标准偏差差别缩小。 其中, 一阶导数处理后不同厂家仪器之间仍相差3个百分点, 标准偏差差别有所减小。 SNV处理后不同厂家仪器决定系数差别为1%, 标准偏差的差别进一步减小。 而一阶导数与SNV结合处理后, 效果优于任一方法单独处理, 预测决定系数相差在一个百分点以内, 同时R²均在95%以上, 标准偏差值均维持在1左右, 可以看出, 在处理后R² 显著提高, 标准偏差值显著降低, 同时不同仪器间差值在0.1以内, 相比于单独处理有明显减小。