引用本文
余克强, 赵艳茹, 何勇. 运用响应面分析法优化激光诱导土壤等离子体测试参数[J]. 光谱学与光谱分析, 2019,39(2): 577-583.
YU Ke-qiang, ZHAO Yan-ru, HE Yong. Application of Response Surface Methodology for Optimizing Test Parameters of Laser-Induced Plasma in Soil[J]. Spectroscopy and Spectral Analysis, 2019,39(2): 577-583.
Doi:10.3964/j.issn.1000-0593(2019)02-0577-07  
Permissions
Copyright©2019, 《光谱学与光谱分析》期刊社
《光谱学与光谱分析》期刊社 所有
运用响应面分析法优化激光诱导土壤等离子体测试参数
余克强1,2, 赵艳茹3, 何勇3,*
1. 西北农林科技大学机械与电子工程学院, 陕西 杨凌 712100
2. 农业农村部农业物联网重点实验室, 陕西 杨凌 712100
3. 浙江大学生物系统工程与食品科学学院, 浙江 杭州 310058
*通讯联系人 E-mail: yhe@zju.edu.cn

作者简介: 余克强, 1986年生, 西北农林科技大学机械与电子工程学院讲师 E-mail: yuke406336022@163.com

收稿日期: 2017-11-15 接受日期: 2018-04-02
基金: 国家自然科学基金项目(61705188), 陕西省自然科学基础研究计划项目(2017JQ3008)和中国博士后科学基金项目(2017M613218)资助
摘要

测试参数的选择和优化是进行激光诱导击穿光谱(LIBS)试验的重要步骤之一,合适的测试参数能够保障所得光谱数据的准确性。 本研究运用LIBS技术,以土壤中主要元素(硅、 铁、 镁、 钙、 铝、 钠、 钾等)为载体,研究LIBS不同测试参数对元素谱线特性影响, 优化得到普适的土壤测试条件。 设计了以LIBS系统中激光脉冲能量(LE)、 延迟时间(DT)和聚焦透镜到样品的距离(LTSD)三因素的二次中心组合的试验, 以土壤中主要元素的特征谱线组合信背比(SBR) YSBR为目标函数, 分析了三因素之间交互作用对 YSBR的影响。 结果表明: 因素DT对 YSBR的线性效果显著, 而LE和LTSD对 YSBR的线性效果均不显著; 三者的交互影响对 YSBR的交互效果都不显著; 对于二次项LE2, DT2和LTSD2对 YSBR的曲面效应均显著。 优化得到最佳的试验条件是: 激光能量LE为103.09 mJ, 延迟时间为2.92 μs, 透镜到样品的距离LTSD为97.69 mm, 得到最大组合信背比 YSBR为198.602。 这些测试参数是后期LIBS数据准确分析的前提, 为田间实地土壤LIBS检测参数的选择提供重要的借鉴。

关键词: 激光诱导击穿光谱; 测试参数; 响应面; 信背比
中图分类号:TN249 文献标志码:A
Application of Response Surface Methodology for Optimizing Test Parameters of Laser-Induced Plasma in Soil
YU Ke-qiang1,2, ZHAO Yan-ru3, HE Yong3,*
1. College of Mechanical and Electronic Engineering, Northwest A&F University, Yangling 712100, China;
2. Key Laboratory of Agricultural Internet of Things, Ministry of Agriculture and Rural Affairs, Yangling 712100, China
3. College of Biosystems Engineering and Food Science, Zhejiang University, Hangzhou 310058, China
Abstract

The selection and optimization of the test parameters is one of the important steps in spectrochemical analysis based on laser-induced breakdown spectroscopy(LIBS). Appropriate test parameters can guarantee the accuracy of the later spectral data analysis. Here,LIBS technology was employed to study the influence of different test parameters of LIBS on the spectral characteristics of main elements in soils,and the universal soil testing parameters were obtained. Based on single variable test,the experiment of laser energy (LE), delay time (DT),and lens to sample distance (LTSD) three factors quadratic central composite design was carried out using the respond surface method (RSM). According to the mainelements(Si,Fe,Mg, Ca, Al, Na, K, etc.) in soil, the combined signal-background-ratio (SBR) of characteristic spectral lines from main elements was named as the objective function ( YSBR). The interaction influences among three factors on soil plasma characteristics were explored and the optimized parameters of LIBS were summarized. Results revealed as follows: the factor LE showed a remarkable linear effect to YSBR, and factors of DT and LTSD exhibited an opposite result. The interaction of three factors displayed a non-significant relationship. Meanwhile, the quadratic terms of LE2, DT2 and LTSD2 had a significant surface relationship. Through the RSM analysis, the optimized experimental parameters were: LE: 103.09 mJ; DT: 2.92 μs; LTSD: 97.69 mm; and a peak value YSBR of 198.602 could be obtained. These optimized test parameters are the prerequisite for the LIBS data analysis in the late stage, which can offer important reference value for the soil LIBS detection in the field.

Keyword: Laser-induced breakdown spectroscopy; Test parameters; Response surface methodology; Signal-background-ratio
引 言

激光诱导击穿光谱(laser-induced breakdown spectroscopy, LIBS)是一种绿色高效的化学元素分析手段, 近些年来在工业处理、 环境监测、 考古调查、 地质勘探、 宇航探测、 农业和食品分析等[1, 2, 3]领域得到广泛的应用。 在LIBS的数据获取过程中, 激光脉冲与待测物质的相互作用产生等离子体光谱, 这是一个瞬时复杂的过程。 等离子体的特性很大程度上受到LIBS系统参数(脉冲能量、 脉冲频率、 脉冲宽度、 延迟时间、 积分时间、 数据采集方式、 样品与聚焦透镜的距离、 LIBS信号接收器的角度等)、 被测样品性状参数(以土壤为例: 水分含量、 颗粒大小、 紧实度等)、 环境气体(气体类型、 压强等)等影响[1, 2, 3, 4, 5]。 因此, 选择和优化普适性的LIBS测试条件是后期数据分析准确可靠的关键。

Tognoni等[6]研究了LIBS系统参数(激光器参数、 环境气体、 观测时间、 装置结构位置等因素)对等离子体特性的影响规律, 得到较优的测试参数。 Unnikrishnan等[7]研究了塑料物的LIBS信号在不同激光功率、 积分时间和延时时间的谱线信噪比, 得到优化的试验参数, 完成对塑料的准确分类。 张树玮等[8]研究了离焦量(透镜到样品距离)和激光能量对铝样品等离子体光谱的影响, 发现当离焦量和激光能量发生变化时, 铝元素等离子体发射谱线特性(位置、 相对峰值和半高全宽)发生明显变化。 Nicolodelli等[9]研究了LIBS区分土壤类型时激光波长, 延时时间和共线双脉冲间隔时间等参数的影响。 孙兰香等[10]运用LIBS技术分析标准高合金钢样品时, 构建了四个LIBS系统参数(激光能量、 延迟时间、 离焦量、 积分时间)对合金钢样品中铁、 铬、 锰等多种元素信背比影响的多因素模型, 并分析了LIBS系统参数对信背比的作用。 在待测物性状参数分析方面, Kim等[11]分析了土壤基体(水分和颗粒尺寸)对LIBS谱线的影响, 发现含水率增大谱线强度降低; 土壤颗粒越小, 谱线强度越高。 de Carvalho等[12]探索了植物材料粉末颗粒大小对LIBS检测结果的影响, 表明颗粒越小, 检测精度越高。 Gomes等[13]研究经过冷冻研磨和球磨研磨后的甘蔗, 橙树和大豆叶片样品的质地、 粒径和颗粒间隙各参数对LIBS信号强度和重复性的影响规律。 Fedotova等[14]比较了加入不同浓度分散剂的超纯水和纳米粒子悬浮液在LIBS检测中激光能量变化引起的曲线变化趋势。

综上所述, 现有多数研究是基于单个参数(LIBS系统参数或待测物形状参数)分析待测物激光诱导等离子体光谱特性, 进而选择和优化测试参数条件。 然而仅通过单因素分析是不够的, 应当考虑多测试参数之间交互作用对待测物等离子体光谱的特性影响。 本研究以土壤为研究载体, 以LIBS技术为手段, 运用多因素响应面分析法, 分析多测试参数交互作用对土壤等离子体谱线特性的影响规律, 优化得到土壤中多元素检测普适的LIBS测试条件。

1 实验部分
1.1 土壤样品

试验所用的土壤采自浙江大学紫金港校区试验田。 结合中国标准物质网土壤样品采集方法, 经过去除杂质(石子、 杂草和植物根系等)、 自然风干、 压碎、 研磨、 过筛、 压片等步骤, 为了得到均匀的激光烧蚀表面[15], 将土壤样品粉末制成压片, 以备后续使用。 设置台式粉末压片机(FY-24, SCJS Co. Ltd., Tianjin)的压强为10 MPa, 连续压4 min, 将3 g土壤样品粉末压成厚度约为3 mm, 直径为25 mm圆饼状土壤压片。

1.2 LIBS试验装置

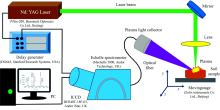
试验装置的结构示意图如图1所示, 主要的硬件结构有: 调Q的纳秒级激光器, 脉冲延时发生器, 反射镜, 焦距透镜, X-Y-Z移动平台, 中阶梯光栅光谱仪与耦合的ICCD探测器, 等离子体光谱收集器, 光纤, 计算机, 连接线等。

图1 LIBS试验装置结构示意图Fig.1 The schematic diagram of LIBS experiment setup

1.3 LIBS数据的获取

在正常空气环境气压下, 调Q的纳秒级Nd: YAG激光器频率为1 Hz, 波长532 nm, 脉冲宽度8 ns的激光脉冲光束经反射镜反射后, 由透镜(焦距f=100 mm)聚焦到土壤样品上, 瞬时烧蚀土壤样品, 产生激光诱导等离子体, 等离子体光谱由收集器汇集于光纤中并传输至中阶梯光栅光谱仪进行分光, 耦合的ICCD探测器进行光电转换, 计算机实现信号接收和显示。 数据分析和处理, 数据的采集和显示是由该光谱仪配套Solis软件(V4.25, Andor Technology, UK)来完成。

在LIBS光谱采集过程中, 激光能量(laser energy, LE)、 聚焦透镜到土壤样本的距离(lens to sample distance, LTSD)和延时时间(delay time, DT)是三个最重要的参数。 LE可由激光器自身设置, 并由激光能量计测试取值; LTSD是通过调节移动平台在Z轴方向运动来实现; DT的取值通过脉冲延时发生器(Delay generator DG645)来设置的。 另外, ICCD探测器的曝光时间和门宽分别设置为0.01 s和2 μ s。 为了减少土壤样品不均匀性和激光脉冲能量波动对谱线特性的影响, 将不同位置的20次激光烧蚀的平均值作为单个LIBS光谱采样值。

1.4 试验设计与分析方法

响应面分析法(response surface methodology, RSM)是一个用于设计试验, 建立模型, 评估因素影响和寻找最佳条件的统计技术的集合[16, 17, 18]。 该方法可以以最少的试验数量达到优化试验结果的目的, 而无需研究所有可能的组合试验。 它可以量化单个或多个测量响应与重要输入因素之间的关系, 并以回归分析精确地表述因素和响应值之间的回归关系式[16, 17, 18]。 通常, 对于一个二阶的多元回归分析, 可以得到以下二次多项式模型(1)

Y=B0+∑i=1kBiXi+∑i=1kBiiXi2+∑i=1k-1∑j=2kBijXiXj(1)

其中: Y是试验的响应值, X是试验因素变量的取值, B0是常数项, Bi是一次线性系数, Bii是二次曲面系数项, Bij是因素的交互作用系数, k是试验因素的个数。 本研究中响应面的试验设计和后续分析是利用Design-Expert软件(Version 8.05b, Stat-Ease, Inc. USA)完成的。

2 结果与讨论
2.1 试验设计结果

经前期预试验, 试验设计为, 激光脉冲能量: 50 mJ≤ LE≤ 160 mJ; 检测器相对与激光脉冲的延迟时间: 0.5 μ s≤ DT≤ 4.5 μ s; 聚焦透镜到土壤样品表面的距离: 94 mm≤ LTSD≤ 102 mm(由于透镜焦距f=100 mm, 烧蚀表面位于透镜聚焦点上方时LSTD小于100 mm, 烧蚀表面位于透镜聚焦点下方LTSD大于100 mm)。

在试验设计中, 根据文献[19]中试验设计要求和参数选择, 得到本研究的三因素的二次回归中心组合的试验设计, 如表1所示。

表1 三因素二水平中心组合的试验设计结果 Table 1 The experimental results of three factors quadratic central composite design
2.2 目标函数

评价LIBS光谱数据的性能的指标一般常用对应谱线的信背比。 在实际的LIBS数据分析时, 往往是多元素同步分析, 而不同的元素谱线获取的信背比不同, 其最佳的测试条件也不同。 也就是说, 当某元素的某条谱线信背比最大时, 其他元素谱线的信背比不一定达到最大。

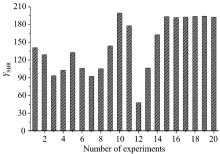
根据先前的研究[15, 20], 选取国家标准土壤样品(编号GBW07410)为研究对象, 其内部主要元素(硅、 铁、 镁、 钙、 铝、 钠、 钾等)以化合物形式存在[20], 如SiO2, Fe3O4, FeO, MgO, CaO, Al2O3, Na2O, K2O等。 根据标准物质元素含量和LIBS发射谱线, 分别选取每种元素的一条发射谱线(Si Ⅰ 390.55 nm, Fe Ⅰ 404.58 nm, Mg Ⅰ 518.36 nm, Ca Ⅱ 393.37 nm, Al Ⅰ 394.40 nm, Na Ⅰ 588.99 nm, K Ⅰ 766.49 nm)为特征分析谱线(Ⅰ 表示元素原子谱线, Ⅱ 表示一次离子谱线)。 为了实现多元素的同时分析, 定义多元素的组合信背比如式(2)

YSBR=∑i=1αISignal(λi)IBackground(λi)(2)

其中: YSBR为选取的多条谱线的组合信背比, λ i为分析谱线的波长, α 为同时考虑的待分析谱线个数, ISignal(λ i)为待分析谱线的光谱强度, IBackground(λ i)为待分析谱线的背景强度。 将YSBR作为目标函数能够同时考虑多条分析谱线的性能, 从而实现多元素同时分析。 根据试验结果, 计算得到目标函数组合信背比YSBR的结果, 如图2所示。

图2 目标函数YSBR的计算结果Fig.2 Results of objective function YSBR

根据图2可以看出, 前面的14次试验(1#— 14#)由于不同的LE, DT和LTSD参数取值, 目标函数YSBR的值发生变化, 说明三者对YSBR有一定的影响作用。 后面的6次试验(15#— 20#)中, LE, DT和LTSD三个参数取值一定, YSBR基本保持不变。

2.3 试验结果分析

经过以上试验设计, 并对结果进行分析, 可以得到YSBR关于LE, DT和LTSD三个参数的回归方程(3)

YSBR=-21 133.584 19+430.901 22× LTSD-20.063 91× DT+6.076 23× LE+1.409 84× LTSD× DT-0.017 377× LTSD× LE+0.196 21× DT× LE-2.217 24× LTSD2-23.636 62× DT2-0.024 009× LE2 (3)

从式(3)看出, LE, DT和LTSD三个参数的线性、 交互和曲面效应对YSBR都有不同程度的影响。 在响应面分析中对试验结果进行拟合和拟合系数的显著性分析, 具体结果见表2。

表2 试验设计的拟合模型方差分析与回归系数的显著性检验 Table 2 Analyses of variance (ANOVA) for regression model and the test of significance of coefficient in quadratic model

由表2可知, 对该模型进行F检验, F值为5.89, (Prob.> F)=0.0053说明只有0.53%的概率该模型可能会产生主要因为内部无用信息影响。 另外, 模型的失拟性(lack of fit)检验是显著的(Prob.> F< 0.000 1< 0.05), 说明拟合的结果很适合表达目标函数。 同时根据拟合结果, 对模型组合信背比YSBR的响应面模型的决定系数R2=0.841 2, 说明本模型能解释84.12%响应值的变化情况, 试验误差较小, 模型拟合度较好。 精度(信噪比)为7.609, 意味着这个模型足够用来对组合信背比YSBR进行分析和预测。

表2显示, 对于模型的回归系数项来说, 因素DT对模型的组合信背比YSBR的线性效果显著(Prob.> F=0.005 0< 0.05), 而因素LTSD和LE的线性效果不显著(因素LTSD: Prob.> F=0.505 8> 0.05, 因素LE: Prob.> F=0.412 9> 0.05); 对于乘积项LTSD× DT, LTSD× LE, DT× LE对组合信背比YSBR的交互效果都不显著(乘积项LTSD× DT: Prob.> F=0.664 0> 0.05, 乘积项LTSD× LE: Prob.> F=0.882 4> 0.05, 乘积项DT× LE: Prob.> F=0.411 8> 0.05); 对于二次项LTSD2, DT2和LE2对模型组合信背比YSBR的曲面效应显著(二次项LTSD2: Prob.> F=0.048 1< 0.05、 二次项DT2: Prob.> F=0.000 5< 0.05和二次项LE2: Prob.> F=0.003 1< 0.05), 将不显著的系数项进行剔除, 然后得到简化的二次回归方程, 如等式(4)所示

YSBR=-21133.58419-20.06391×DT-2.21724×LTSD2-23.63662×DT2-0.024009×LE2(4)

为了确定各个变量对目标函数组合信背比YSBR的影响, 将涉及的三个变量中, 一个变量固定, 改变其余两个变量, 则每组试验方案的响应值YSBR成为两个变量的函数, 由此对YSBR绘制三维曲面图和二维等高线图, 以确定最佳因素水平范围。

图3显示了激光能量(LE)在105 mJ条件下, 延迟时间(DT)与透镜待样品的距离(LTSD)对组合信背比的交互影响。 随着LTSD和DT的增加, YSBR出现上升趋势, 随着二者的继续增加, YSBR反而出现降低。 这说明LTSD和DT之间存在显著的交互影响, 不同的LTSD和DT组合, 将出现不同的YSBR值。 当LTSD为97.68 mm且DT为2.92 μ s时, 得到的组合信噪比最大YSBR为198.52。

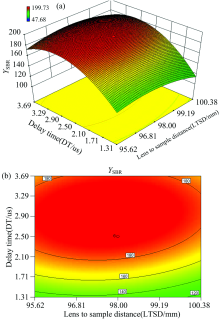图3 DT与LTSD对YSBR交互影响的三维曲面图和等高线图Fig.3 3D surface and counter plots of mutual-influence for DT and LTSD on YSBR

图4显示了延迟时间(DT)在2.5 μ s条件下, 激光能量(LE)与透镜待样品的距离(LTSD)对组合信背比的交互影响。 随着LE和LTSD的增加, YSBR出现增大趋势, 随着二者的继续增加, YSBR反而变小。 这说明LE和LTSD之间存在显著的交互影响, 不同的LE和LTSD组合, 将出现不同的YSBR值。 当LTSD为97.56 mm且LE为101.21 mJ时, 得到的组合信噪比最大YSBR为194.59。

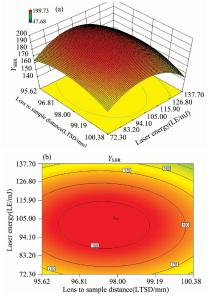图4 ME与LTSD对YSBR交互影响的三维曲面图和等高线图Fig.4 3D surface and counter plots of mutual-influence for LE and LTSD on YSBR

图5显示了透镜到样品的距离(LTSD)在98 mm条件下, 延迟时间(DT)与激光能量(LE)对组合信背比的交互影响。 随着DT和LE的增加, YSBR呈现增大趋势, 随着二者的继续增加, YSBR反而降低。 这说明DT和LE之间存在显著的交互影响, 不同的DT和LE组合, 将出现不同的YSBR值。 当DT为2.91 μ s且LE为102.98 mJ时, 得到的组合信噪比为最大YSBR为198.39。

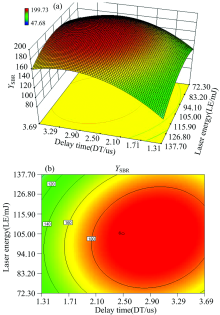图5 LE与DT对YSBR交互影响的三维曲面图和等高线图Fig.5 3D surface and counter plots of mutual-influence for LE and DT on YSBR

通过优化, 使每个影响因素(激光能量LE, 延迟时间DT和透镜到样品的距离LTSD)的期望是响应值(组合信背比YSBR)得到最佳结果。 通过建立非线性优化模型, 最佳的试验条件是: 激光能量LE为103.09 mJ, 延迟时间DT为2.92 μ s, 透镜到样品的距离LTSD为97.69 mm时, 得到最大组合信背比YSBR为198.61。

3 结 论

利用响应面分析法设计了主要三因素(脉冲能量LE, 延迟时间DT和聚焦透镜到样品的距离LTSD)二次回归旋转组合的试验, 讨论了三因素之间交互作用对土壤等离子体特性的影响, 并对试验的参数进行了优化。 以土壤中七种主要元素的谱线组合信背比(signal-background-ratio, SBR)YSBR为目标函数, 分析了三因素之间交互作用对YSBR的影响。 结果表明: DT对YSBR的线性效果显著, 而LE和LTSD对YSBR的线性效果均不显著; 三者的交互影响对YSBR的交互效果都不显著; LE2, DT2和LTSD2对YSBR的曲面效应均显著。 通过分析优化得到最佳的试验条件是: 激光能量LE为103.09 mJ, 延迟时间为2.92 μ s, 透镜到样品的距离LTSD为97.69 mm时, 得到最大组合信背比YSBR为198.602。

本研究为实地田间土壤LIBS检测参数的选择和优化提供了重要的借鉴, 同时为提高LIBS系统对土壤理化信息测定的准确性和稳定性提供了方法和理论指导。 在今后的研究中, 可以尝试重构实地(农田、 果园等)野外测试条件, 并构造基于LIBS技术的标准校正元素特征分析谱线及含量预测-反演模型和方法等, 以实现对待测物的实时原位检测, 并为后期研发物质元素原位技术和装备提供理论基础与技术支撑。

The authors have declared that no competing interests exist.

参考文献
[1] Fortes F J, Moros J, Lucena P, et al. Analytical Chemistry, 2013, 85: 640. [本文引用:2]
[2] Hahn D, Omenetto N. Applied Spectroscopy, 2010, 74: 335A. [本文引用:2]
[3] Hahn D W, Omenetto N. Applied Spectroscopy, 2012, 66: 347. [本文引用:2]
[4] Noll R. Laser-Induced Breakdown Spectroscopy Fundaments and Application. Berlin Heidelberg: Springer-Verlag, 2012. 17. [本文引用:1]
[5] Musazzi S, Umberto P. Laser-Induced Breakdown Spectroscopy Theory and Application. Berlin Heidelberg: Springer-Verlag, 2014. 91. [本文引用:1]
[6] Tognoni E, Palleschi V, Corsi M, et al. Spectrochimica Acta Part B, 2002, 57: 1115. [本文引用:1]
[7] Unnikrishnan V K, Choudhari K S, Kulkarni S D, et al. RSC Advances, 2013, 3: 25878. [本文引用:1]
[8] ZHANG Shu-wei, WU Wei( 张树玮, 吴伟). Physics Experimentation(物理实验), 2015, 35(8): 5. [本文引用:1]
[9] Nicolodelli G, Senesi G S, Romano R A, et al. Spectrochimica Acta Part B, 2015, 111: 23. [本文引用:1]
[10] SUN Lan-xiang, XIN Yong, CONG Zhi-bo(孙兰香, 辛勇, 丛智博, 等). Acta Optical Sinica(光学学报), 2014, 34(5): 284. [本文引用:1]
[11] Kim G, Kwak J, Kim K R, et al. Journal of Hazardous Materials, 2013, 263: 754. [本文引用:1]
[12] de Carvalho G G A, Santos D, Gomes M D, et al. Spectrochimica Acta Part B, 2015, 105: 130. [本文引用:1]
[13] Gomes M D, Santos D, Nunes L C, et al. Talanta, 2011, 85: 1744. [本文引用:1]
[14] Fedotova N, Kaegi R, Koch J, et al. Spectrochimica Acta Part B, 2015, 103: 92. [本文引用:1]
[15] Yu K-Q, Zhao Y-R, Liu F, et al. Scientific Report, 2016, 6, 27574, doi: DOI:10.1038/srep27574. [本文引用:2]
[16] Myers W R. Encyclopedia of Biopharmaceutical Statistics. New York: Marcel Dekker, 2003. [本文引用:2]
[17] Iqbal M, Iqbal N, Bhatti I A, et al. Ecological Engineering, 2016, 88: 265. [本文引用:2]
[18] Jacob S, Banerjee R. Bioresource Technology, 2016, 214: 386. [本文引用:2]
[19] LI Yun-yan, HU Chuan-rong(李云雁, 胡传荣). Experiment Design and Data Processing(试验设计与数据处理). 3rd ed. (第3版). Beijing: Chemical Industry Press(北京: 化学工业出版社), 2008. 131 [本文引用:1]
[20] YU Ke-qiang, HE Yong, LIU Fei(余克强, 何勇, 刘飞). Transactions of the Chinese Society of Agricultural Engineering(农业工程学报), 2015, 31(12): 1. [本文引用:2]