宜兴市地处江苏省南部(31° 07'— 31° 37'N, 119° 31'— 120° 03'E), 属亚热带季风区, 四季分明, 年平均气温16 ℃, 年平均降水量1 498.8 mm。 该市南部为低山丘陵, 北部为平原低洼, 土地肥沃, 主要植被种类包括北部的水稻、 小麦、 茶叶等农作物和南部的毛竹等林木。

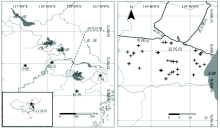
2010年8月11日— 14日采集了包括水稻(14个)、 玉米(13个)、 芝麻(12个)、 大豆(11个)、 茶叶(11个)、 草地(13个)、 乔木(10个)和灌木(11个)在内的八种植被共计95个叶片样本, 每类植被中的样本点均随机选取(图1), 采样时记录下每个样本点的地理坐标, 并将剪下的新鲜植被叶片用塑料袋保存好, 当天送回实验室进行室内分析。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 研究区域(a)和采样点(+)分布图(b)Fig.1 Maps showing the Yixing region in China (dashed area) (a) and the distribution of sampling sites (+) (b)

采用ASD FieldSpec3地物光谱仪测量植被叶片反射光谱。 光谱范围为350~2 500 nm, 其中350~1 000 nm之间采样间隔为1.4 nm, 1 000~2 500 nm之间为2 nm。 光谱测量在暗室进行, 将当天采集的新鲜叶片样本均匀铺盖在无反射的黑色托盘内, 采用50 W卤素灯作唯一光源, 光源距离样本中心30 cm, 入射角为15° , 光谱仪探头位于样本垂直上方15 cm, 其视场角为25° 。 测试前先对仪器进行标准白板校正, 测试过程中每测六个样本便重新校正一次, 确保测量稳定。 每个样本采集10条光谱曲线, 进行算术平均, 得到样本点的光谱反射率数据。

植被叶片样本经过光谱测量后, 分别进行叶片氮、 磷、 钾元素含量的化学分析。 其中叶片中氮元素的含量采用凯氏定氮法测定, 磷元素的含量采用钼锑抗比色法测定, 钾元素的含量采用火焰光度计法测定^[8]。

对分析得到的氮、 磷、 钾元素含量数据分别进行异常点检测, 当某一样本落在样本集学生化残差± 2.5范围之外且大于两倍平均杠杆值时, 将其视作异常点予以剔除, 以此确保模型的准确度。 经计算, 氮元素样本集中剔除了两个异常点, 磷元素样本集中剔除了两个异常点, 钾元素样本集中剔除了两个异常点。

去除叶片反射光谱中噪声较大的350~399和2 401~2 500 nm边缘波段, 选取400~2 400 nm波段以10 nm为间隔进行重采样, 得到401~2 391 nm波段原始反射光谱。 在结合前人研究的基础之上, 采用三种光谱预处理方法消减背景噪声, 首先对原始反射光谱进行一阶微分变换(first derivative, FD), 随后对一阶微分变换光谱分别采用标准正态变量变换(standard normal variate, SNV)和倒数的对数变换(logrithmic reciprocal transformation, Log(1/R))。 以上光谱预处理运用Parles V3.0软件完成。

1.4.1 支持向量回归及核函数

支持向量模型可表述为

f(x)=∑i=1naiyiK(xi, x)-b, 0≤ai≤C(1)

式中K(x_i, x)为核函数, x_i为输入向量(本研究中为光谱反射率数据), x是用于计算更高维特征空间的数据项, y_i为输出向量(本研究中为生化组分含量), a_i为拉格朗日因子矩阵, n为样本数量, b为残差, C为正则化参数, 用以控制超出误差的样本的惩罚程度。 核函数可将非线性关系映射到高维空间中, 构建线性回归进行处理, 本研究分别采用了多项式核函数[式(2)], 径向基核函数[式(3)]和S形核函数[式(4)]

K(xi, x)=(k< xi, x> +c)d(2)K(xi, x)=exp-‖xi, x‖22σ2(3)K(xi, x)=tanh(k'< xi, x> +ϑ)(4)

其中c, d, k, σ , ϑ 和k'等核函数中的参数由优化算法确定^[11]。

1.4.2 模型建立与验证

从样本集中随机选取70%(65个)样本作为校正集, 针对每一种核函数, 在Matlab2010b环境下利用LIBSVM工具箱进行支持向量回归模型的校正^[12]。 三种核函数中的参数采用网格参数寻优法和五折交叉验证确定, 取交叉验证过程中均方根误差(root mean square error, RMSE)最小时所对应的各参数为最优值^[8]。 剩余30%(28个)样本作为验证集, 以检验校正所得SVR模型的表现, 模型精度评价指标采用决定系数(determination coefficient, R²)和相对分析误差(ratio of performance to standard deviate, RPD)。 上述评价指标中, R²越大, 模型预测效果越好, 此外, 当RPD在1.4~2时, 表示模型有一定的预测能力, 在2~2.5时表示模型预测能力良好, 大于2.5时则表明模型有很好的预测能力。

为减少随机抽样建模所导致的误差, 采用bootstrapping方法, 对原始93个样本进行有放回的抽样, 获得1000组校正集和验证集, 将上述模型校正和验证流程重复1 000次, 并计算出1 000次模型校正和验证的R²均值与RPD均值, 用以评价基于不同核函数的模型表现。

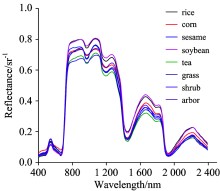
植被叶片样本生化组分含量统计如表1所示, 不同种类植被叶片的氮、 磷、 钾元素含量差异较大, 可达10倍以上。 八种植被叶片的平均反射光谱曲线总体形态比较一致, 反射率高低存在差异, 如图2所示。 其中在550 nm附近因叶绿素的弱吸收而形成反射峰, 700至750 nm区间内出现反射率增长最快的“ 红边” (red edge), 780~1 300 nm近红外波段区间反射率较高, 主要是叶片细胞组织反射造成, 1 450和1 950 nm附近的反射谷则主要是由水分的吸收引起。

表1

Table 1

表1(Table 1)

表1 植被叶片样本氮、 磷、 钾元素含量统计 Table 1 Descriptive statistics of the contents of nitrogen (cN), phosphorus (cP) and potassium (cK) of plant leaf samples 样本数 均值 标准差 最小值 中值 最大值 cN/% 93 2.406 8 0.976 2 0.319 8 2.494 8 5.099 8 cP/% 93 0.169 2 0.124 3 0.000 7 0.161 2 0.583 5 cK/% 93 1.701 8 0.811 7 0.465 8 1.623 6 4.481 5

表1 植被叶片样本氮、 磷、 钾元素含量统计 Table 1 Descriptive statistics of the contents of nitrogen (cN), phosphorus (cP) and potassium (cK) of plant leaf samples

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 八种植被叶片平均反射光谱曲线Fig.2 The average original reflectance spectra of leaf samples from eight kinds of plants

对植被叶片氮、 磷、 钾元素含量与预处理光谱及原始光谱的相关关系进行分析, 其结果如图3所示。 叶片原始光谱与各生化组分含量之间的相关系数都比较小(c_N: -0.22~0.20, c_P: -0.21~0.19, c_K: -0.37~0.12), 经预处理后的光谱与三种含量之间的相关系数都有显著增大, 某些波段达到0.05显著性水平。 而三种预处理方法对相关关系的提升作用相当, 与一阶微分变换相比(最大相关系数分别为c_N: 0.54, c_P: 0.63和c_K: -0.66), 进一步采用SNV变换或Log(1/R)变换仅略微提高相关关系(< 0.03)。

图3

Fig.3

Figure Option ViewDownloadNew Window

图3 植被叶片cN, cP, cK与预处理光谱的相关性 注: 虚线代表生化组分含量与原始光谱的相关性(a): 一阶微分变换与cN; (b): 一阶微分和SNV变换与cN; (c): 一阶微分和Log(1/R)变换与cN; (d): 一阶微分变换与cP; (e): 一阶微分和SNV变换与cP; (f): 一阶微分和Log(1/R)变换与cP; (g): 一阶微分变换与cK; (h): 一阶微分和SNV变换与cK; (i): 一阶微分和Log(1/R)变换与cKFig.3 Correlations of the contents of nitrogen (cN), phosphorus (cP) and potassium (cK) against the original reflectance (dash line) and their derived values with different pre-processing methods Note: the dashed lines refer to the correlations between the biochemical components and original reflectance spectra (a): First derivative; (b): first derivative plus standard normal variate (SNV); (c): First derivative plus absorbance transformation (Log(1/R)) for cN; (d): First derivative; (e): First derivative plus SNV; (f): First derivative plus Log(1/R) for cP; (g): First derivative; (h): First derivative plus SNV; (i): First derivative plus Log(1/R) for cK

利用三种不同预处理方法和三种核函数, 建立支持向量机回归模型估算植被叶片氮、 磷、 钾元素含量, 其结果如表2所示。 总体上看, 基于RBF核函数模型的精度最佳, 多项式核函数模型结果次之, 而S形核函数模型效果最差。 模型校正结果显示, 基于一阶微分变换的RBF核函数模型对三种组分含量的反演结果最优; 模型验证结果表明, 基于一阶微分和Log(1/R)变换的RBF核函数模型对氮、 钾元素含量的反演精度最佳(c_N: 平均R²=0.64, 平均RPD=1.67; c_K: 平均R²=0.56, 平均RPD=1.48), 而基于一阶微分变换的RBF核函数模型则是磷元素的最佳估算模型(平均R²=0.68, 平均RPD=1.73)。 分别选出验证过程中R²最高的模型, 其对生化组分含量的预测值与实测值在0.05显著性水平下均存在强相关性(c_N: R²=0.85, RPD=2.63; c_P: R²=0.87, RPD=2.80; c_K: R²=0.83, RPD=2.30), 如图4所示。

表2

Table 2

表2(Table 2)

表2 基于径向基核函数、 S形核函数和多项式核函数的植被叶片cN, cP, cK估算SVR模型结果 Table 2 Performances of support vector regression models with radial basis function kernel, sigmoid kernel and polynomial kernel for estimating the contents of nitrogen (cN), phosphorus (cP) and potassium (cK) of plant leaves FD FD+SNV FD+Log(1/R) RBFa Sigb Polyc RBF Sig Poly RBF Sig Poly cN R2* 0.93 0.84 0.88 0.92 0.80 0.89 0.91 0.80 0.89 RPD* 7.80 2.97 3.62 5.78 2.78 4.23 4.19 2.66 3.40 RV2* * 0.58 0.56 0.58 0.60 0.58 0.61 0.64 0.59 0.60 RP DV* * 1.51 1.47 1.51 1.55 1.50 1.56 1.67 1.52 1.59 cP R2 0.99 0.83 0.83 0.89 0.72 0.75 0.94 0.78 0.85 RPD 32.97 3.04 4.30 6.17 2.05 2.18 15.95 2.59 3.54 RV2 0.68 0.53 0.50 0.54 0.51 0.52 0.57 0.54 0.56 RPDV 1.73 1.40 1.34 1.44 1.34 1.39 1.47 1.40 1.44 cK R2 0.94 0.75 0.78 0.89 0.73 0.75 0.87 0.69 0.76 RPD 11.04 2.11 2.43 6.17 2.05 2.18 4.35 1.97 2.26 RV2 0.55 0.50 0.52 0.54 0.51 0.52 0.56 0.48 0.52 RPDV 1.46 1.37 1.39 1.44 1.38 1.39 1.48 1.34 1.39 a RBF: 径向基核函数; b Sig: S形核函数; c Poly: 多项式核函数; * R2: 校正集平均决定系数; * RPD: 校正集平均相对分析误差; * * RV2: 验证集平均决定系数; * * RPDV: 验证集平均相对分析误差

表2 基于径向基核函数、 S形核函数和多项式核函数的植被叶片cN, cP, cK估算SVR模型结果 Table 2 Performances of support vector regression models with radial basis function kernel, sigmoid kernel and polynomial kernel for estimating the contents of nitrogen (cN), phosphorus (cP) and potassium (cK) of plant leaves

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 验证过程中R2最高模型的预测表现 (a): cN; (b): cP; (c): cKFig.4 Performance of the best models for estimating the contents of nitrogen (cN) (a), phosphorus (cP) (b) and potassium (cK) (c) with the validation dataset

基于RBF核函数的SVR模型对植被叶片氮、 磷、 钾元素含量的预测优于S形核函数和多项式核函数模型。 植被叶片生化组分含量与其VNIR光谱之间的关系通常是非线性的, 且会受到叶片生化组分特征及实验条件的影响。 RBF核函数(也称高斯核函数)能够实现高维空间的非线性映射, 即使在样本分布未知情况下, 其旋转对称性可确保不造成大的偏差^[5], 而S形核函数在某些参数条件下不满足核函数半正定性要求, 其应用会受到限制^[13]。 此外, 与多项式核函数和S形核函数相比, RBF核函数的待优化参数较少, 模型复杂度更低, 稳健性更好。 综合他人研究^[6]和本实验结果, 基于VNIR光谱和支持向量机进行植被叶片生化组分含量估算时, 可优先考虑RBF核函数。

传统的估算植被生化参数方法包括多元线性回归(MLR)和偏最小二乘回归(PLSR)。 多元线性回归法一般选择若干个波段参与运算, 但波段选择没有考虑植被的吸收特征, 容易忽略与目标参数密切相关的光谱信息; 偏最小二乘回归是多元线性回归与主成分分析(PCA)的组合, 克服了波段选择和多元共线性的不足, 但与多元线性回归同属线性方法, 对非线性关系的处理能力有限^[6]。 本工作所用的支持向量机回归方法, 通过合适的核函数将非线性关系映射到高维空间, 可有效处理变量间非线性关系; 若干研究对比了PLSR和SVR对非线性关系数据的建模预测能力, 发现SVR表现更佳^{[6, 14]}。 人工神经网络(ANN)法在处理非线性问题时同样有较好的效果^[15], 但其存在模型物理意义不明、 模型过拟合等不足^[7]。 因此, 在利用植被叶片光谱进行生化组分参数估算时, 基于RBF核函数的支持向量机回归模型具有很大潜力。

基于RBF核函数的支持向量机回归模型, 针对八种不同植被叶片的光谱数据, 估算氮、 磷、 钾等三种元素含量的平均精度为0.64, 0.68和0.56, 最佳精度可达0.85, 0.87和0.83。 Yao等^[7]利用支持向量机方法估算小麦叶片氮含量的精度可达0.78, Axelsson等^[14]结合各种支持向量机方法基于景观尺度的红树林高光谱数据反演其叶片的氮、 磷、 钾、 钙等化学元素的含量, 发现只有氮元素的反演结果令人满意(R²=0.67)。 与这些研究相比, 本工作所得模型精度适中, 稳健性较好, 表明建立一个针对混合植被类型的多生化参数估算模型是可以实现的。 然而本研究采用的是基于植被叶片尺度的室内光谱测量, 对模型在不同季节, 不同尺度, 不同光谱数据时的适用性, 还需进一步验证; 同时, 对于其他潜在的光谱预处理方法和核函数模型, 也有待进一步探究比较。