引用本文
郭志卫, 孙兰香, 张鹏, 齐立峰, 于海斌, 曾鹏, 周中寒, 汪为, 史友振. 基于LIBS技术的水泥粉末在线成分分析[J]. 光谱学与光谱分析, 2019,39(1): 278-285.
GUO Zhi-wei, SUN Lan-xiang, ZHANG Peng, QI Li-feng, YU Hai-bin, ZENG Peng, ZHOU Zhong-han, WANG Wei, SHI You-zhen. On-Line Component Analysis of Cement Powder Using LIBS Technology[J]. Spectroscopy and Spectral Analysis, 2019,39(1): 278-285.
Doi:10.3964/j.issn.1000-0593(2019)01-0278-08  
Permissions
Copyright©2019, 《光谱学与光谱分析》期刊社
《光谱学与光谱分析》期刊社 所有
基于LIBS技术的水泥粉末在线成分分析
郭志卫1,2, 孙兰香1,*, 张鹏1,3, 齐立峰1, 于海斌1, 曾鹏1, 周中寒1,3, 汪为1,3, 史友振1,4
1. 中国科学院沈阳自动化研究所工业控制网络与系统研究室, 辽宁 沈阳 110016
2. 东北大学信息科学与工程学院, 辽宁 沈阳 110819
3. 中国科学院大学, 北京 100049
4. 沈阳建筑大学, 辽宁 沈阳 110168
*通讯联系人 e-mail: sunlanxiang@sia.cn

作者简介: 郭志卫, 1991年生, 中国科学院沈阳自动化研究所工业控制网络与系统研究室硕士研究生 e-mail: guozhiwei@sia.cn

收稿日期: 2017-08-14 接受日期: 2018-01-09
基金: 国家自然科学基金项目(61473279), 国家重点研发计划项目(2016YFF0102502, 2017YFF0106202), 中国科学院前沿科学重点研究计划(QYZDJ-SSW-JSC037), 中国科学院青年创新促进会资助
摘要

在工业现场生产水泥的过程中, 各种成分的含量直接影响着水泥的质量, 因此如何快速准确地监测水泥中各个成分的含量意义重大。 采用的实验方式为, 将不经过任何预处理的水泥粉末直接放入位于二维移动平台上的物料盒中, 通过激光诱导击穿光谱(LIBS)直接对水泥粉末表面的不同位置进行激发检测, 对得到的光谱数据首先进行归一化和主成分分析等预处理操作, 然后针对水泥中Ca, Si, Al, Fe, Mg五种元素, 分别建立偏最小二乘(PLS)和支持向量回归(SVR)两种定量分析模型进行方法比较。 此外, 对比了粉末状水泥与压片式水泥两种测量方式的结果。 实验结果表明, 采用粉末状水泥直接测量的方式下, 针对水泥样品元素浓度与所得到的光谱中特征线强度的关系, SVR方法比PLS方法更具优势, 粉末状水泥直接测量的精度接近压片式测量的精度, 说明LIBS技术对水泥粉末状样品直接在线测量具有可行性。

关键词: 激光诱导击穿光谱; 偏最小二乘法; 支持向量回归; 主成分分析; 水泥
中图分类号:TN206 文献标志码:A
On-Line Component Analysis of Cement Powder Using LIBS Technology
GUO Zhi-wei1,2, SUN Lan-xiang1,*, ZHANG Peng1,3, QI Li-feng1, YU Hai-bin1, ZENG Peng1, ZHOU Zhong-han1,3, WANG Wei1,3, SHI You-zhen1,4
1. Laboratory of Industrial Control Network and System, Shenyang Institute of Automation, Chinese Academy of Sciences, Shenyang 110016, China
2. College of Information Science and Engineering, Northeastern University, Shenyang 110819, China
3. University of Chinese Academy of Sciences, Beijing 100049, China
4. Shenyang Jianzhu University, Shenyang 110168, China
Abstract

In the process of cement production in the industrial field, the content of each component in the cement directly affects the quality of the cement. Therefore, it is of great significance to quickly and accurately monitor the content of each component in the cement. In this paper, the laser induced breakdown spectroscopy (LIBS) technology is used to detect the powder cement, and the powder cement are put in a two-dimensional moved platform without any pretreatment. The spectral data is processed by normalization and principal component analysis(PCA) firstly, which is used as the input of the model. In order to analyze the elements of Ca, Si, Al, Fe and Mg in cement, we build the models based on Partial least squares(PLS) and Support Vector Regression (SVR) as the comparison of methods. In addition, the comparison of measurement methods is between cement powder detection and cement tablet detection. The experimental results show that in this type of experiment, the SVR method is more advantageous than the PLS method because of the relationship between the element concentration and the strength of its characteristic line of the cement samples. The accuracy of the direct measurement of the cement powder is close to that of the tablet type, and it demonstrated the feasibility of on-line analysis of cement powder using LIBS technology under this type of experiment.

Keyword: LIBS; Partial least squares; Support Vector Regression; PCA; Cement
引 言

水泥作为一种重要的建筑材料, 广泛应用于道路、 桥梁、 楼房等建筑中[1]。 在水泥生产中, 组成水泥的成分含量直接影响着水泥的质量, 因此如何保证在水泥生产过程中对其成分含量进行实时监测, 是不可缺少的一个重要环节。 激光诱导击穿光谱(LIBS)技术因分析速度快、 无需样品制备、 可以做到在线检测等优点, 自问世以来就受到越来越广泛的青睐, 具有广阔的发展前景[2, 3]。 在对水泥的成分分析方面, 国内外很多专家学者进行过不同方面的研究。 伊朗的Mansoori等[4]利用LIBS对水泥进行了分析, 讨论了一些实验参数对检测结果的影响; 清华大学的尹华亮等[5]通过改进的光谱标准化方法对水泥生料中影响其质量优劣的三率值进行了研究, 其绝对测量误差在0.01~0.015以内; 山西大学的郭锐等[6]研制出一套基于LIBS的化验室水泥质量检测设备, 对水泥生熟料中CaO, SiO2, Al2O3, Fe2O3成分进行了定量分析, 同时也验证了激光诱导水泥等离子体处于局部热平衡状态; 李文宏等[7]通过循环反演的方法对普通硅酸盐水泥样品中MgO进行了定量分析, 定标曲线的线性系数达到0.995 9, 检测限可以达到0.51%。

前述研究证明了LIBS技术应用于水泥成分的快速分析的可行性, 但是, 这些研究大部分是针对粉末状水泥样品的压片分析。 瞬发伽马射线中子活化分析技术(PGNAA)可以实现粉末状水泥的在线分析, 但设备具有放射源, 而且价格昂贵[8]。 弓瑶等[9]研制了一套基于LIBS的粉末状水泥在线成分分析设备, 但需要通过气动连续取样器对水泥粉末进行取样。 而本研究是基于LIBS对传送带上粉末状水泥样品直接进行测量的可行性评论。

在校准模型上, 采用多变量建模对影响水泥质量的Ca, Si, Al, Fe, Mg五种元素分别进行建模。 与单变量模型相比, 多变量模型考虑了光谱中更多的有用信息, 适应性更强, 精度更高。 在目前应用比较广泛的多变量定量分析方法中, 应用较多的主要包括偏最小二乘(PLS)、 支持向量机(SVM)等, 其中PLS方法在建立线性关系模型方面具有很大优势[10, 11, 12, 13, 14, 15]。 王哲等[16, 17, 18]对不同环境气体下烟煤的LIBS数据进行了偏最小二乘(PLS)建模分析, 并对模型进行了优化改进, 提出了一种基于主导因子的PLS方法, 可以有效降低LIBS测量的不确定性。 支持向量机(SVM)的优势为在样本数据量较小的情况下也能获得好的分析效果, 而且SVM方法对于克服基体效应有明显优势。 张莹等通过支持向量回归(SVR)方法对钢铁合金中的Cr和Ni元素进行了定量分析, 对比了不同输入情况下的模型预测能力, 发现将内标法与多变量定标方法有效结合可以使SVM表现出更好的学习优势; 田野等[19]通过对比PLS-DA和SVM两种方法, 对地质岩屑样品进行了分类研究, 发现SVM方法建立的非线性模型分类准确率要好于PLS-DA, 并且最终将两种方法进行了结合, 得到了更好的分类效果。 除此之外, 很多国内外专家学者也通过相关的研究, 验证了多变量方法对于定量分析的优势。

本工作针对粉末状水泥样品进行实验测量, 同时将压片实验作为对比分析; 将实验得到的原始光谱数据进行预处理, 采用PLS与SVR两种方法对水泥中的主要元素分别建立定量分析模型, 并对两种模型的验证结果进行对比分析。

1 实验部分
1.1 仪器

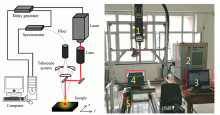
实验装置基本组成如图1所示。 等离子激发源为Nd: YAG激光器, 输出波长为1 064 nm, 最大输出能量为200 mJ, 脉冲激光通过焦距为750 mm的汇聚透镜在样品表面产生等离子体。 探测装置采用波长范围为238~360 nm的Avantes光谱仪, 光学分辨率为0.06 nm, 光谱收集方式采用与激光器激发同等收集, 通过自行研制的多通道时序控制器来控制激光器激发与光谱仪采集之间的时序关系, 时序控制器和光谱仪均放于控制柜中。

图1 LIBS系统原理图(a)和现场系统图(b)
1: 激光器及光学系统; 2: 控制柜; 3: 计算机; 4: 料盒; 5: 二维电动平移台Fig.1 System diagram (a) and on-site system (b)
1: Laser and optical system; 2: Control cabinet; 3: Computer; 4: Sample box; 5: Two-dimensional electric transfer platform

1.2 样品制备

所用的水泥样品是针对6个水泥产地(C30, GH, HK, JG, SN, SYS)的原料组成成分以及各个成分的浓度范围进行制备。 样品中的各个待分析元素是以化合物的方式存在, 分别为CaO, SiO2, Al2O3, FeO, MgO等。 配制的方式为根据组成样品的各个化合物含量按质量百分比进行配制, 搅拌均匀, 共计32个样品, 其微量元素组成存在差异, 在样品的组成成分中, 待分析元素的浓度情况如表1所示。

表1 样品主要成分浓度表 Table 1 The concentration of major components in samples

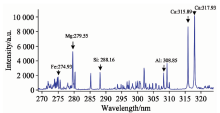
实验过程中, 首先选择不同的激光脉冲能量和采集延迟时间进行实验, 将最佳实验结果对应的参数作为最终的水泥分析实验条件, 即激光脉冲能量为82 mJ, 光谱采集延迟时间为1 μ s。 本实验的最终目的是针对工业现场的粉末状水泥进行在线成分分析, 因此实验时直接将粉末样品倒入盛放样品的容器中, 不做任何处理。 每个位置测一次, 每个样品测1 000个位置; 通过二维位移台的移动进行不同位置的激发; 激光脉冲频率为5 Hz。 除此之外为了验证直接激发粉末样品的可行性, 增加压片式实验作为对比分析。 为了保证数据量的一致性, 压片状态下每个样品激发20个点, 每个点激发50次, 因此两种方式中每个样品均得到1 000组光谱数据。 样品状态如图2所示, 图中左侧部分是粉末状样品实物, 右侧部分为压片状态。 在该实验方式下得到的LIBS光谱信息如图3所示。

图2 样品图Fig.2 Cement samples

图3 水泥样品等离子体光谱图Fig.3 Plasma spectra of cement sample

2 模 型
2.1 数据预处理

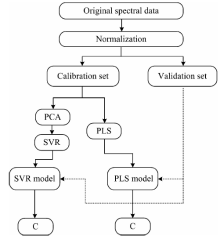
模型的输入对于模型的整体表现起到了至关重要的作用, 因此在建立模型之前需要对原始光谱数据进行预处理。 在此原始数据的预处理包括求平均、 归一化、 主成分分析三部分。

2.1.1 原始光谱求平均

由于粉末样品过于松散, 不同位置的光谱激发情况波动很大, 导致检测数据重复性差, 影响数据的准确性, 单张光谱无法体现样品真实浓度信息, 因此选择每200个位置的光谱作一次平均, 以减少不同位置的波动导致的误差。 由于压片式实验作为对比, 为了保证相同的数据量, 压片方式中每4个位置(共计4× 50=200)作一次平均, 因此每种实验方式下每个样品最终均得到5组光谱数据, 32个样品最终得到160组光谱数据用于模型训练与验证。

2.1.2 数据归一化

在光谱区间内Ca元素有波长为315.89和317.89 nm的两条特征线, 分别将单根特征线强度和两根特征线强度均值进行归一化, 对比试验结果, 两根特征线强度均值方式效果更好, 因此选择这两条特征线强度的均值作为内标强度进行归一化处理。 选择该方式处理的原因在于, 水泥中元素组成是以CaO为主, 假设同一个样品中CaO的浓度变化可以忽略, 即假设样品中元素浓度均匀, 通过该内标方式的预处理, 可以一定程度上克服光谱信号波动的影响。 处理可以用式(1)表示。

Xi=xix̅i(1)

式(1)中xi为第i组光谱数据, x̅i为第i组光谱数据中两条Ca特征线的平均强度, Xi则为经过预处理后的光谱数据。

2.1.3 主成分提取

完整的光谱数据为2 048维, 若将全谱作为输入, 不利于模型的建立, 会带来更多的干扰, 致使模型不能达到有效的训练效果。 因此通过主成分分析对数据进行降维, 通过粒子群(PSO)优化方法对主成分个数进行优化, 选出的最优主成分数为4, 将每组经过主成分提取的4维光谱数据作为SVR的输入来建立模型。 由于PLS方法包括主成分提取, 因此PLS方法的输入是2 048维的归一化数据, 只需要选择和主成分分析相同的主成分数即可。

2.2 模型建立

2.2.1 偏最小二乘(PLS)

偏最小二乘法是一种新型的多元统计数据分析方法, 主要包括主成分分析、 典型相关分析和多元线性回归, 其原理在于建立自变量与因变量的之间的线性回归模型为式(2)所示

Y=XB+E(2)

式(2)中Y是具有m个变量、 n个样本点的响应矩阵, X是具有p个变量、 n个样本点的输入矩阵, B是回归系数矩阵, E为噪音校正模型, 与Y具有相同的维数。

将经过预处理后的光谱数据作为模型的自变量输入X, 待分析元素的浓度作为因变量来建立标定模型, 通过选取合理的主成分数来优化模型的预测能力。 与单变量方法相比, PLS方法中利用了更多的变量, 能够更全面的获取光谱中的有用信息, 增加模型的可靠性, 更适用于基体效应复杂的定量分析。

2.2.2 支持向量回归(SVR)

支持向量回归(SVR)是以统计学理论为基础, 通过将输入数据进行非线性变换转换到高维空间, 在高维空间中构造出线性决策函数来实现线性回归, 并且用核函数代替线性方程中的线性项可以使原来的线性算法非线性化, 可以做非线性回归, SVR能够很好地解决“ 过学习” 和“ 维数灾难” 问题,

尤其处理小样本数据时更凸显其优势。 本工作所使用的SVR模型为式(3)

c=∑i∈Mαi×exp-‖Ii-I‖2γ2+b(3)

式(3)中c为元素浓度, M为支持向量集, α i和Ii分别为拉格朗日乘子和支持向量, I为经过主成分提取后的输入数据, b为常数。 选择的核函数exp -‖Ii-I‖γ2为RBF核函数, 通过粒子群优化(PSO)方法对支持向量集和核参数进行寻优, 以此来使模型达到最佳状态。

2.3 算法结构

基于上述数据预处理以及对PLS模型和SVR模型的描述, 本实验所采用的算法结构如图4所示, 在此算法结构上建立水泥中Ca, Si, Al, Fe, Mg元素的定量分析模型。

图4 算法结构图Fig.4 Algorithm structure diagram

3 结果与讨论

为了分析模型的整体表现, 主要通过决定系数(R2), 相对标准偏差(RSD), 均方根误差(RMSE)三个指标作为参考, 各个指标的计算公式如下

R2=1-∑(Yi-Y˙i)2∑(Y˙i-Y̅)2(4)

式(4)中Yi为第i个样本的预测均值, Y˙i为第i个样本的真实值, Y̅为所有样本的均值。

RMSE=∑(y˙i-yi)2n(5)

式(5)中yi为样本的第i次预测值, y˙i为其对应的真实值, n为样本量。

RSD=∑j=1m(yj-y̅)2(m-1)y̅×100%(6)

式(6)中m为每个样本有m组数据, yj为一个样本的第j次预测值, y̅为样品的预测均值。

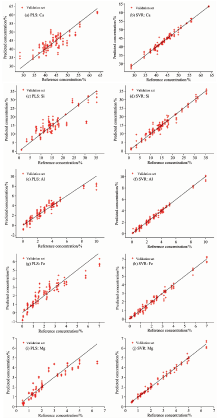
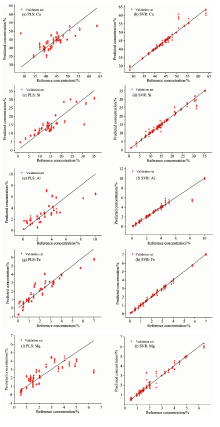
从样品的元素浓度表可以看出, 元素浓度梯度范围很大, 可是分布并不均匀, 出现一定浓度范围的扎堆; 反应出样品量不够充足, 在这种情况下我们采用留一法(leave-one-out)验证模型有效性。 分析结果如图5和图6以及表2所示。

图5 压片状态留一法分析结果Fig.5 Analysis results of leave-one-out for tablet cement

图6 粉末状态留一法分析结果Fig.6 Analysis results of leave-one-out for powder cement

表2 留一法分析结果指标 Table 2 Analysis results of leave-one-out

图5和图6中第一列均为PLS方法的分析结果, 第二列均为SVR方法的分析结果, 不同行代表不同元素的分析结果对比。 表2中第二列的dt和s分别表示粉末式实验和压片式实验, R2, RSD和RMSE均为留一验证所得。 从以上结果中可以看出SVR方法对于验证集的R2基本都能达到0.99, RMSE则能控制在1.3以内, 两个指标均好于PLS方法, 说明在该实验方式下, SVR方法具有更高的预测精度, 更适合用于水泥的分析。 在粉末状态和压片状态的比较中, 表2显示压片状态样品的分析结果普遍好于粉末状样品直接分析的结果, 这与相关的研究相符; 主要是由于粉末样品表面松散, 激光激发到样品表面的状态差异性较大, 具有更大的偶然性。 但是, 从图5和图6的对比中也可以看到, 粉末状样品的测量中有一些偏离参考值较大的异常点, 如果将这些异常点刨除, 粉末状样品直接测量的RSD和RMSE与压片样品的值非常接近。 这说明, 应用LIBS技术对粉末状水泥直接在线测量是具有可行性的, 通过累积大量数据的统计分析和数据预处理, 粉末状水泥直接测量的精度可以接近压片式样品的测量精度。

4 结 论

水泥粉末在不经过压片等处理的情况下放入物料盒中, 通过二维位移台的移动实现不同位置的测量, 为了验证该方式的可行性, 以片状态的实验作为对比分析。 样品针对水泥中Ca, Si, Al, Fe, Mg元素, 建立相应的PLS与SVR定量分析模型, 在两种方法对比中进一步分析该水泥样品的特性。 通过两种分析方法的对比, SVR方法建立的模型相较于PLS有更好的预测结果, 并且当样品量足够多并且浓度分布更加均匀的情况下, 通过SVR方法建立的模型预测能力将会比现在的结果更加理想。 而在水泥样品状态的对比实验中, 由于粉末状样品实验时表面松散, 并且表面状态差异性较大, 在两种模型的分析结果中略差于压片状态, 但是两者差别并不悬殊, 因此可以验证粉末状水泥直接测量的可行性, 并且对于该项技术最终走向工业现场的在线应用具有很好的参考价值。 而对于如何进一步提高现场在线应用实验条件控制, 光谱谱段的选择以及模型的改进, 将是下一步研究的重点。

The authors have declared that no competing interests exist.

参考文献
[1] Aldridge L P. Cement and Concrete Research, 1982, 12(3); 381. [本文引用:1]
[2] Gottfried J L, De Lucia Jr F C, Manson C A, et al. Analytical and Bioanalytical Chemistry, 2009, 395(2): 283. [本文引用:1]
[3] MA De-min, MA Yan-hua, SHU Rong, et al(马德敏, 马艳华, 舒嵘, 等). Infrared and Laser Engineering(红外与激光工程), 2007, 36(5): 656. [本文引用:1]
[4] Mansoori A, Roshanzadeh B, Khalaji M, et al. Optics and Lasers in Engineering, 2011, 49(3): 318. [本文引用:1]
[5] Yin Hualiang, Hou Zongyu, Wang Zhe, et al. Journal of Analytical Atomic Spectrometry, 2016, 31(12): 2384. [本文引用:1]
[6] GUO Rui, ZHANG Lei, FAN Juan-juan, et al(郭锐, 张雷, 樊娟娟, 等). Spectroscopy and Spectral Analysis(光谱学与光谱分析), 2016, 36(7): 2249. [本文引用:1]
[7] LI Wen-hong, WU Zhi-xiang, WANG Rui-wen, et al(李文宏, 武志翔, 王芮雯, 等). Chinese Journal of Lasers(中国激光), 2014, 41(6): 276. [本文引用:1]
[8] Hadad K, Sadeghpour H, Nematollahi M R, et al. Progress in Nuclear Energy, 2016, 90: 204. [本文引用:1]
[9] Zhang Lei, Gong Yao, Li Yufang, et al. Spectrochimica Acta Part B: Atomic Spectroscopy, 2015, 13: 167. [本文引用:1]
[10] SUN Lan-xiang, XIN Yong, CONG Zhi-bo, et al(孙兰香, 辛勇, 丛智博, 等). Acta Optica Sinica(光学学报), 2014, 34(5): 292. [本文引用:1]
[11] Zhang Bo, Yu Haibin, Sun Lanxiang, et al. Applied Spectroscopy, 2013, 67(9): 1087. [本文引用:1]
[12] Kong Haiyang, Sun Lanxiang, Hu Jingtao, et al. Plasma Science and Technology, 2015, 17(11): 964. [本文引用:1]
[13] Boucher T F, Ozanne M V, Carmosino M L, et al. Spectrochimica Acta Part B, 2015, 107: 1. [本文引用:1]
[14] HU Li, ZHAO Nan-jing, LIU Wen-qing, et al(胡丽, 赵南京, 刘文清, 等). Acta Optica Sinica(光学学报), 2015, 35(6): 314. [本文引用:1]
[15] Yang Hongxing, Fu Hongbo, Dong Fengzhong, et al. Chin. Phys. B, 2016, 25(6): 065201. [本文引用:1]
[16] Wang Zhe, Feng Jie, Li Lizhi, et al. Journal of Analytical Atomic Spectrometry, 2011, 26(11): 2302. [本文引用:1]
[17] Feng Jie, Wang Zhe, Li Zheng, et al. Spectrochimica Acta Part B: Atomic Spectroscopy, 2010, 65(7): 549. [本文引用:1]
[18] Feng Jie, Wang Zhe, West L, et al. Analytical and Bioanalytical Chemistry, 2011, 400(10): 3261. [本文引用:1]
[19] Tian Ye, Wang Zhennan, Han Xiaoshuang, et al. Spectrochimica Acta Part B: Atomic Spectroscopy, 2014, 102: 52. [本文引用:1]