光谱观测能够获悉天体各种物理参量信息, 是实测天体物理学的一个重要内容, 具有重要的天文意义。 与之相关的光谱观测仪器也一直是地面大型天文望远镜研制之必备设备。 一米新真空太阳望远镜^[1](new vacuum solar telescope, NVST)是我国新一代地面大型太阳观测设备之一, 是世界上口径最大的真空太阳望远镜, 其主力观测终端为多通道高分辨率成像系统和光谱观测系统, 其中光谱观测系统配有两台大型光栅光谱仪, 能够在可见光及近红外波段对太阳大气进行高时空和高光谱分辨率观测。

不同高度太阳大气同步观测研究是NVST既定的一个科学目标。 太阳色球活动的典型速度超过1.0 km· s^-1, 而光球活动的典型速度在0.1~0.4 km· s^-1左右。 要能使探测到的太阳光球活动现象的物质运动信息真实可信, 则多普勒速度测量误差须不超过30 m· s^-1。 这样的探测精度不仅与多普勒速度测量方法有关, 更与数据的信噪比有关, 然而实际观测中, 光谱数据往往伴随着随机噪声, 传统的光谱数据预处理只是涉及诸多系统误差的改正, 比如平、 暗场处理, 预处理后图像噪声的影响仍然存在。 因此, 对预处理后的光谱数据实行更进一步的处理, 降低噪声的影响显得十分有必要。 此外, 天文观测数据是海量的, 尤其是光谱数据。 对于开放式的天文台站, 有着数据规范发布的需求, 我们希望NVST数据形式简单, 能够直接为天文学家所用。 因此, 要实现NVST光谱数据规范发布, 须对其海量光谱数据进行有效的压缩。

主成分分析(principal component analysis, PCA)是一种经典的数据分析方法, 它通过线性变换提取数据主要特征信息, 最大程度保留数据原有信息, 早先常用于模式识别、 机器学习等领域。 近年来, PCA作为一种常用的特征信息提取方法在天文领域也有应用, 如大规模巡天中星系光谱的识别^[2], 宇宙学统计不确定性约束和信息提取^[3], 太阳质子事件与太阳活动区参量分析^[4]等。 在国外, PCA技术应用于天文光谱数据处理已有成功范例, 如Fiorentin等^[5]就曾利用PCA对斯隆数字化巡天(sloan digital sky survey, SDSS)光谱数据进行降噪处理, Gonzalez等^[6]也曾用PCA对恒星偏振光谱进行过降噪处理, 美国大熊湖天文台快速成像光谱仪^[7](fast imaging solar spectrograph, FISS)也采用PCA技术对光谱数据进行处理。 而在国内, PCA技术应用于天文光谱处理较少, 仅有用于夜天文一维光谱数据处理的报道, 目前暂无应用于太阳光谱数据处理的报道。

根据NVST光谱数据特点, 建立一套基于PCA技术的光谱信号提取方法, 从残余信号的角度研究了参数选择和信息高精度保留方法, 并从科学应用的角度分析了主成分阶数和谱线多普勒速度测量精度的关系。

本组光谱数据图像大小2 004× 668, 总帧数5 314, 选取第一帧光谱图, 按上述步骤进行主成分分析, 依次求得特征向量U_i和特征值λ _i, 得到总共668阶主成分。 表2显示的是前10阶主成分贡献率和累计贡献率的值, 可看到第一阶主成分贡献率高达98.16%, 这说明第一阶主成分已经包含了光谱数据绝大部分信息, 此后各阶主成分贡献率逐渐递减, 当阶数达到580时, 累计贡献率已达99.99%, 基本可认为光谱信息主要集中在前580阶中。 为方便看到主成分贡献率随阶数的变化趋势, 图1显示它们的关系曲线, Y轴以对数显示, 可看到30阶内主成分贡献率降速较快, 超过30阶以后贡献率降速逐渐变缓慢。 取前30阶主成分重构光谱, 将重构出的光谱图与原始光谱图相减, 发现残差图中呈现的主要是干涉条纹和随机噪声, 这说明30阶主成分下, 重构图像已能很好的保留原始光谱图像信息, 干涉条纹及随机噪声能得到有效抑制。 显然, 重构过程中噪声抑制程度和选取的主成分阶数大小有密切关系, 为考察它们之间关系, 计算了各阶重构图像噪声大小, 这里借鉴FISS光谱噪声大小评估方法^[7], 用二阶有限差分的均方根差ε 来评估噪声大小, 在计算ε 的同时, 还计算了各阶重构后残差图像的均方根差σ , 以此来评估残差图像的噪声大小, ε 和σ 计算结果如图2所示, 其中红色虚线表示的是ε 随阶数n的变化曲线, 蓝色实线表示的是σ 随阶数n的变化曲线。 从曲线可以看到, 在低阶段, 随着阶数增大, 残差图像噪声迅速减小, 当阶数达到20, 残差图像噪声减势变缓; 而重构出的图像的噪声一直在稳步增大。 当阶数为668时, 重构图像噪声大小66, 此时重构图像已等同于原始图像。 特别是, 当阶数达到74左右, 残差图像的噪声大小近似等于原始图像噪声大小66, 此时重构图像的噪声大小为20。

表2

Table 2

表2(Table 2)

表2 前10阶主成分贡献率及累计贡献率 Table 2 Contribution rate and cumulative contribution rate of the first 10 order principal components 阶数 贡献率/% 累计贡献率/% 1 98.162 98.162 2 0.490 98.652 3 0.267 98.919 4 0.116 99.035 5 0.053 99.088 6 0.037 99.125 7 0.030 99.155 8 0.019 99.174 9 0.016 99.190 10 0.014 99.204

表2 前10阶主成分贡献率及累计贡献率 Table 2 Contribution rate and cumulative contribution rate of the first 10 order principal components

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 主成分阶数与贡献率曲线Fig.1 The curve of contribution rate with the order of principal component

进一步对5 314帧光谱数据进行分组, 每组按一定帧数组成三维数据, 对三维数据进行特征信息提取实验。 实验中, 按100帧为一组, 计算时, 在100帧光谱数据中抽取了5 000个谱线轮廓向量组成矩阵进行特征分解, 得到特征向量并计算主成分, 并由原始数据和特征向量计算出三维系数矩阵, 最后保存不同阶数下主成分矩阵和对应系数矩阵。 和之前一样, 我们仍取主成分30阶, 由对应系数矩阵重构第一组中的第一帧光谱, 并将重构出的光谱图和原始光谱图相减, 发现残差图像和前述实验中得到的残差图像非常相似, 呈现的主要是干涉条纹和随机噪声, 说明三维数据的主成分分析仍能有良好的降噪效果。 此时, 主成分数组大小2 004× 30, 系数数组大小668× 100× 30, 而原始三维数组大小2 004× 668× 100, 数据压缩比高达64.8。 主成分分析前数据大小510 MB, 主成分分析后数据大小7.9 MB, 数据量大幅缩减。

图2

Fig.2

	Figure Option ViewDownloadNew Window
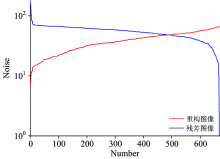	图2 残差图像噪声和重构图像噪声随主成分阶数变化曲线Fig.2 The noise curves of the residual images and the reconstructed images with the order of principal component

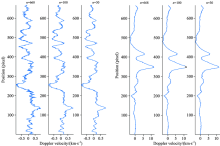
为了评估PCA重构后图像降噪效果, 采用二阶有限差分方法计算噪声大小并计算谱线信噪比。 选取两条代表性的谱线6 569.2和6 562.8 Å , 它们分别来自太阳光球层和色球层, 分别计算了它们各阶主成分重构后谱线信噪比的大小。 所得结果如图3所示, 其中虚线表示光球线6 569.2 Å 的信噪比随PCA重构阶数的变化曲线, 实线表示的是色球线6 562.8 Å 随PCA重构阶数的变化曲线, 两条谱线的信噪比都明显随着阶数的增长而呈下降趋势, 且在低阶段下降较快, 说明低阶段噪声抑制程度较深, 此外光球线的信噪比普遍高于色球线, 这是因为色球线6 562.8 Å 谱线较深, 本身信噪比就要低于光球线6 569.2 Å 。 从曲线看, 当它们各自信噪比达到100时候, 对应重构阶数分别是82和173阶。 我们更关心光谱信息提取后的科学应用问题, 比如太阳不同大气层物质流场信息, 为此我们测量了 PCA 重构后的谱线多普勒速度大小, 图4显示的是不同阶数重构后的两条谱线6 569.2和6 562.8 Å 的多普勒速度曲线, 左边子图对应的是谱线6 569.2 Å , 右边子图对应的是谱线6 562.8 Å , 每个子图中从左至右依次显示的是668, 100和30阶重构后计算得到的曲线。 从图中看到, 随着主成分阶数n变小, 光球线速度曲线中突变的“ 毛刺” 减少, 曲线趋于平滑, 而色球线的变化并不明显, 分析认为相对于色球线 6 562.8 Å , 光球线6 569.2 Å 谱线较浅, 光谱信息提取的效果更加明显, 提取后谱线信噪比明显提高, 从而多普勒速度测量误差更小, 这也从侧面反映了经过PCA信息提取后, 能够探测到更多更浅的谱线, NVST光谱数据科学应用价值增大。 为评估以上多普勒速度测量误差大小, 再次采用二阶有限差分算法计算了图中差分曲线的均方根差, 所得结果见表3所示, 可看到在较小的重构阶数下, 光谱数据的信噪比较高, 多普勒速度测量误差也较小, 测量值的准确度即测量精度也较高, 当主成分阶数为30时, 色球线对应测量精度可达116.6 m· s^-1, 而光球线多普勒速度测量精度高达28.6 m· s^-1, 三倍此测量精度已达到太阳光球活动典型速度, 意味着我们可以有效地探测到太阳光球活动的物质运动信息, 实现太阳光球和色球的同步观测研究。

图3

Fig.3

	Figure Option ViewDownloadNew Window
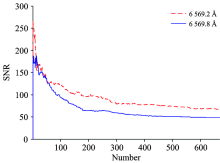	图3 谱线信噪比随PCA重构阶数的变化曲线Fig.3 The changing curves of the signal-to-noise ratio of two spectral lines with the order of PCA reconstruction

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 三种不同PCA阶数重构下计算得到的谱线6 569.2和6 562.8 Å 的多普勒速度曲线Fig.4 The Doppler velocity curves of two spectral lines, 6 569.2 and 6 562.8 Å , calculated from the reconstructed spectrogram with three different PCA orders

表3

Table 3

表3(Table 3)

表3 多普勒速度测量精度 Table 3 Accuracy of Doppler velocity measurement 波段 /Å 668阶 /(m· s-1) 100阶 /(m· s-1) 30阶 /(m· s-1) 6 569.2 71.5 37.4 28.6 6 562.8 133.1 118.8 116.6

表3 多普勒速度测量精度 Table 3 Accuracy of Doppler velocity measurement

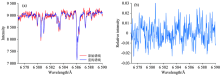
实验结果表明PCA有良好的降噪效果, 但降噪程度很大程度上都取决于阶数的选择, 越小的主成分阶数, 重构出的光谱图信噪比越高, 但阶数不应过小, 否则会丢失光谱有用信息。 对太阳光谱而言, 我们希望最大程度抑制噪声又能保留光谱主要信息, 假如噪声完全随机且PCA实现了完美降噪, 那么重构后残差图像噪声大小应等于原始图像噪声大小, 此时可以采用二阶有限差分方法定量计算各阶重构后的噪声大小, 随后寻找到合适的主成分阶数。 但是实际观测数据情况复杂, 除了随机噪声还可能存在非有用信息, 比如本组数据中时变的干涉条纹, 它会影响残差图像噪声大小的精确估计。 本实验中, 依旧按照上面依据, 采用二阶有限差分方法计算了原有数据噪声大小, 并计算残差图像的均方根差, 找到最佳阶数是74。 也可以按谱线的信噪比达到某一固定值为依据, 如本组数据, 假如以光球线6 569.2 Å 的信噪比达到100为依据, 此时最佳阶数是82。 但是从实际曲线看, 30阶以后残差图像的噪声变化趋势已变缓慢, 且主成分的贡献率也在30阶左右开始减势趋缓, 图5显示的第500行谱线轮廓中波长范围6 576~6 590 Å 这一段在PCA重构前后的变化, 图5(a)显示的是PCA重构前后的对比, 图5(b)是它们之差, 从图5(b)我们看到差异曲线呈现周期震荡性, 这体现的正是干涉条纹的特性, 表明PCA前后谱线变化最大的地方是干涉条纹得到有效剔除, 计算差异曲线的均方根差为87, 相比于原始谱线平均强度8 945.5, PCA前后谱线强度的相对变化不超过1%, 基本可认为谱线轮廓变化可以忽略, 我们也对比过重构谱线轮廓和标准谱线轮廓, 两者的差异也在1%内, 说明重构后光谱轮廓信息几乎没变。 因此, 针对本文实例, 我们认为主成分阶数取30是合适的, 在实际应用中, 主成分阶数应根据实际情况酌情选择。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 PCA前后谱线轮廓对比以及它们之差 (a): PCA重构谱线与原始谱线轮廓对比; (b): PCA重构谱线与原始谱线轮廓之差Fig.5 Comparison of the spectral line profiles between the original and reconstructed spectrogram, and their difference (a): Comparison of the spectral line profiles between the original and PCA reconstrugram; (b): The difference of the spectral line profiles between the original and PCA reconstrugted spectrogram

三维光谱数据的特征信息提取实验表明, PCA能有效的对光谱数据量进行压缩, 重构后的数据也能较好地保持原始数据信息。 同样, 数据压缩比跟主成分阶数选取有密切关系, 越小的主成分阶数, 数据压缩比越大, 但不管怎样, 应遵循最大程度保留原始数据有用信息这一准则。 尝试过基于2D-PCA的三维光谱压缩, 也比较了同样阶数下谱线轮廓残差大小, 结果显示2D-PCA方法下谱线强度的相对变化略大于1% , 这是因为在实际观测中, 观测目标的演化和望远镜跟踪误差等因素导致帧与帧间图像形态发生变化, 降低了帧间的相关系数, 从而导致特征信息提取效果不如之前方法, 这从侧面说明了特征提取效果非常依赖于用于特征分解的向量间的相关性强弱, 无论这个向量是一维形式的光谱轮廓还是二维形式的光谱图像, 只要它们存在较强相关性, PCA 技术的优越性就能得到良好体现。

针对NVST光谱数据量大以及科学目标要求和天文台站数据规范发布需求, 提出了一种基于主成分分析的太阳光谱特征信息提取和重构方法。 以光谱数据中光谱轮廓为样本向量构建二维矩阵, 通过特征分解获取特征向量和各阶主成分。 主成分重构后, 光谱数据信噪比明显提升, 谱线多普勒速度测量精度也得以明显提高, 尤其是对谱线深度较浅的光球线, 另一方面, 通过对三维光谱数据特征信息提取, 实现了数据存储和传输量大幅压缩, 简化了数据形式, 这为当前NVST光谱数据的存储和网上规范发布指明了技术路线。 本文提出的光谱信息提取方法可为中国各天文台站太阳光谱数据处理提供借鉴, 也为正在研制的光纤阵列太阳望远镜^[11](fiber arrayed solar optical telescope, FASOT)和未来中国巨型太阳望远镜^[12](Chinese giant solar telescope, CGST)海量光谱数据处理提供参考。

致谢: 感谢NVST观测组和天文技术实验室老师们提供的帮助。