作者简介: 吴明磊, 1986年生, 山东大学(威海)机电与信息工程学院博士研究生 e-mail: wuming8511@126.com
恒星的连续谱是由于黑体辐射导致的光辐射强度随波长(频率)连续光滑变化的光谱。 每条观测到的光谱数据中都会包含连续谱、 谱线和噪声。 恒星的分类主要是依据光谱的谱线、 连续谱的相对强度以及光谱的其他特征。 恒星连续谱的分布以及谱线的轮廓是由恒星大气内的物理因素决定的, 也可以根据连续谱及谱线对恒星大气的物理参数进行估计。 因而处理光谱的主要问题就是提取连续谱, 并且通过归一化进行谱线的提取。 恒星连续谱提取的算法主要有多项式逼近、 中值滤波、 形态滤波以及小波滤波等, 但是这些方法对于低质量光谱处理的鲁棒性不是很好, 因此有必要研究一种新的算法对低质量光谱的连续谱进行提取。 在仔细分析恒星低质量连续谱的基础上, 提出一种基于蒙特卡罗方法的低质量恒星连续谱拟合方法。 该方法对恒星光谱筛选过程中不在范围内的点利用蒙特卡罗均匀分布进行自动插值, 让每一个波长都对应一个流量点, 然后对这些流量点进行低阶多项式迭代拟合, 从而得到连续谱。 为了验证算法对不同信噪比的低质量光谱连续谱提取的鲁棒性, 利用不同的信噪比在原始光谱中加入不同的高斯白噪声对低质量光谱进行模拟。 结果表明蒙特卡罗算法对不同信噪比的低质量光谱的拟合具有较高的精度与较强的鲁棒性。
The stellar continuum is a sort of spectrum whose light intensity changes continuously and smoothly with wavelength (frequency) due to blackbody radiation. Each observed spectrum contains continuous spectra, spectral lines and noises. The classification of stellar is mainly based on the spectral lines of the spectrum, relative intensity of the continuum and other characteristics of the spectrum. The distribution of the stellar continuum and the contour of the lines are determined by the stellar atmospheric parameter, so the stellar atmospheric parameter can be estimated from the continuum and the spectral lines. Therefore, the main problem of the spectral data processing is to extract the continuum and the lines. The current algorithms for stellar continuous spectral extraction are mainly polynomial approximation, median filtering, morphological filtering and wavelet filtering. However, these methods for the robustness of low-quality spectral processing are not very satisfying. Therefore, it is necessary to study a new algorithm for extracting the continuous spectrum from the low-quality spectra. In this paper, a fitting method for low-quality stellar spectrum based on Monte Carlo is proposed after careful analyses of low-quality stellar continuum. The method is used to automatically interpolate at the point where the spectrum is not in the range of the star spectrum with Monte Carlo, so each wavelength corresponds to a flow point, and then the low-order polynomial iterations are fitted to these flow points for obtaining the continuous spectrum. In order to verify the robustness of the algorithm for low-quality spectral continuum extraction with different SNRs, we use different SNRs to simulate different low-quality spectrum by adding different Gaussian white noise to the original spectrum. The result shows that the proposed algorithm has high accuracy and robustness to the fitting of low-quality spectrum with different SNRs.
由于望远镜各方面性能的提高, 使得天文学有了飞速的发展, 人类对宇宙的认识随之有了很大的提高。 国外的斯隆巡天项目(SDSS)和我国的LAMOST等大规模的巡天项目都可以从宇宙中观测到巨量的恒星光谱数据。 SDSS是目前为止最有影响力的光谱巡天项目之一[1]。 它的光谱获取能力很强, 利用2.5 m望远镜以及两个特殊的仪器, 每次曝光都可以获取600多个目标。 郭守敬望远镜[2](LAMOST)是我国2008年建成的大科学工程项目之一, 在第一年发布的2 204 860条光谱数据中达到质量标准的光谱数据只占到了不到50%。 截止到2015年6月, 先导巡天的3年正式巡天过程中, 信噪比小于10的低质量光谱也占到了15%左右[3]。 低质量光谱的主要特征是噪声大、 局部信噪比低、 连续谱异常以及谱线特征不明显等, 但是这些低质量光谱中存在着很多稀有天体、 未知天体等有价值的数据。 因此, 有必要对观测到的低质量光谱进行进一步的处理和数据挖掘。
恒星光谱主要由连续谱、 谱线和噪声组成。 通过谱线可以辨识恒星的化学成分和物理状态, 对光谱的后续研究有着重要的意义。 因此, 如何从原始光谱中提取谱线是我们进行恒星光谱研究的重要步骤。 将连续谱进行归一化是目前消除光谱中连续谱信息提取谱线的有效方法。
消除连续谱首先要进行连续谱的拟合。 目前连续谱拟合的主要方法有: 小波滤波、 中值滤波、 形态滤波以及多项式逼近等。 多项式逼近的方法实际就是多项式拟合。 多项式拟合比较简单, 所以本工作采用多项式拟合的方法[4]。 多项式拟合一般指的是用多项式函数逼近一个函数。 一般我们采用的是最小二乘法, 它通过最小化误差的平方和寻找数据的最佳函数匹配。 多项式拟合的主要问题就是基向量的选择, 基向量选择的好坏对最终的拟合光谱有着决定性影响。 在光谱拟合中的基向量指的是流量点[5]。 传统的多项式拟合的基向量(流量点)的选取主要是对部分点进行选取[4], 部分点的光谱多项式拟合特别是低质量光谱的拟合可能会造成信息失真。
针对上述问题, 提出了利用蒙特卡罗随机取点的方法, 能够对我们缺失的流量点进行模拟, 使得拟合出来的连续谱具有良好的精度和稳定性。
蒙特卡罗法(Monte Carlo method)是一种以统计学为基础建立起来的方法。 首先建立一个与问题相关的统计模型, 模型建立的准则是使所求问题的解正好是所建模型的数学期望或其他特征量; 其次通过多次试验统计出求解问题的发生概率, 利用第一步建立的统计模型, 求出所需要的参数; 再次对模拟结果进行分析总结, 验证系统的某些特性[7]。
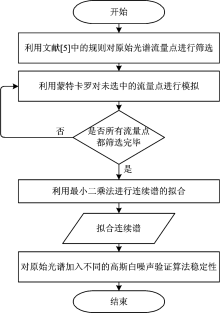
理论上讲, 只要选择适当的流量点就可以对原始光谱的连续谱进行有效的拟合。 但由于光谱的流量点并不是都符合我们的标准, 只能选取其中的某些符合条件的流量点进行拟合。 蒙特卡罗随机算法在光谱处理上的应用[6]给处理上述问题提供了新的方法。 首先利用文献[5]中的规则和蒙特卡罗算法对流量点进行筛选, 其次利用最小二乘法对连续谱进行拟合, 最后向原始光谱中加入不同信噪比验证算法稳定性。
将一条恒星光谱划分为若干个等宽的统计窗口, 在每一个窗口内根据上下限筛选出一定比例的流量点, 然后对未选中的点利用蒙特卡罗进行模拟, 模拟的步骤如下:
(1) 根据上下限(L, U), 对原始光谱点以统计窗为区间进行逐个筛选;
(2) 对未选取到的流量点利用蒙特卡罗在一定区间内进行模拟, 区间的间距就是D=U-L;
(3) 调用蒙特卡罗随机数发生器, 利用模拟的均匀分布在区间内产生随机数[8, 9]
(4) 对每一个窗口重复第二步, 直至重复的次数已达预定值;
(5) 对所有的随机数求平均值, 将这个平均值作为模拟的流量点值。
其中关于L和U指的是我们流量点的上下限, 它们的选取我们采用文献[5]中的规则, 上下限公式为
对第一步获取的流量点进行低阶多项式拟合得到连续谱, 然后对连续谱进行多次迭代的归一化, 实现归一化拟合的优化。 设波长为W, 对应的流量为F, 波长的集合为WS, 对应的流量集合为FS, 其步骤如下:
(1)对波长WS和流量FS进行5阶多项式拟合, 利用最小二乘法得到连续谱FC, 然后对连续谱进行归一化Fn=FS/FC。
(2)对归一化的光谱进行异常点的剔除, 去掉[m-3s, m+3s]范围外的点, 其中m与s分别为FC的均值和标准差。
(3)重复步骤(1)和(2), 直到没有可去除的点为止[5]。
利用不同信噪比在原始光谱里面加入高斯白噪声模拟出低质量光谱, 利用本方法对低质量光谱进行拟合, 步骤如下:
(1) 对原始光谱的流量点进行插值;
(2) 产生均值为0, 标准差为1的正态分布随机数;
(3) 对第2步的随机数进行标准化
(4) 与第3步的随机数进行结合, 产生具有一定信噪比的噪声
(5) 产生服从N(f, y)正态分布的噪声
(6) 利用不同信噪比(文中选取SNR=1: 15)对第1步到第5步进行循环。
如图2所示, 从SDSS光谱中随机抽选出了各种类型的光谱数据(M型除外, M型具有大量的分子吸收带)共1 426条进行了拟合。 图中左侧蓝色实线为原始光谱; 图中右侧红色实线为归一化光谱。 从图中可以看出本方法得出的光谱的归一化程度比较高, 对光谱进行了一个较好的拟合。
如图3所示, 图中选取图1中A类相对应的光谱依次加入信噪比(SNR)为1到5的高斯白噪声, 对低质量光谱进行模拟, 图中: 黑色代表原始光谱, 蓝色代表SNR=1, 绿色代表SNR=2, 红色代表SNR=3, 蓝绿代表SNR=4, 紫红代表SNR=5; 第一行和第三行代表不同信噪比的原始光谱, 第二行和第四行代表拟合的连续谱。
如图4所示, 图中选取了图1中相对应的各种类型的光谱, 利用本方法对原始光谱依次加入信噪比(SNR)为1到15的高斯白噪声, 对低质量光谱进行模拟。 从图中可以看出本方法对于A, B, O类的所有信噪比较低的低质量光谱的连续谱拟合有着很好的稳定性; 对于F, G和K类光谱在SNR为1到5的时候有一定的波动, 但是当SNR> 5之后也具有很好的稳定性。
为了提高低质量连续谱拟合的精度和稳定性, 在国内外研究成果的基础上提出了利用蒙特卡罗模拟的方法对筛选缺失的流量点进行了随机模拟, 然后通过多项式逼近的方法对连续谱进行了拟合, 并且通过随机选取SDSS恒星光谱数据进行了验证。 结果表明本方法有较高的精度和较好的稳定性, 对于大规模处理低质量光谱有着独特的优越性。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|