引用本文
刘智超, 张丽娟, 杨进华, 王高. 折射率调制矩阵的Bragg光栅光谱分布特性研究. 光谱学与光谱分析, 2018,38(12): 3718-3723
LIU Zhi-chao, ZHANG Li-juan, YANG Jin-hua, WANG Gao. Research on Bragg Spectral Distribution Based on Refractive Index Modulation Matrix. Spectroscopy and Spectral Analysis, 2018,38(12): 3718-3723.  
Doi: 10.3964/j.issn.1000-0593(2018)12-3718-06
Permissions
Copyright©2018, 光谱学与光谱分析
光谱学与光谱分析 所有
折射率调制矩阵的Bragg光栅光谱分布特性研究
刘智超1,2, 张丽娟3, 杨进华1, 王高4
1. 长春理工大学光电工程学院, 光电测控与光信息传输技术教育部重点实验室, 吉林 长春 130000
2. 长春理工大学光电工程学院, 光电工程国家级实验教学示范中心, 吉林 长春 130000
3. 长春工业大学计算机科学与工程学院, 吉林 长春 130012
4. 中北大学, 仪器科学与动态测试教育部重点实验室, 山西 太原 030051

作者简介: 刘智超, 1984年生, 长春理工大学光电工程学院博士研究生 e-mail:s20070384@163.com

收稿日期: 2018-01-04 接受日期: 2018-04-16
基金项目: 国家自然科学基金项目(61703056), 高等学校学科创新引智计划(111计划), 光电工程国家级实验教学示范中心资助
摘要

为了实现对光纤光栅回波光谱分布的控制, 利用传输矩阵法构建了分段调制折射率的数学模型。 通过在各个分段中以不同形式的折射率调制组合实现对回波光谱分布的控制, 研究了基于不同折射率分布条件下的谱形特性, 为实现获取任意形态的Bragg光谱分布提供了理论支撑。 系统结合耦合模理论与矩阵传输算法, 当分段后子光纤光栅尺寸符合边界条件时, 即仍可应用耦合模理论计算, 同时又可以将多段的耦合方程以正、 反向模式的形式通过矩阵函数进行表达。 由此可知, 虽然任意折射率调制组合构成的整个光纤光栅不具备通解形式, 但分段后的子光纤光栅具有可解析的特性, 同时再利用矩阵传输算法可以将m段子光纤光栅的正反向模式进行计算, 就能将任意形式光纤光栅的折射率调制函数转化为传输矩阵组, 再对其反射率分布场进行解析。 最终, 可以得到整个光纤光栅的等效正、 反模式, 即实现回波光谱分布的控制。 由理论部分可知, 回波光谱分布特性主要受正反向导模耦合系数、 纤芯位置、 分段数决定, 可由σ˙( z)和 k( z)表示。 通过MATLAB仿真分析可知, 两参数在(0, 1)范围内对反射率函数具有明显的调制作用。 随着控制参数阶数的增大, 反射率调制斜率也会增大; 当 k⊆(0.38, 0.48),σ˙⊆(0.52, 0.58)时, 反射率调制符合单调特性。 从而得到了不同控制参数条件下反射率函数的分布变化, 讨论了耦合系数对回波谱形控制的量化效果。 实验利用AVESTA公司的Ti: Sapphire飞秒激光器完成了四种不同结构光纤光栅的制作, 采用了四种折射率分段调制的FBG结构, 分别是: ①在 m段中 Λ1和 Λ2交替均匀分布; ②在 m/2段中 Λ1和 Λ2交替均匀分布, 其余段随机分布; ③在 m/2段中 Λ1和 Λ2随机分布, 其余段也随机分布; ④在整个光纤光栅段折射率随机分布。 对以上四种FBG的回波光谱分布进行测试与比较, 可知采用分段折射率调制对Bragg光谱特性的作用效果。 实验结果显示: 当以矩阵组形式的FBG若在 m段分布时, 则与传统串联型均匀FBG测试效果一致, 具有两个明显的Bragg特征峰; 而矩阵组在 m/2段中分布时, 测试光谱仍能明显获取折射率调制特征信息, 即存在两个Bragg特征峰, 但峰峰值减小, 噪声谱增大, 半宽变窄。 同时, 相比交替模式而言, 随机分布形式此种变化趋势更为明显。 由此可见, 通过控制矩阵组分布对回波谱形中特征峰值、 半宽及功率谱进行调制。 该方法在预先设计折射率调制矩阵的条件下, 可以对Bragg光谱分布进行精确控制, 实现目标回波谱形的获取。

关键词: 光纤光栅; 光谱分布; 传输矩阵组; 折射率调制
中图分类号:TN253 文献标识码:A
Research on Bragg Spectral Distribution Based on Refractive Index Modulation Matrix
LIU Zhi-chao1,2, ZHANG Li-juan3, YANG Jin-hua1, WANG Gao4
1. Key Laboratory of Optoelectric Measurement and Optical Information Transmission Technology of Ministry of Education, School of Opto-Electronic Engineering, Changchun University of Science and Technology, Changchun 130000, China
2. National Demonstration Center for Experimental Opto-Electronic Engineering Education, School of Opto-Electronic Engineering, Changchun University of Science and Technology, Changchun 130000, China
3. College of Computer Science and Engineering, Changchun University of Technology, Changchun 130012, China
4. National Key Laboratory for Electronic Measurement Technology, North University of China, Taiyuan 030051, China
Abstract

According to the form of its engraved grid, FBG sensor can be divided into uniform type, chirp type and so on. The spectrum distributions of FBG are different for different grid forms. At present, it has been reported that existing structural parameters were mainly analyzed by the literature. The functional model was studied for obtaining the spectral distribution, which can be from any kind of FBG, and its parameter design was realized. In order to realize the control of the echo spectrum distribution by FBG, a mathematical model of the segmented modulation index was established by using transfer matrix method. The spectrum distribution of the echo was controlled by the combination of different refractive index modulations in each segment, and the spectral characteristics under different refractive index distributions were studied. It provided theoretical support for obtaining the Bragg spectrum distribution in any form. In the system, coupled-mode theory and matrix transmission algorithms were used in combination. Compared with the traditional uniform FBG, σ and k were no longer constants, but rather σ( z) and k( z) as a function of form, so for any FBG structure did not have an analytic solution. However, if the FBG was divided into m sections, m sub-FBGs could be obtained from the concrete σ( z) and k( z) functions on each small section, so that the overall effects of the FBG could be obtained by the matrix transmission method. The FBG was divided into m small sections in the z-axis direction, and m sub-FBGs could be obtained from the specific σ( z) and k( z) functions in each small section, so that the overall effects of the FBG can be obtained by the matrix transmission method. When the size of sub-FBG segmented meets the boundary conditions, the coupling mode theory can still be applied. At the same time, it can express the multi-section coupled equations through the matrix function in the form of positive and negative modes. It can be seen from this that the entire FBG composed of arbitrary refractive index modulation does not have the generalized form, but it can be resolvable for the segmented sub-FBGs. And the matrix transmission algorithm can be used to calculate the positive and negative modes of the m-segment sub-FBGs. So the refractive index modulation function of any type of FBG can be transformed into a transmission matrix group. The reflectivity distribution field can also be analyzed. Finally, the equivalent positive and negative modes of the whole FBG can be obtained, so as to realize the control of the echo spectrum distribution. As can be seen from the theoretical part, the spectrum distribution characteristics of echo are mainly determined by the coupling coefficients of the forward and reverse guided modes, the position of the core and the number of segments. They can be represented by σ( z) and k( z). Through MATLAB simulation analysis showed that the two parameters have significant modulation effects on the reflectivity function in the range of (0,1). As the order of control parameters increases, the slope of reflectivity modulation will also increase. In case of k⊆(0.38, 0.48), σ⊆(0.52, 0.58), it is monotonically tuned for reflectivity modulation. The distribution of the reflectivity function under different control parameters was obtained. The quantitative effects of the coupling coefficient on the control of the echo spectrum were discussed. Taking two specific pitch Λ1 and Λ2 as an example, after splitting the whole FBG into m sub FBGs, Λ1 and Λ2 were placed on different sub-sections. The spectrum distribution patterns of FBG were analyzed according to different grid layouts. If the spectrum characteristics of FBG change by the parameters and distribution forms of Λ1 and Λ2, and they are resolvable, the Bragg spectral characteristics can be considered as controllability. Through the parameter control any spectrum distribution can be achieved. In the experiment, AVESTA’s Ti: Sapphire femtosecond laser (Its center wavelength 800 nm, frequency 1 kHz, peak pulse energy 800 nJ.) was used to fabricate four different structured fiber gratings. Four kinds of refractive index modulation FBG segment structure were employed. Respectively: (1) Λ1 and Λ2 were evenly distributed alternately in the m section; (2) Λ1 and Λ2 were evenly distributed alternately in the m/2 section, and the rest of section were randomly distributed; (3) Λ1 and Λ2 were randomly distributed in the m/2 section, and the rest of section were randomly distributed, too; (4) The refractive index of the entire fiber grating segment was randomly distributed. Echo spectrum distribution of the above four FBGs was tested and compared, so the spectrum properties of Bragg was studied by the segmented refractive index modulation. The experimental results showed that when the FBGs in the form of matrix group are distributed in the m section, they are consistent with the traditional series homogeneous FBG test and have two obvious Bragg characteristic peaks, and they are located at 1 551.485 and 1 563.572 nm, respectively, and have a high signal-to-noise ratio. It is consistent with the test results of two series-connected FBGs with fixed pitch and is also a special solution to the piecewise modulated function. In case 2, its characteristic peak positions are 1 551.499 and 1 563.551 nm, its absolute error is better than 0.030 nm. Its half-width is better than that of case 1, but its noise power increases greatly and the signal-to-noise ratio decreases. In case 3, the absolute error of the characteristic peak position is better than 0.050 nm, and the sharpness of the characteristic peak is further increased, and the noise power is further increased, and the signal-to-noise ratio is the worst. When the matrix group is distributed in the m/2 segment, the refractive index modulation characteristic information can still be obtained obviously in the test spectrum, that is, there are two Bragg characteristic peaks, but the peak-peak value decreases, and the noise spectrum increases, and the half-width narrows. At the same time, the trend of stochastic distribution is more obvious than that of alternation. Thus, the characteristic peak, half-width and power spectrum in the echo spectrum can be modulated by controlling the matrix group distribution. The method can accurately control the Bragg spectrum distribution under the pre-designed refractive index modulation matrix to obtain the target echo spectrum.

Key words: Fiber grating; Spectrum distribution; Transmission matrix group; Refractive index modulation
引 言

光纤传感技术是以光纤作为传感器与传输介质的传感网络[1]。 其灵敏度高、 测试范围广、 抗干扰能力强, 对微弱信号具有很好地检测能力[2], 同时还适用于野外工作环境, 在合适保护下可以长时间服役[3]。

从光纤光栅工作原理出发, 主要分为瑞利散射型、 布里渊散射型、 拉曼散射型、 布拉格反射型等[4, 5, 6, 7]。 瑞利散射型主要是通过光在介质中相位变化及其光频域变化实现对待测量分析[8]; 布里渊散射型又分为时域型和干涉型两种, 通过监测布里渊散射量实现对待测量的反演[9]; 拉曼散射型与瑞利散射型的测试方法相近, 主要区别在于对测试贡献的频率不同, 由其不同的能级所决定。 布拉格反射型就是光纤布拉格光栅[10, 11, 12](fiber Bragg grating, FBG), 其利用回波信号包含FBG位置上物理信息的特性。 FBG根据不同的折射率调制形式构成了均匀型、 相移型、 啁啾型等[13], 现有的各种形式都是基于具有明确调制规律的FBG结构设计的, 而本研究是针对一种更具通用模式的折射率调制形式, 并利用耦合模理论及矩阵传输算法实现新型FBG的分析及测试。

1 矩阵传输模型

重点讨论单模少模条件下的光纤波导过程, 主要分析正向与反向模式的耦合问题[14], 也就是低阶模条件下的耦合形式计算与分析。 当针对正向模式与反向模式时, 光纤中电磁波可表示为

E→=∑AμE→μ(x, y)e-j(ωt-βμz)+∑BμE→μ(x, y)ej(ωt-βμz)(1)

其中, Aμ 是正向模式振幅量, Bμ 是反向模式振幅量, t是时间, ω 是频率, β μ 是相移量, z是光纤上的某一位置, x和y是垂面上的坐标值。

对于微米级光纤光栅而言, 它的模间耦合主要体现在正向模式与反向模式的耦合[15], 所以令纤芯自由模的狄拉克(δ )函数为δ =δ 01-01, 光纤正反向耦合系数为σ =k01-01, 条纹可见度为m, k=mσ /2, σ˙=σ +δ , 则有+z方向对应的振幅R和-z方向对应的振幅S, 化简式(1)后可得

dR/dz=jσ˙R+jkS, dS/dz=-jσ˙S-jkR(2)

与式(2)匹配的边界条件有R(0)=1, S(L)=0。 对于传统光纤光栅 σ˙和k是固定值, 所以回波光谱中特征峰位置是固定值; 但本系统采用的分段折射率调制使其发生明显的改变, 即 σ˙和k是函数, 可表示为 σ˙(z)和k(z), 所以系统的回波光谱是变化的, 是可以根据系统的参数设置而调整的, 则其反射系数可表示为

ρ(z)=-k(z)sinhk2(z)-σ˙2(z)Lσ˙(z)sinhk2(z)-σ˙2(z)L+jk2(z)-σ˙2(z)coshk2(z)-σ˙2(z)L(3)

虽然对于任意FBG的折射率调制并没用完备的解析形式, 但通过分段求解的方法可以将多个子FBG的传输矩阵求解出来, 然后再将多个子FBG的正向模式与反向模式相累加, 从而获得整个FBG的最终表达形式。 假设在z轴上FBG被分为m段, 它的有效长度是L, 则第i段可表示为Li, 它的反向模式是Ri-1, Si-1, 正向模式是Ri+1, Si+1, 则其传输矩阵Ti有

Ti=cosh(γBLi)-jσ˙/γBsinh(γBLi)-jσ˙/γBsinh(γBLi)jσ˙/γBsinh(γBLi)cosh(γBLi)+jσ˙/γBsinh(γBLi)(4)

故FBG综合传输矩阵有

RmSm=T1·T2…Ti…TmR0S0=TR0S0(5)

相比之下传统FBG固定折射率调制传输矩阵计算过程中多个参量被简化掉, 最终的输出表达仅体现波长、 调制系数等信息, 所以存在反射系数和反射波长的通解形式。 而本工作采用分段折射率调制就不能一次性获得整个FBG的通解形式, 只能通过分段求解再将每段的正向模式与反向模式相叠加的方法实现, 由此可以利用 σ˙(z)和k(z)两组函数完成对回波光谱特征峰位置、 峰峰值、 半宽及噪声谱的控制。

2 仿真计算

首先, 将整个FBG分为m段, 对每个子FBG进行耦合模求解。 然后, 通过传输矩阵法将各个子FBG的模式相乘, 获得系统的最终函数形式。 最终, 完成对特征波长位置、 振幅等的控制。 对不同 σ˙(z)和k(z)进行分析计算, 验证了FBG回波谱形与各个参数之间的变化关系。 设光纤纤芯的折射率是1.457, 包层的折射率是1.448, 光纤直径6.50 μ m, 包层直径125.0 μ m, 有效光栅长度是10.0 mm, 子FBG分段数2 000份。

测试条件分别是: (1) σ˙(z)=0.5, k(z)=a× z; (2) σ˙(z)=a× z, k(z)=0.5; (3) σ˙(z)=a× z, k(z)=b× z; (4) σ˙(z)=a× z2, k(z)=b× z2。 为了仿真数据能更好地体现参数变化造成的反射系数变化, 所以上式中的常数参数均采用1代替, 即a=b=1, 结果如图1所示。

图1 不同 σ˙(z)和k(z)条件下的反射函数
(a): σ˙(z)=0.5, k(z)=a× z; (b): σ˙(z)=a× z, k(z)=0.5Fig.1 Reflectivity functions of different σ˙(z) and k(z)

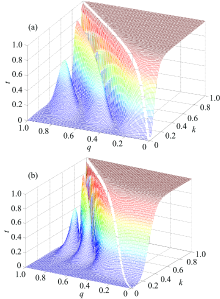
图1(a)和(b)表示对低阶参数变化的仿真分析结果, 当 σ˙(z)=0.5, k(z)=az时, 分别为一个常数和一个线性函数, 由此可以得到FBG反射系数的函数变化规律, 系统对 σ˙(z)和k(z)的调节可以是相应位置上的反射系数改变, 从而调制回波光谱的主要参数。 图1(a)中, 在(0, 0.4)之间反射系数存在区间极大值, ρ =0.256, 这个极值在控制反射振幅具有明显的选择作用; 在(0.4, 0.5)之间, 反射系数单调递增, 可以大幅提升回波光谱的振幅量。 图1(b)中, 在(0.6, 1)之间反射系数存在两个极大值, ρ 1=0.521和ρ 2=0.294, 不同的极值峰值可以用于回波光谱不同位置峰峰值的控制; 在(0.5, 0.6)之间, 反射系数单调递减, 可以用于控制回波光谱的振幅量。

图2(a)为两个参数均采用线性函数控制的情况, 可以看出当两个参数均为函数时, 反射系数函数分布明显复杂了, 变成了三维曲面结构。 其总体趋势是在整个调制区间存在两个极值峰位置, 峰值位置受两个参数综合分布的影响; 图2(b)为两个参数均为二次型函数的情况, 虽然反射系数的三维曲面分布仍存在两个极值峰, 但可以看出曲面的斜率发生了明显变化, 斜率大幅增加, 这说明当参数的阶数提高时, 反射系数曲面的斜率会随之增大, 也就是当提高控制参数的阶数时可以更快地调节回波光谱的扫描速度。

图2 不同 σ˙(z)和k(z)下的反射率函数
(a): σ˙(z)=a× z, k(z)=b× z; (b): σ˙(z)=a× z2, k(z)=b× z2Fig.2 Reflectivity functions of different σ˙(z) and k(z)

3 验证性实验
3.1 实验条件

实验制作了四种不同折射率调制结构的FBG对提出的分段调制设想进行验证, 分析其对回波光谱的控制作用。 目标光谱为两个特征峰和一组随机光谱; 第一个目标光谱用于分析两个特征峰对回波光谱峰峰值位置的控制能力及对特征峰峰值高度、 半宽的控制能力; 第二个目标光谱用于分析随机折射率调制对噪声谱的控制能力。 采用AVESTA公司Ti:SAPPHIRE飞秒激光器制作FBG, 其中心波长0.80 μ m, 峰值脉冲为1.0 MJ。 由此对四种不同FBG进行测试, 假设刻制的固定栅距分别为Λ 1和Λ 2, 四种FBG的折射率调制方法分别是: (1) 在整个m段中, 由Λ 1和Λ 2间隔刻制, 由此形成两组栅距一定的混合栅格; (2) 在整个m段中, m/2段由Λ 1和Λ 2间隔刻制, 另m/2段由随机栅构成, 调制栅为均匀分布; (3) 在整个m段中, m/2段由Λ 1和Λ 2间隔刻制, 另m/2段由随机栅构成, 调制栅为随机分布; (4) 在整个m段中, 折射率随机分布。

3.2 结果分析与讨论

实验结果如图3所示。

图3 四种FBGs的光谱分布Fig.3 The spectra of four kinds of FBGs

图3(a)表示第(1)种情况的回波光谱, 反射光谱中存在两个较大的特征峰, 其位置分别在1551.485和1563.572 nm处, 与两个明显峰峰值的设计要求相符, 同时可以看出两个峰峰值的信噪比较好, 噪声波动较小。 其结构可以理解为两个具有固定栅距FBG的串联, 由于是固定栅距, 所以采用耦合模理论可以直接得到其通解形式, 其回波光谱也是比较明显的。 图3(b)表示第(2)种情况的回波光谱, 其特征峰在1 551.499和1 563.551 nm处, 中心波长位置并没有因为随机折射率调制的引入而发生改变, 但其半宽相对变小, 峰峰值锐度提高, 噪声功率也随之增大, 信噪比随之降低; 图3(c)表示第(3)种情况的回波光谱, 特征峰位置依旧保持不变, 波峰锐度进一步增大, 噪声功率也变大了, 信噪比在这几组测试中最低; 图3(d)表示第(4)种情况的回波光谱, 回波光谱为随机分布的形式, 与其折射率随机调制的形式相符。 总之, 系统可以通过构造不同的m段子FBG实现对回波光谱的有效控制。 图3(b)和(c)说明了参数对回波光谱控制的可行性, 即在整个FBG上没有解析性但仍能够通过子FBG实现对光谱的调制。 最终, 对比图3(b), (c)和(d)可知, 随机折射率的分布控制对于回波光谱同样具有影响, 主要体现在对噪声功率谱的控制上。

4 结 论

研究了一种基于折射率调制矩阵的光谱控制方法, 通过对折射率进行分段调制实现了对回波光谱的控制。 利用耦合模算法及矩阵传输的特点完成了回波光谱与分段调制的模型构建。 实验针对四种折射率调制结构的FBG进行分析, 分析了 σ˙(z)和k(z)两个参数对回波光谱的控制能力。 由此说明了采用分段折射率调制的方法可以对回波光谱特征峰位置、 半宽以及噪声谱进行控制, 论证了系统的可行性。

The authors have declared that no competing interests exist.

参考文献
[1] García-Miquel H, Barrera D, Amat R, et al. Measurement, 2016, 80: 201. [本文引用:1]
[2] June J, Nam H, Lee J H, et al. Appl. Opt. , 1999, 38(1): 2749. [本文引用:1]
[3] Khan M M, Panwar N, Dhawan R. Sensors & Actuators A Physical, 2014, 205(205): 79. [本文引用:1]
[4] Li J, Sun B. High Power Laser & Particle Beams, 2015, 27(2): 641. [本文引用:1]
[5] Ferreira L A, Araujo F M, Santos Jose L, et al. Opt. Eng. , 2000, 39(8): 2226. [本文引用:1]
[6] Sumayyah M I, Mohammed R H A, Aiman I, et al. Microwave Opt. Technol. Lett. , 2012, 54(11): 2447. [本文引用:1]
[7] Spirin V V, Shlyagin M G, Miridonǒ S V, et al. Optics and Laser in Engineering, 2000, 32(5): 497. [本文引用:1]
[8] LIU Zhi-chao, YANG Jin-hua, ZHANG Liu, et al(刘智超, 杨进华, 张刘, 等). Spectroscopy and Spectral Analysis(光谱学与光谱分析), 2016, 36(10): 3377. [本文引用:1]
[9] LIU Yan, LI Yang, YAN Xiao-jun, et al(刘艳, 李阳, 闫小军, 等). J. Infrared Millim. Waves(红外与毫米波学报), 2016, 35(1): 72. [本文引用:1]
[10] Li Yang, Lu Ping, Bao Xiaoyi, et al. Optics Letters, 2014, 39(8): 2294. [本文引用:1]
[11] LI Zhi-zhong, XU Zhong-liang, LI Hai-tao(李智忠, 许忠良, 李海涛). Acta Photonica Sinica(光子学报), 2014, 43(6): 0606004-1. [本文引用:1]
[12] WANG Gui-na, CENG Jie, MU Hao, et al(王桂娜, 曾捷, 穆昊, 等). Lsaer & Infrared, 2015, 45(1): 66. [本文引用:1]
[13] Lizarraga N, Puente N P, Chaikina E I, et al. Opt Express, 2009, 17(2): 395. [本文引用:1]
[14] Li J Z, Sun B C. High Power Laser & Particle Beams, 2015, 27(2): 641. [本文引用:1]
[15] Khan M M, Panwar N, Dhawan R. Sensors & Actuators A Physical, 2014, 205(205): 79. [本文引用:1]