基于分数阶微分算法的大豆冠层氮素含量估测研究

引用本文

张亚坤, 罗斌, 潘大宇, 宋鹏, 路文超, 王成, 赵春江. 基于分数阶微分算法的大豆冠层氮素含量估测研究[J]. 光谱学与光谱分析, 2018,38(10): 3221-3230.
ZHANG Ya-kun, LUO Bin, PAN Da-yu, SONG Peng, LU Wen-chao, WANG Cheng, ZHAO Chun-jiang. Estimation of Canopy Nitrogen Content of Soybean Crops Based on Fractional Differential Algorithm[J]. Spectroscopy and Spectral Analysis, 2018,38(10): 3221-3230.
Doi:10.3964/j.issn.1000-0593(2018)10-3221-10 复制到剪切板

Permissions

《光谱学与光谱分析》期刊社所有

基于分数阶微分算法的大豆冠层氮素含量估测研究

张亚坤^1,^2,³, 罗斌^2,³, 潘大宇^2,³, 宋鹏^2,³, 路文超^2,³, 王成^2,³, 赵春江^1,^2,^3,^*

1. 东北农业大学电气与信息学院, 黑龙江哈尔滨 150030

2. 北京农业智能装备技术研究中心, 北京 100097

3. 国家农业智能装备工程技术研究中心, 北京 100097

*通讯联系人 e-mail: zhaocj@nercita.org.cn

作者简介: 张亚坤, 1991年生, 东北农业大学电气与信息学院博士研究生 e-mail: zhangyakun2011@163.com

收稿日期: 2017-12-28 接受日期: 2018-04-09

基金: 国家自然科学基金项目(31601216)和北京市农林科学院创新能力建设专项(储备性研究)(KJCX20170418)资助

摘要

氮素与作物的生长发育、产量和品质密切相关。作物冠层氮素含量的快速、准确、无损检测对于作物营养诊断和长势评估具有重要意义。传统的氮素检测方法检测周期长、操作复杂, 同时具有破坏性, 无法实现作物氮素含量在时间和空间上的连续动态监测。基于光谱遥感技术快速、无损地获取作物氮素含量是近年来作物组分快速检测研究的热点。当前的研究大多基于原始光谱或整数阶微分(一阶、二阶)预处理后的光谱进行氮素含量预测, 原始光谱或整数阶微分预处理后的光谱会忽略光谱曲线间的渐变信息, 影响氮素含量的预测准确度。与原始光谱和整数阶微分方法相比, 分数阶微分算法在背景噪声去除、有效信息提取等方面较有优势。为研究分数阶微分预处理算法在作物氮素检测中的应用, 本文以不同施肥处理下的盆栽大豆作物为研究对象, 获取大豆苗期、花期、结荚期和鼓粒期四个生育期共256组冠层高光谱及对应的大豆冠层氮素含量(CNC)数据, 运用分数阶微分算法对光谱数据进行0~2阶微分预处理, 微分间隔为0.1, 分别采用归一化光谱植被指数NDSI、比值光谱指数RSI对预处理后的光谱数据和大豆冠层氮素含量数据进行相关性分析, 得到各阶微分预处理下NDSI α( α代表分数阶微分阶数)与大豆CNC, RSI α与大豆CNC相关系数绝对值的最大值及其对应的波段组合——最优波段组合NDSI α(opt)和RSI α(opt), 采用线性回归方法, 建立各阶微分下NDSI α(opt)与CNC, RSI α(opt)与CNC的预测模型, 并与常用植被指数(VOGII, MTCI, DCNI, NDRE)建立的氮素含量预测模型进行比较, 研究分数阶微分算法对大豆作物冠层氮素含量预测模型的效果。结果表明: (1)在0~2阶微分范围内, 最优波段组合NDSI α(opt), RSI α(opt)与大豆CNC的相关系数随阶数增加呈现先升高后下降趋势。其中, 0.8阶微分下NDSI_0.8( R₇₂₅, R₇₆₉)与大豆CNC的相关系数最大, 为0.875 9; 0.7阶微分下RSI_0.7( R₅₄₈, R₇₆₇)与大豆CNC的相关系数最大, 为0.865 1; (2)分数阶微分预处理能够细化光谱数据中的有效信息, 增强光谱数据对冠层氮素含量的敏感性, 尤其是增强红边平台波段与氮素含量的正相关性及绿波段与氮含量的负相关性; (3)与整数阶微分、常用植被指数相比, 分数阶微分能够提高大豆CNC预测模型的准确性。其中, 基于0.7阶微分RSI_0.7( R₅₄₈, R₇₆₇)建立的大豆CNC预测模型与0阶微分RSI₀( R₇₂₅, R₇₆₉)相比建模集决定系数(RC2)和预测集决定系数(RP2)分别提高了0.061 9和0.016 6, 建模集均方根误差(RMSEC)和预测集均方根误差(RMSEP)分别降低了0.552 5和0.180 9, 预测相对偏差(RPD)提高了0.110 4。基于0.7阶微分RSI_0.7( R₅₄₈, R₇₆₇)建立的大豆CNC预测模型与VOG II相比RC2和RP2分别提高了0.086 6和0.025 5, RMSEC和RMSEP分别降低了0.757 5和0.248 3, RPD提高了0.146 88; (4)基于0.7阶微分比值光谱指数RSI( R₅₄₈, R₇₆₇)建立的大豆LNC预测模型较优, 其RC2为0.748 4,RP2为0.800 3, RMSEC为4.752 9, RMSEP为3.511 1, RPD为2.253 7, 能够较好的估测大豆冠层氮素含量。研究表明分数阶微分算法在大豆冠层氮素含量的定量预测中具有一定的优势, 为光谱遥感技术在作物氮营养检测中的应用开拓了新的思路。

关键词: 冠层氮素含量; 高光谱数据; 植被指数; 分数阶微分算法

中图分类号:O657.3 文献标志码:A

Estimation of Canopy Nitrogen Content of Soybean Crops Based on Fractional Differential Algorithm

ZHANG Ya-kun^1,^2,³, LUO Bin^2,³, PAN Da-yu^2,³, SONG Peng^2,³, LU Wen-chao^2,³, WANG Cheng^2,³, ZHAO Chun-jiang^1,^2,^3,^*

1. School of Electrical and Information, Northeast Agricultural University, Harbin 150030, China

2. Beijing Research Center of Intelligent Equipment for Agriculture, Beijing 100097, China

3. National Research Center of Intelligent Equipment for Agriculture, Beijing 100097, China

*Corresponding author

Abstract

Nitrogen is one of the most important fertilizers and closely related to the growth, development, yield and quality of crops. Rapid, accurate and non-destructive assessment of nitrogen content in crops is critical for nutrition diagnosis and growth monitoring. Traditional detection methods of nitrogen content are complicated, time-consuming and destructive, which makes the continuous dynamic monitoring of nitrogen content in time and space impossible. It is a hot topic for rapid and non-destructive estimation of crop nitrogen content based on spectral remote sensing technology in recent years. Nevertheless, existing researches about the estimation of nitrogen content were mostly focused on the original or integer differential spectra (first order, second order). Some studies indicated that the original or integer differential spectra might ignore the effective information, which would influence the estimation accuracy of nitrogen content in crops. Fractional order differential algorithm has the advantages in background noise removal and effective information extraction compared with the integer differential methods. Hence, the objective of this study was to explore the feasibility of detecting nitrogen in crops by fractional order differential algorithm. 256 datasets, which were consisted of canopy spectral data and the relevant canopy nitrogen content (CNC) data, were collected during seedling, flowering, pod and drum stages in soybean plants. The plants were treated with different fertilizer components under pot conditions. 0~2 order differentials of spectral data were computed by Grünwald-Letnikov fractional differential equation with differential interval of 0.1. Afterwards, the correlation between the preprocessed spectra and soybean CNC under different fractional order differential were analyzed using the normalized difference spectral index (NDSI) and ratio spectral index (RSI). The maximums of correlation coefficient between soybean CNC and NDSI _α ( α is the fractional differential order), and between soybean CNC and RSIα were determined under each fractional order differentials. Simultaneously, the corresponding optimal band combinations of NDSI _α(opt) and RSI _α(opt) were obtained respectively. Eventually, the estimation models of soybean CNC based on NDSI _α(opt) and RSI _α(opt) under different fractional order differential were established and compared using linear regression method. The estimation models of soybean CNC based on five common vegetation indices including VOG II, MTCI, DCNI, NDRE and TCARI were also established and compared. The results showed that: (1) With the increasing of differential order, the correlation coefficients between soybean CNC and NDSI _α(opt), soybean CNC and RSI _α(opt) increased firstly and then decreased in the fractional differential range of 0~2. For NDSI _α, the maximum correlation coefficient was obtained between soybean CNC and NDSI_0.8( R₇₂₅, R₇₆₉) under 0.8 order differential, and the relevant value was 0.875 9. For RSI _α, the maximum correlation coefficient was obtained between soybean CNC and RSI_0.7 ( R₅₄₈, R₇₆₇) under 0.7 order differential, and the relevant value was 0.865 1; (2) The useful information in spectral data could be extracted and refined using fractional differential algorithm. Therefore, the sensitivity of spectra to soybean CNC could be enhanced. Specifically, the positive correlation between soybean CNC and the band near red edge platform, and the negative correlation between soybean CNC and near the band near green region were enhanced; (3) Compared with the models developed by integer differential and common vegetation indices, the estimation models based on fractional differential were more accurate. For integer differential, the determination coefficients of calibration (RC2) and prediction (RP2) based on RSI_0.7( R₅₄₈, R₇₆₇) under 0.7 order differential improved 0.061 9 and 0.016 6 compared with the model based on RSI₀ ( R₇₂₅, R₇₆₉) under 0 order differential, respectively. The relevant root mean square errors of the calibration (RMSEC) and prediction (RMSEP) were reduced 0.552 5 and 0.180 9, respectively. The relevant ratio of prediction to deviation (RPD) increased 0.110 4. For common vegetation indices, theRC2 andRP2 based on RSI_0.7( R₅₄₈, R₇₆₇) under 0.7 order differential improved 0.086 6 and 0.025 5 compared with the model based on VOG II, respectively. The relevant RMSEC and RMSEP were reduced 0.757 5 and 0.248 3, respectively. The relevant RPD increased 0.146 88; (4) The model based on the ratio spectral index RSI_0.7( R₅₄₈, R₇₆₇) under 0.7 order differential had the best performance in estimation of soybean CNC withRC2 of 0.748 4,RP2 of 0.800 3, RMSEC of 4.752 9, RMSEP of 3.511 1 and RPD of 2.253 7 in this study. The results indicated that fractional differential algorithm had the advantages in the quantitative estimation of soybean CNC, which provided a new view for the estimation of crop nitrogen content based on spectral remote sensing technology.

Keyword: Canopy nitrogen content; Hyperspectral data; Vegetation indices; Fractional order differential algorithm

文章图片

引言

氮素与作物的生长发育、产量和品质密切相关, 快速、准确地获取氮素含量是作物长势评价和施肥调控的基础^{[1, 2]}。传统的氮素检测方法主要有凯氏定氮法、碱蒸馏法、靛酚蓝比色法、杜马斯燃烧法, 这些检测方法具有检测灵敏度高、结果准确的优点, 但因检测周期长、操作复杂、同时具有破坏性, 导致无法实现作物氮素含量在时间和空间上的连续动态监测^[3]。如何快速、无损地获取作物氮素含量为作物营养评估与施肥决策提供科学依据, 是近年来作物组分快速检测研究的热点。

近年来, 光谱测量技术已成为作物营养快速、无损诊断的重要技术手段。作物光谱信息能够反映作物的生化组分、胁迫程度、病害情况等生长信息, 是生物、非生物因子共同作用的体现^[4]。目前国内外学者已开展了该技术用于作物氮素测量的相关研究。在这些研究中, 大多基于原始光谱或整数阶微分(一阶、二阶)预处理后的光谱进行氮素含量预测。 Inoue等^[5]采用一阶微分比值光谱指数准确地估测了水稻冠层氮素含量。 Miphokasap等^[6]利用甘蔗冠层一阶微分光谱数据实现了甘蔗冠层氮素含量的估测。梁亮等^[7]采用一阶微分归一化氮指数进行小麦冠层氮素含量预测。有研究采用一阶微分、二阶微分处理后的油菜叶片光谱建立了油菜叶片氮素含量的估算模型。原始光谱或整数阶微分预处理后的光谱虽然在一定程度上能够预测作物氮素含量, 但是上述光谱曲线间差异较大, 会忽略光谱曲线间的渐变信息, 进而影响预测准确度。分数阶微分是整数阶微分的推广, 相比整数阶微分, 在背景噪声去除、有效信息提取等方面更具优势, 已广泛应用于图像识别、信号处理等领域^{[8, 9, 10]}。目前, 在光谱数据处理过程中, 分数阶微分已得到越来越广泛的应用。张文文等^[11]发现分数阶微分预处理能够提高玉米冠层光谱与叶片铜含量的相关性。王敬哲等^[12]应用分数阶微分对荒漠土壤有机碳含量进行估算, 发现分数阶微分比整数阶微分具有更高的预测准确度。上述研究表明, 分数阶微分能够有效提取光谱信息中的潜在信息, 提高预测模型准确度。关于分数阶微分在作物氮素含量检测方面的研究较为少见。

本工作以大豆为研究对象, 设计不同施肥处理下的大豆作物栽培试验, 获取不同生育期大豆作物冠层高光谱数据以及对应的冠层氮素含量数据, 之后采用分数阶微分算法对获取的冠层光谱数据进行预处理, 并进一步建立大豆冠层氮素含量的预测模型, 探索分数阶微分在大豆氮营养状况检测与诊断中的应用, 尝试为作物氮营养检测开拓新的思路。

1 实验部分

1.1 试验设计

1.1.1 大豆样本

本试验于2017年4月5日至2017年8月20日在北京市昌平区国家精准农业研究示范基地进行。为了消除大田中不可控因素(降雨、高温、病害等)的影响, 试验采用温室内盆栽方式种植大豆, 大豆品种为中黄13和齐黄35。为获取有代表性样本数据, 试验依据三因素二次正交回归试验原则^[13], 采用尿素(N)、磷酸二氢钙(P)、硫酸钾(K)进行定量施肥, 每个品种设置15个肥料处理、 1个对照处理(不施肥), 两个品种共计32个处理, 每个处理下设置4次重复, 共种植128盆。在2017年5月14日(苗期)、 2017年6月7日(花期)、 2017年6月28日(结荚期)和2017年7月20日(鼓粒期)四个时间节点进行数据采集。采集时, 各处理下随机选择两盆大豆进行冠层高光谱图像数据和冠层氮素含量数据的采集, 每个生育期采集64个样本数据, 四个生育期共获取256个样本数据。

1.1.2 大豆冠层光谱图像采集

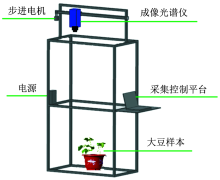
采用北京卓立汉光仪器有限公司的Image-λ -V10E-LU成像光谱仪系统进行大豆冠层高光谱成像数据采集。该成像光谱仪的光谱范围是400~1 000 nm, 光谱分辨率为2.8 nm, 视场角为25° 。试验期间天气晴朗, 数据采集时间在10:00— 14:00。采集时, 将成像光谱仪固定在扫描云台上, 距离大豆冠层1.5 m, 因此可计算出成像光谱仪的足印直径为0.665 m, 系统设置曝光时间为0.6 ms, 线性扫描速度为2.25 cm· s^-1。光谱采集系统如图1所示。

	Figure Option View Download New Window
	图1 高光谱成像采集系统示意图Fig.1 Diagram of the hyperspectral imaging acquisition system

为消除环境因素对高光谱成像数据的影响, 采用黑色吸光布隔离除大豆植株之外的背景, 使得成像光谱视场范围内只有大豆植株。在试验过程中, 同时对采集的高光谱成像数据进行了标准白板和暗电流的校正, 标准白板由聚四氟乙烯材料制成, 校正公式如式(1)

$R = \frac{I_{raw} - I_{dark}}{I_{white} - I_{dark}} (1)$

其中I_raw是大豆冠层高光谱成像原始数据, I_white是白板数据, I_dark暗电流数据, R是校正后大豆冠层高光谱成像数据。将校正后高光谱成像数据导入ENVI5.2高光谱数据处理软件中进行处理, 从而获取大豆冠层光谱信息。

1.1.3 大豆冠层氮素含量测定

在大豆冠层高光谱数据获取后, 采集大豆冠层完全展开的5片叶子, 作为一组样本, 装入标号的纸袋中, 然后将样本放入105 ℃烘箱杀青30 min, 之后在80 ℃下烘干至恒重, 粉碎后过60目不锈钢筛。最后称取0.2 g样品, 加入浓硫酸消煮后, 采用AA3连续流动分析仪进行氮素含量测定, 即大豆冠层氮素含量(canopy nitrogen content, CNC)。

1.2 数据处理及模型构建

1.2.1 有效样本选取

将试验中测得的256组氮素含量数据, 采用3倍标准差对氮素含量数据进行异常值剔除。同时结合冠层光谱曲线, 采用蒙特卡洛算法进行异常光谱数据剔除, 最终得到230个样本。将这230个样本按氮素含量由低到高排序, 按照Kennard-Stone(K-S)分类算法划分为建模集和预测集, 如表1所示。数据表明, 所选取的建模样本包含较大的氮素范围, 具有很好的代表性。

表1 大豆CNC统计结果 Table 1 Statistics values of nitrogen content in soybean leaves

1.2.2 基于分数阶微分算法的光谱数据预处理

选取有效样本后, 采用分数阶微分算法进行光谱数据预处理。目前分数阶微分主要有三种经典的定义形式, 分别是Riemann-Liouville, Grü nwald-Letnikov和Caputo定义^[14]。其中Grü nwald-Letnikov微分定义形式已在光谱数据处理和信息提取方面有广泛应用^{[8, 11, 12]}, 本文采用Grü nwald-Letnikov微分定义形式进行数据预处理, 其表达式如式(2)

$\begin{array}{l} \frac{d^{α} f (λ)}{d λ^{α}} \approx f (λ) + (- α) f (λ - 1) + \\ \frac{(- α) (- α + 1)}{2} f (λ - 2) + \dots + \frac{Γ (- α + 1)}{n! Γ (- α + 1)} f (λ - n) (2) \end{array}$

式(2)中, Γ 为Gamma函数, λ 为对应的波长点, n为微分上下限之差, α 为任意阶数。若α =0, 1和2时, 分别表示原函数(未经微分变换)、一阶微分变换和二阶微分变换; 若α 为小数时, 则为分数阶微分变换。

由于光谱首末段噪声较大, 在预处理时对噪声较大的波段(首末段各50 nm)进行剔除, 剩余450~950 nm波段数据作为大豆冠层反射率光谱数据。依据式(2)在MATLAB 2013b中对提取的大豆冠层光谱数据进行0~2阶微分处理, 阶数间隔为0.1, 得到21种预处理后的冠层光谱数据。

1.2.3 基于分数阶微分算法的植被指数构建

在完成光谱数据预处理后, 依据这些预处理后的光谱数据构建植被指数。植被指数常用来构建作物氮素含量估测模型, 其中两波段组合的归一化差值光谱指数NDSI(normalized difference spectral index)和比值光谱指数RSI(ratio spectral index)能够综合分析光谱数据与氮素含量的相关性, 在作物氮素估测方面取得了较好的效果^{[15, 16]}。本文基于NDSI和RSI的计算方法, 构建了分数阶微分归一化差值光谱指数NDSI_α和分数阶微分比值光谱指数RSI_α, 如式(3)和式(4)所示

$\begin{array}{l} NDS I_{α} (R_{i}, R_{j}) = \frac{R_{α} (i) - R_{α} (j)}{R_{α} (i) - R_{α} (j)} (3) \\ RS I_{α} (R_{i}, R_{j}) = \frac{R_{α} (i)}{R_{α} (j)} (4) \end{array}$

式中, NDSI_α(R_i, R_j)和RSI_α(R_i, R_j)分别代表α 阶下两波段组合构成的归一化光谱植被指数NDSI(R_i, R_j)和比值植被指数RSI(R_i, R_j), R_α(i)和R_α(j)分别代表α 阶预处理后第i和第j个波段对应的光谱反射率。例如, 当α =0时, R₀(i), R₀(j)为原始光谱450~950 nm波段范围内第i和第j个波段对应的光谱反射率; 当α =0.1时, R₀_.₁(i), R₀_.₁(j)为0.1阶微分处理后450~950 nm波段范围内第i和第j个波段对应的光谱反射率。

1.2.4 模型建立与评价

为了验证分数阶微分建立的模型的性能, 分别对各阶微分(整数阶微分和分数阶微分)下的NDSI_α与大豆CNC, RSI_α与大豆CNC进行Pearson相关分析并绘制相关系数等高线图, 得到各阶微分下NDSI_α与大豆CNC, RSI_α与大豆CNC相关系数绝对值的最大值及其对应的波段组合— — 最优波段组合NDSI_α(opt)和RSI_α(opt), 采用线性回归方程, 建立各阶微分下NDSI_α(opt)与CNC, RSI_α(opt)与CNC的预测模型。采用建模集决定系数( $R_{C}^{2}$ )、预测集决定系数( $R_{P}^{2}$ )、建模集均方根误差(RMSEC)、预测集均方根误差(RMSEP)和相对分析误差(RPD)作为模型评价指标, 对各阶微分下建立的模型进行评价。其中 $R_{C}^{2}$ , $R_{P}^{2}$ 越接近1, RMSEC和RMSEP越小, 表明所建模型准确度越好。 RPD代表模型的预测能力, 当RPD小于1.5时, 表明模型预测性能较差, 不能用于预测分析; 当RPD在[1.5, 2.0]之间时, 表明模型效果一般, 可对样品进行粗略估计, 仅能满足一般应用; 当RPD大于2.0时, 表明模型具有较好的预测能力^[17]。

2 结果与讨论

2.1 原始光谱曲线与大豆CNC相关性分析

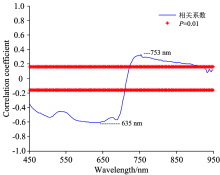
为了验证光谱数据和冠层氮素含量相关数据的有效性, 首先将原始光谱数据与大豆CNC进行相关性分析, 如图2所示。其中, 蓝色曲线是原始光谱与大豆CNC相关性曲线, 红色直线是0.01显著性水平线。由图2可知, 大豆CNC与450~717 nm波段负相关, 而与717~950 nm波段正相关。其中, 光谱反射率与大豆CNC在450~710 nm波段达到极显著负相关(p< 0.01), 在635 nm处相关系数最大为-0.608。在725~925 nm波段, 光谱反射率与大豆CNC极显著正相关(p< 0.01), 在753 nm处相关系数最大值为0.329。可见光波段相关性优于近红外光谱波段。

Figure Option
View Download New Window

图2 冠层光谱反射率与大豆CNC的相关性曲线
注: 粗红线是0.01显著性水平线, 蓝曲线是冠层光谱与大豆CNC相关性曲线Fig.2 Correlation curve between canopy spectra and leaf nitrogen content of soybean plants
Note: The thick red line represents the extreme significant level (P< 0.01). The blue curve is correlation curve between canopy spectra and leaf nitrogen content of soybean plants

2.2 分数阶微分植被指数与大豆CNC相关性分析

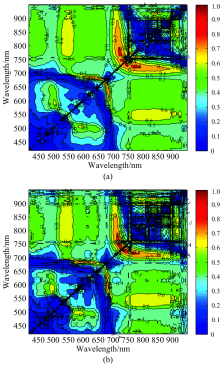
采用Pearson相关性分析法, 对各阶微分下任意两波段组合构成的NDSI_α与大豆CNC, RSI_α与大豆CNC进行相关性分析并绘制相关系数等高线图。例如, 图3是0阶微分下NDSI₀与大豆CNC[图3(a)], RSI₀与大豆CNC[图3(b)]相关系数等势图。由图3(a)可知, 不同波段组合构成的NDSI₀与大豆CNC相关性不同, 可见光波段构成的NDSI₀与CNC相关性较低, 红边平台附近波段构成的NDSI₀与CNC相关性较高。 NDSI₀与CNC相关系数大于0.8的区域是720~730与764~795 nm的波段组合及752~740与740~753 mn的波段组合, 其中NDSI₀(R₅₄₈, R₇₆₇)与CNC相关系数最大, 为0.875 9。由图3(b)可知, RSI₀与CNC相关系数大于0.8的区域包含585~600与684~686 nm的波段组合、 712~722与764~790 nm波段组合、 717~730与732~753 nm波段组合, 其中RSI₀(R₇₂₅, R₇₆₉)与CNC相关系数最大, 为0.828 6。因此将NDSI₀(R₇₂₅, R₇₆₉)和RSI₀(R₇₂₅, R₇₆₉)作为0阶微分下NDSI₀(opt)和RSI₀(opt)的最优波段组合。

Figure Option
View Download New Window

图3 NDSI₀和RSI₀与大豆CNC相关系数等势图
(a): 零阶微分NDSI与大豆的CNC; (b): RSI₀与CNC的相互关系
注: NDSI₀表示基于0阶微分(原始光谱)的归一化差值光谱指数NDSI; RSI₀表示0阶微分(原始光谱)的比值光谱指数RSIFig.3 Contour of correlation coefficient between CNC and NDSI₀, CNC and RSI₀
(a): Correlation between NDSI(0) and CNC; (b): Correlation between RSI(0) and CNC
Note: NDSI₀ represents normalized difference spectral index based on original spectra; RSI₀ represents ratio spectral index based on original spectra

同理, 得到0.1~2阶微分下NDSI_α, RSI_α与CNC相关系数最大值(绝对值)及其对应的NDSI_α(opt)和RSI_α(opt), 如表2所示, 各分数阶微分预处理下得到的NDSI_α(opt)与大豆CNC, RSI_α(opt)与大豆CNC的相关性均达到极显著水平(p< 0.01)。在NDSI_α(opt)与大豆CNC的各阶相关系数中, 0.8阶微分下NDSI_0.8(R₅₄₈, R₇₆₇)与大豆CNC的相关系数最大, 为0.875 9; RSI_α(opt)与大豆CNC的各阶相关系数中, 0.7阶微分下RSI_0.7(R₅₄₈, R₇₆₇)与大豆CNC的相关系数最大, 为0.865 1。

表2 不同分数阶微分下最优植被指数 Table 2 The best vegetation index of different fractional order differentiation

2.3 分数阶微分对相关系数最大值及波段组合的影响

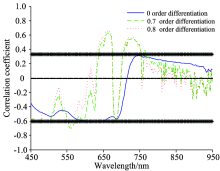
分析各阶微分下NDSI_α(opt)与大豆CNC, RSI_α(opt)与大豆CNC相关系数的变化趋势(图4), 发现随阶数的增加各阶微分下NDSI_α(opt)与大豆CNC, RSI_α(opt)与大豆CNC相关系数均呈先升高后下降趋势, 且NDSI_α(opt)与大豆CNC最大值、 RSI_α(opt)与大豆CNC最大值出现的阶数不同。 NDSI_α(opt)与大豆CNC相关系数最大值在0.8阶出现, RSI_α(opt)与大豆CNC相关系数最大值在0.7阶出现。 0.8阶NDSI_0.8(opt)与0.7阶RSI_0.7(opt)均由R₅₄₈(绿光波段)和R₇₆₇(红边平台波段)两波段光谱反射率组合构成, 而0阶(原始光谱)由R₇₂₅(红边平台波段)和R₇₆₉(红边平台波段)两波段光谱反射率组合构成, 且原始光谱植被指数[NDSI₀(opt), RSI₀(opt)]与大豆CNC的相关系数均小于分数阶微分植被指数[NDSI_0.8(opt), RSI_0.7(opt)]与大豆CNC的相关系数。这是因为虽然红边平台波段与植物叶绿素含量以及氮素营养、生长状态等因素密切相关, 但仅采用红边波段信息对氮素含量进行相关性分析, 不能充分发掘光谱数据中的有效信息, 在氮素含量预测过程中可能存在饱和现象。由图5可见, 分数阶微分预处理能够细化光谱数据的有效信息, 可显著增强红边平台波段与氮素含量的正相关性(635~675 nm, 705~755 nm)及绿波段与氮素含量的负相关性(550~575 nm), 从而提高光谱数据对氮素含量的敏感性。

	Figure Option View Download New Window
	图4 不同阶数下NDSI和RSI与CNC相关系数最大值的的变化趋势Fig.4 Trend of the best correlation coefficient of NDSI and CNC, RSI and CNC under different fractional order differentiation

Figure Option
View Download New Window

图5 0, 0.7, 0.8阶微分下光谱反射率与大豆CNC相关性比较
注: 粗黑线代表原始光谱反射率(0阶微分)与大豆CNC的相关系数的最大值Fig.5 Comparison of correlation between soybean CNC and reflectance spectra under 0, 0.7 and 0.8 order differentiation
Note: The thick black line represent the maximum of correlation coefficient between reflectance spectra (0 order differentiation) and leaf nitrogen content of soybean plants

2.4 分数阶微分对大豆CNC模型的影响

以大豆CNC为因变量, 0~2阶微分预处理后确定的最优NDSI_α(opt)和RSI_α(opt)为自变量, 建立各阶微分下NDSI_α(opt)与CNC, RSI_α(opt)与大豆CNC的线性回归模型(表3, 表4), 分析分数阶微分对大豆CNC建模的影响。在NDSI_α(opt)建立的各阶微分下大豆CNC预测模型中, 基于0.8阶微分NDSI_0.8(R₅₄₈, R₇₆₇)建立的大豆CNC预测模型最优, 其 $R_{C}^{2}$ 为0.767 2, $R_{P}^{2}$ 为0.800 2, RMSEC为4.572 4, RMSEP为3.515 5, RPD为2.250 9。对比0阶、 0.8阶、 1阶、 2阶微分处理后基于NDSI₀(opt), NDSI_0.8(opt), NDSI₁(opt), NDSI₂(opt)建立的大豆CNC预测模型, 发现0.8阶微分建立的模型优于整数阶微分(0阶、 1阶、 2阶), 整数阶微分模型中0阶均优于1阶、 2阶模型, 基于0.8阶微分NDSI_0.8(R₅₄₈, R₇₆₇)建立的模型与0阶微分NDSI₀(R₇₂₅, R₇₆₉)相比 $R_{C}^{2}$ 和 $R_{P}^{2}$ 分别提高了0.062和0.020 3, RMSEC和RMSEP分别降低了0.545 9和0.203 2, RPD提高了0.123。

表3 不同阶微分下NDSI_α(opt)对大豆CNC的建模结果 Table 3 Model results of soybean CNC based on NDSI_α(opt) under different fractional order differentiation

分数阶数	拟合方程	建模集(n=173)		预测集(n=57)
分数阶数	拟合方程	$R_{C}^{2}$	RMSEC/(mg· g^-1)	$R_{P}^{2}$	RMSEP/(mg· g^-1)	RPD
0	Y=353.43X-4.70	0.678 5	5.372 9	0.779 8	3.718 7	2.127 9
0.1	Y=590.46X+5.65	0.702 4	5.169 7	0.753 7	3.908 3	2.024 6
0.2	Y=546.56X+16.36	0.706 8	5.131 4	0.765 9	3.820 8	2.071 0
0.3	Y=451.52X+28.46	0.701 8	5.174 3	0.774 4	3.735 2	2.118 5
0.4	Y=-657.92X+30.96	0.700 4	5.187 2	0.761 3	3.869 7	2.044 9
0.5	Y=494.12X+41.52	0.709 0	5.111 4	0.746 3	4.106 0	1.927 2
0.6	Y=59.17X+38.52	0.712 2	5.083 7	0.688 4	4.499 0	1.758 8
0.7	Y=65.27X+1.63	0.740 5	4.827 0	0.790 4	3.667 2	2.157 7
0.8	Y=47.51X+10.45	0.767 2	4.572 4	0.800 2	3.515 5	2.250 9
0.9	Y=-56.15X+11.74	0.699 7	5.192 5	0.688 6	4.602 9	1.719 1
1	Y=64.42X-2.88	0.701 8	5.174 7	0.730 8	4.093 3	1.933 2
1.1	Y=-43.67X+6.73	0.666 8	5.469 6	0.661 0	4.608 8	1.716 9
1.2	Y=-89.53X+73.52	0.604 5	5.959 2	0.528 8	5.584 9	1.416 8
1.3	Y=-81.97X+67.7	0.582 9	6.119 7	0.501 5	5.746 2	1.377 1
1.4	Y=-72.44X+61.6	0.555 7	6.316 7	0.473 2	5.900 1	1.341 2
1.5	Y=-61.77X+55.47	0.522 8	6.546 3	0.444 4	6.042 5	1.309 5
1.6	Y=-50.61X+49.5	0.484 1	6.806 5	0.415 4	6.172 3	1.282 0
1.7	Y=-39.41X+43.83	0.438 2	7.102 8	0.385 2	6.294 2	1.257 2
1.8	Y=-30.13X+32.95	0.384 1	7.436 8	0.353 0	6.449 1	1.227 0
1.9	Y=-19.97X+30.12	0.321 6	7.804 8	0.313 8	6.591 8	1.200 4
2	Y=291.73X+325.03	0.297 3	7.943 6	0.161 6	7.424 1	1.065 8

注: n表示样本容量

Note: n is the numbers of sample

表3 不同阶微分下NDSI_α(opt)对大豆CNC的建模结果 Table 3 Model results of soybean CNC based on NDSI_α(opt) under different fractional order differentiation

表4 不同阶微分下RSI_α(opt)对大豆CNC的建模结果 Table 4 Model results of soybean CNC based on RSI_α(opt) under different fractional order differentiation

分数阶数	拟合方程		建模集(n=173)				预测集(n=57)
分数阶数	拟合方程		$R_{C}^{2}$		RMSEC/(mg· g^-1)		$R_{P}^{2}$		RMSEP/(mg· g^-1)			RPD
0	Y=-212.46X+204.62		0.686 5		5.305 4		0.783 6		3.692 0			2.143 2
0.1	Y=-319.16X+323.99		0.707 3		5.127 1		0.756 2		3.890 1			2.034 1
0.2	Y=-286.02X+302.21		0.711 9		5.086 7		0.769 5		3.792 3			2.086 5
0.3	Y=-173.19X+201.76		0.708 0		5.120 3		0.733 3		4.134 4			1.913 9
0.4	Y=-169.7X+210.76		0.705 6		5.141 7		0.728 5		4.169 4			1.897 8
0.5	Y=-234.07X+275.37		0.714 1		5.066 6		0.750 1		4.072 4			1.943 0
0.6	Y=-18.38X+55.7		0.723 5		4.982 8		0.725 6		4.138 6			1.912 0
0.7	Y=-63.01X+55.49		0.748 4		4.752 9		0.800 3		3.511 1			2.253 7
0.8	Y=-39.39X+47.28		0.741 8		4.815 5		0.744 1		4.071 3			1.943 6
0.9	Y=20.44X+52.81		0.707 6		5.124 5		0.715 6		4.217 0			1.876 4
1	Y=29.32X+54.09		0.704 9		5.147 6		0.685 9		4.464 1			1.772 6
1.1	Y=38.17X+64.75		0.682 8		5.337 0		0.697 9		4.363 0			1.813 6
1.2		Y=47.74X+63.59		0.648 9		5.614 7		0.673 5		4.583 4	1.726 4
1.3		Y=-10.81X+60.36		0.619 7		5.843 8		0.572 4		5.201 9	1.521 2
1.4		Y=-10.3X+57.41		0.593 8		6.039 8		0.545 9		5.359 1	1.476 5
1.5		Y=-8.13X+53.73		0.561 4		6.275 5		0.520 1		5.499 5	1.438 8
1.6		Y=-8.13X+49.61		0.520 9		6.559 3		0.495 4		5.619 8	1.408 0
1.7		Y=-14.2X+50.76		0.486 0		6.793 5		0.423 9		6.122 0	1.292 5
1.8		Y=-12.62X+46.81		0.458 5		6.973 4		0.403 6		6.228 2	1.270 5
1.9		Y=-11.06X+43.04		0.428 5		7.163 4		0.382 6		6.332 7	1.249 5
2		Y=-9.56X+39.5		0.395 7		7.366 2		0.360 8		6.434 5	1.229 8

注: n表示样本容量

Note: n is the numbers of sample

表4 不同阶微分下RSI_α(opt)对大豆CNC的建模结果 Table 4 Model results of soybean CNC based on RSI_α(opt) under different fractional order differentiation

在RSI_α(opt)建立的各阶微分下大豆CNC预测模型中, 基于0.7阶RSI_0.7(opt)建立的大豆CNC预测最优, 其 $R_{C}^{2}$ 为0.748 4, $R_{P}^{2}$ 为0.800 3, RMSEC为4.752 9, RMSEP为3.511 1, RPD为2.253 7。对比0阶、 0.7阶、 1阶、 2阶微分处理后基于RSI₀(opt), RSI_0.1(opt), RSI₁(opt), RSI₂(opt)建立的大豆CNC预测模型, 发现0.7阶微分建立的模型优于整数阶微分(0阶、 1阶、 2阶), 整数阶微分模型中0阶也均优于1阶、 2阶模型, 0.7阶微分RSI_0.7(R₅₄₈, R₇₆₇)建立的模型与0阶微分RSI₀(R₇₂₅, R₇₆₉)相比 $R_{C}^{2}$ 和 $R_{P}^{2}$ 分别提高了0.061 9和0.016 6, RMSEC和RMSEP降低了0.552 5和0.180 9, RPD提高了0.110 4。

通过对比各阶微分下NDSI_α(opt)与RSI_α(opt)建立的大豆CNC预测模型, 发现基于分数阶微分植被指数(NDSI_0.8(R₅₄₈, R₇₆₇)和RSI_0.7(R₅₄₈, R₇₆₇))建立的大豆CNC模型准确度均高于整数阶微分(0阶、 1阶、 2阶), 其中, NDSI_α(opt)最优预测模型出现在0.8阶, RSI_α(opt)出现在0.7阶, 且均未在整数阶(0阶、 1阶、 2阶)出现。这是因为整数阶微分光谱曲线差异较大, 会忽略光谱渐变信息, 进而影响模型准确度。而分数阶微分能够细化光谱信息, 且充分利用整数阶微分忽略的中间信息, 消除背景噪声对光谱的干扰, 增强光谱对大豆CNC的敏感程度, 提高大豆CNC预测模型的准确度。上述分析表明, 相比整数阶微分, 分数阶微分在大豆CNC定量研究中具有一定的优势。类似的结论也在土壤成分的定量分析中有所体现^{[12, 18]}。

2.5 常用植被指数与分数阶微分植被指数预测大豆CNC效果比较

为进一步综合比较分数阶微分对大豆CNC预测准确度的影响, 本文选择与氮素含量密切相关的5个常用植被指数(VOGII, MTCI, DCNI, NDRE和TCARI)建立大豆CNC预测模型, 并与基于NDSI_0.8(R₇₂₅, R₇₆₉)和RSI_0.7(R₇₂₅, R₇₆₉)建立的模型进行比较, 结果见表5。

表5 常用植被指数与分数阶微分植被指数预测大豆CNC结果比较 Table 5 Comparison of predictive ability of vegetation indices in assessment of soybean nitrogen content

光谱参数	拟合方程	建模集(n=173)		预测集(n=57)			参考文献
光谱参数	拟合方程	$R_{C}^{2}$	RMSEC	$R_{P}^{2}$	RMSEP	RPD	参考文献
VOGII	Y=-752.91X+1.82	0.661 8	5.510 4	0.774 8	3.759 4	2.104 9	[19]
MTCI	Y=36.71X-5.19	0.459 4	6.967 3	0.533 2	5.396 8	1.466 2	[19]
DCNI	Y=6.68X+5.56	0.466 3	6.922 6	0.681 9	4.437 5	1.783 2	[20]
NDRE	Y=253.51X-6.90	0.644 1	5.653 5	0.746 7	3.987 4	1.984 5	[19]
TCARI	Y=-44.91X+55.53	0.539 0	6.434 3	0.656 8	4.692 4	1.686 3	[20]
RSI(0.7)	Y=-63.01X+55.49	0.748 4	4.752 9	0.800 3	3.511 1	2.253 7	本文
NDSI(0.8)	Y=47.51X+10.45	0.767 2	4.572 4	0.800 2	3.515 5	2.250 9	本文

注: n表示样本容量

Note: n is the numbers of sample

表5 常用植被指数与分数阶微分植被指数预测大豆CNC结果比较 Table 5 Comparison of predictive ability of vegetation indices in assessment of soybean nitrogen content

通过表5发现, 除VOG II的RPD值大于2外, 其他四个植被指数RPD值均小于2, 表明VOG II在这五个常用植被指数中具有最优结果。进一步对比基于VOG II, RSI_0.7(R₇₂₅, R₇₆₉)和NDSI_0.8(R₇₂₅, R₇₆₉)建立的大豆CNC预测模型, 发现基于0.7阶RSI_0.7(R₇₂₅, R₇₆₉)和0.8阶NDSI_0.8(R₇₂₅, R₇₆₉)建立的大豆CNC预测模型优于VOG II建立的模型, 其中基于0.7阶微分RSI_0.7(R₅₄₈, R₇₆₇)建立的大豆CNC预测模型与VOG II相比 $R_{C}^{2}$ 和 $R_{P}^{2}$ 分别提高了0.086 6和0.025 5, RMSEC和RMSEP降低了0.757 5和0.248 3, RPD提高了0.146 88, 基于0.8阶微分NDSI_0.8(R₇₂₅, R₇₆₉)建立的大豆CNC预测模型与VOG II相比 $R_{C}^{2}$ 和 $R_{P}^{2}$ 分别提高了0.105 4和0.025 4, RMSEC和RMSEP降低了0.938和0.243 9, RPD提高了0.146, 再次表明分数微分在大豆CNC预测方面具有一定的优势。比较基于RSI_0.7(R₇₂₅, R₇₆₉)和NDSI_0.8(R₇₂₅, R₇₆₉)建立的大豆CNC回归模型, 发现基于RSI_0.7(R₇₂₅, R₇₆₉)建立模型的 $R_{P}^{2}$ , RPD值大于NDSI_0.8(R₇₂₅, R₇₆₉), RMSEP值低于NDSI_0.8(R₇₂₅, R₇₆₉)。因此确定基于RSI_0.7(R₇₂₅, R₇₆₉)建立的模型为本试验中大豆CNC最优模型, 模型预测集实测值与预测值散点图如图6所示, 其R²达到0.800 3。

	Figure Option View Download New Window
	图6 基于RSI_0.7(R₇₂₅, R₇₆₉)的大豆CNC 实测值与预测值的比较Fig.6 Comparison between measured CNC and those estimated using RSI_0.7(R₇₂₅, R₇₆₉)

3 结论

研究探索了不同阶数微分算法下光谱反射率与大豆冠层氮素含量(CNC)的相关性, 评估了不同阶数微分下归一化光谱指数NDSI_α和比值植被指数RSI_α在大豆CNC估算中的预测能力, 得出如下结论:

(1)大豆CNC与冠层光谱反射率在可见光波段负相关, 在近红外波段正相关, 可见光波段其相关性优于近红外光谱波段。

(2)在0~2阶微分范围内, 最优波段组合NDSI_α(opt), RSI_α(opt)与大豆CNC的相关系数随阶数增加均呈现先升高后下降趋势。

(3)与整数阶微分(0阶、 1阶、 2阶)、常用植被指数(VOG II, MTCI, DCNI, NDRE和TCARI)相比, 分数阶微分能够增强红边平台波段与氮素含量的正相关性及绿波段与氮素含量的负相关性, 从而提高大豆CNC预测模型的准确度。

综上所述, 分数阶微分在大豆CNC的定量预测中具有一定的优势, 为作物氮营养检测开拓了新的思路。相信随着研究的不断深入, 分数阶微分在作物营养检测中的应用将更加广泛。

The authors have declared that no competing interests exist.

参考文献

文献列表

[1]	Agaalipour E, Farahvash F, Mirshekari B, et al. Journal of Crop Ecophysiology (Agriculture Science), 2012, 3(23): 235. [本文引用:1]
[2]	Wondimu Bekele, Ketema Belete, Tamado Tana. Forestry and Fisheries, 2016, 5: 1. [本文引用:1]
[3]	ZHAGN Li-ping, WANG Jiu-rong, YUAN Hong-chao, et al(张丽萍, 王久荣, 袁红朝, 等). Hunan Agricultural Sciences(湖南农业科学), 2016, (10): 83. [本文引用:1]
[4]	HE Yong, PENG Ji-yu, LIU Fei, et al(何勇, 彭继宇, 刘飞, 等). Transactions of the Chinese Society of Agricultural Engineering(农业工程学报), 2015, 31(3): 174. [本文引用:1]
[5]	Inoue Y, Sakaiya E, Zhu Y, et al. Remote Sensing of Environment, 2012, 126: 210. [本文引用:1]
[6]	Miphokasap P, Honda K, Vaiphasa C, et al. Remote Sensing, 2012, 4(6): 1651. [本文引用:1]
[7]	LIANG Liang, YANG Min-hua, DENG Kai-dong, et al(梁亮, 杨敏华, 邓凯东, 等). Acta Ecologica Sinica(生态学报), 2011, 31(21): 6594. [本文引用:1]
[8]	XU Ji-gang, FENG Xin-lu, GUAN Liang, et al(徐继刚, 冯新泸, 管亮, 等). Control and Instruments in Chemical Industry(化工自动化及仪表), 2012, 39(3): 347. [本文引用:2]
[9]	Dadras S, Momeni H R. Asian Journal of Control, 2014, 16(2): 489. [本文引用:1]
[10]	Xu M, Yang J, Zhao D, et al. Bio-Medical Materials and Engineering, 2015, 26(s1): 1325. [本文引用:1]
[11]	ZHANG Wen-wen, YANG Ke-ming, XIA Tian, et al(张文文, 杨可明, 夏天, 等). Science Technology and Engineering(科学技术与工程), 2017, 17(25): 33. [本文引用:2]
[12]	WANG Jing-zhe, Tashpolat·Tiyip, DING Jian-li, et al(王敬哲, 塔西甫拉提·特依拜, 丁建丽, 等). Transactions of the Chinese Society of Agricultural Engineering(农业工程学报), 2016, 32(21): 161. [本文引用:3]
[13]	ZHOU Zi-xuan, YU Na, ZOU Hong-tao, et al(周子铉, 虞娜, 邹红涛, 等). Journal of Irrigation and Drainage(灌溉排水学报), 2015, 34(7): 45. [本文引用:1]
[14]	HUANG Guo, XU Li, PU Yi-fei(黄果, 许黎, 蒲亦非). Application Research of Computers(计算机应用研究), 2012, 29(2): 414. [本文引用:1]
[15]	Wang B, Chen Jing, Ju Weimin, et al. Remote Sensing, 2017, 9(3): 291. [本文引用:1]
[16]	QIN Zhan-fei, CHANG Qing-rui, XIE Bao-ni, et al(秦占飞, 常庆瑞, 谢宝妮, 等). Transactions of the Chinese Society of Agricultural Engineering(农业工程学报), 2016, 32(23): 77. [本文引用:1]
[17]	Kamruzzaman M, Elmasry G, Sun D W, et al. Analytica Chimica Acta, 2012, 714(3): 57. [本文引用:1]
[18]	WANG Jing-zhe, Tashpolat·Tiyip, ZHANG Dong(王敬哲, 塔西甫拉提·特依拜, 张东). Transactions of The Chinese Society of Agricultural Machinery(农业机械学报), 2017, 48(5): 152. [本文引用:1]
[19]	Ranjan R, Chopra U K, Singh A K, et al. International Journal of Remote Sensing, 2012, 33(20): 6342. [本文引用:1]
[20]	LI Zhen-hai, XU Xin-gang, JIN Xiu-liang et al(李振海, 徐新刚, 金秀良, 等). Scientia Agricultura Sinica(中国农业科学), 2014, 47(19): 3780. [本文引用:1]

2012

0.0

... 引言氮素与作物的生长发育、产量和品质密切相关, 快速、准确地获取氮素含量是作物长势评价和施肥调控的基础^[1,2] ...

2016

0.0

... 引言氮素与作物的生长发育、产量和品质密切相关, 快速、准确地获取氮素含量是作物长势评价和施肥调控的基础^[1,2] ...

2016

0.0

... 传统的氮素检测方法主要有凯氏定氮法、碱蒸馏法、靛酚蓝比色法、杜马斯燃烧法, 这些检测方法具有检测灵敏度高、结果准确的优点, 但因检测周期长、操作复杂、同时具有破坏性, 导致无法实现作物氮素含量在时间和空间上的连续动态监测^[3] ...

2015

0.0

Yong

, PENG

Ji-yu

, LIU

Fei

, et al(何勇, 彭继宇, 刘飞, 等). Transactions of the Chinese Society of Agricultural Engineering(农业工程学报), 2015, 31(3): 174.

该文阐述了应用光谱和成像技术进行作物养分生理信息快速检测的主要研究进展和发展趋势。介绍了光谱和成像技术的基本原理、常用数据处理方法、建模方法和模型评价指标，重点总结了光谱和成像技术在5种常见农作物（水稻、小麦、油菜、玉米、大豆）的养分生理信息检测中的应用成果和研究进展（主要包括叶绿素类和氮素检测，病虫害、水分、杂草、重金属、农药胁迫诊断及产量预测等方面），分析了光谱和成像技术在作物生长信息检测的发展趋势。结果表明，光谱和成像技术能够快速无损获取作物养分生理信息，并能有效地对作物长势和逆境胁迫响应进行动态监测，对实现农业的精准化、数字化、信息化及智能化管理和作业具有重要意义。

... 作物光谱信息能够反映作物的生化组分、胁迫程度、病害情况等生长信息, 是生物、非生物因子共同作用的体现^[4] ...

2012

0.0

... Inoue等^[5]采用一阶微分比值光谱指数准确地估测了水稻冠层氮素含量 ...

2012

0.0

... Miphokasap等^[6]利用甘蔗冠层一阶微分光谱数据实现了甘蔗冠层氮素含量的估测 ...

2011

0.0

LIANG

Liang

, YANG

Min-hua

, DENG

Kai-dong

, et al(梁亮, 杨敏华, 邓凯东, 等). Acta Ecologica Sinica(生态学报), 2011, 31(21): 6594.

The nitrogen content of canopy leaves of wheat ( Triticum aestivum L.) is one of the most important indices for monitoring wheat growth and yield. The Kjeldahl procedure as the common method for N assays is time-consuming, labor intensive and invasive. As a modern technique, hyperspectral remote sensing is an effective and non-invasive method for rapid estimation of plant nitrogen contents. In this study, a novel hyperspectral index, first derivative normalized difference nitrogen index (FD-NDNI), was developed to estimate the nitrogen content of wheat canopy by hyperspectral remote sensing technology. A total of 190 canopy samples of wheat ranging from jointing to booting stage were scanned by a FieldSpec Pro FR spectrometer, and the spectral data were then assigned randomly to calibration (142 data) and prediction (48 data), respectively. The data were pretreated by wavelet threshold denoising before analysis. Using the fist derivative spectra at 525, 570 and 730 nm and the methods of difference, ratio and normalization, 12 new hyperspectral indices were developed to quantify the nitrogen content of wheat canopy. These indices were then compared with 22 commonly used hyperspectral indices including mNDVI705, mSR and NDVI705. The accuracy of the index FD-NDNI developed was higher than that by the hyperspectral indices commonly used, as indicated by a calibration coefficient of determination ( C-R 2 ) of 0.818 and a predicted coefficient of determination ( P-R 2 ) of 0.811 of the estimation predicted by FD-NDNI. A further analysis showed that the FD-NDNI index described an exponential equation, thererfore the FD-NDNI prediction was concise and unaffected by passivation. The sensitivity analysis of the susceptibility of FD-NDNI to interference of canopy density showed that the R 2 of the correlation between FD-NDNI and the leaf area index (LAI) was 0.536, which was lower than that between the commonly used hyperspectral indices and LAI. FD-NDNI was least sensitive to LAI among the hyperspectral indices and therefore least affected by canopy density when used to estimate the nitrogen content of wheat canopy. FD-NDNI was therefore an ideal spectral index sensitive to prediction, but insensitive to interference. An algorithm of the least squares support vector regression (LS-SVR) was finally used to optimize the FD-NDNI model. A step-search procedure in which a long step size was set first to determine the range of values and then followed by a short step size to determine the specific values, was carried out for rapid optimization of the penalty coefficient C and the RBF kernel function parameter g of LS-SVR models. When the parameters C and g reached the optimal values of 6.4 and 1.6, respectively, the C-R 2 and P-R 2 of the model reached 0.846 and 0.838, respectively, which were higher than those of the exponential model, and indicated that the LS-SVR model was more accurate. The results suggested that FD-NDNI was an optimal hyperspectral index for estimation of the nitrogen content of wheat canopy, and LS-SVR algorithm was a preferred modeling method.

提出了一种估测小麦冠层氮含量的新高光谱指数--微分归一化氮指数(FD-NDNI)。以FieldSpec Pro FR地物光谱仪采集拔节后至孕穗前小麦的冠层光谱190份,随机抽取142份作为训练集,其余48份作为预测集。将光谱以小波阈值去噪法去噪后,利用其525、570 与730 nm处的一阶导数值,采用差值、比值以及归一化的方法构建了12种光谱指数以实现小麦冠层氮含量的估测,并与mNDVI705、mSR以及NDVI705等22种常用指数进行了比较分析。发现指数FD-NDNI对小麦冠层氮含量的估测结果最佳,其估测模型(指数形式)校正集决定系数( C-R 2 )与预测集决定系数( P-R 2 )分别达0.818与0.811,优于mNDVI705等常用指数。进一步分析表明,在各指数中,FD-NDNI对叶面积系数最不敏感,可最有效地避免冠层郁闭度等因素对氮含量估测的影响。为优化结果,采用最小二乘支持向量回归算法(LS-SVR)对模型进行了改进,当模型惩罚系数 C 与RBF核函数参数 g 取得最优解6.4与1.6时,其 C-R 2 与 P-R 2 分别提高至0.846与0.838,具有比指数模型更高的精度。结果表明:FD-NDNI是小麦冠层氮含量估测的优选指数,LS-SVR为建模的优选算法。

... 梁亮等^[7]采用一阶微分归一化氮指数进行小麦冠层氮素含量预测 ...

2012

0.0

... 分数阶微分是整数阶微分的推广, 相比整数阶微分, 在背景噪声去除、有效信息提取等方面更具优势, 已广泛应用于图像识别、信号处理等领域^[8,9,10] ...

... nwald-Letnikov微分定义形式已在光谱数据处理和信息提取方面有广泛应用^{[8, 11,12]}, 本文采用Gr#cod#x000fc ...

2014

0.0

2015

0.0

2017

0.0

... 张文文等^[11]发现分数阶微分预处理能够提高玉米冠层光谱与叶片铜含量的相关性 ...

... nwald-Letnikov微分定义形式已在光谱数据处理和信息提取方面有广泛应用^{[8, 11,12]}, 本文采用Gr#cod#x000fc ...

2016

0.0

... 王敬哲等^[12]应用分数阶微分对荒漠土壤有机碳含量进行估算, 发现分数阶微分比整数阶微分具有更高的预测准确度 ...

... nwald-Letnikov微分定义形式已在光谱数据处理和信息提取方面有广泛应用^{[8, 11,12]}, 本文采用Gr#cod#x000fc ...

... 类似的结论也在土壤成分的定量分析中有所体现^{[12, 18]} ...

2015

0.0

... 为获取有代表性样本数据, 试验依据三因素二次正交回归试验原则^[13], 采用尿素(N)、磷酸二氢钙(P)、硫酸钾(K)进行定量施肥, 每个品种设置15个肥料处理、 1个对照处理(不施肥), 两个品种共计32个处理, 每个处理下设置4次重复, 共种植128盆 ...

2012

0.0

... nwald-Letnikov和Caputo定义^[14] ...

2017

0.0

... 植被指数常用来构建作物氮素含量估测模型, 其中两波段组合的归一化差值光谱指数NDSI(normalized difference spectral index)和比值光谱指数RSI(ratio spectral index)能够综合分析光谱数据与氮素含量的相关性, 在作物氮素估测方面取得了较好的效果^[15,16] ...

2016

0.0

2012

0.0

... 0时, 表明模型具有较好的预测能力^[17] ...

2017

0.0

... 类似的结论也在土壤成分的定量分析中有所体现^{[12, 18]} ...

2012

0.0

2014

0.0

Zhen-hai

, XU

Xin-gang

, JIN

Xiu-liang

et al(李振海, 徐新刚, 金秀良, 等). Scientia Agricultura Sinica(中国农业科学), 2014, 47(19): 3780.

【Objective】Prediction of grain protein content (GPC) can provide effective decision-making supporting information for acquisition and processing of high quality wheat. The objective of the study is to demonstrate the feasibility of remote sensing monitoring of wheat grain protein content based on nitrogen translocation theory, and its expansibility between regional and annual level. 【Method】Field experiments of four winter wheat cultivars by four nitrogen applications in Beijing during 2012-2013 growing seasons were carried out for model building. Firstly, the two main sources of grain nitrogen accumulation and their relationships were analyzed based on nitrogen translocation theory and agronomy parameters modeling. The nitrogen remobilization from vegetative organs to grain was considered as the key point, while the nitrogen uptake from the root absorption during grain filling stage was simply calculated as the nitrogen remobilization from vegetative organs to grain multiplied by a factor. Mechanism of predicting GPC with leaf nitrogen content (LNC) at the flowering stage was clarified through integrating agronomy parameters modeling. Meanwhile, the temperature factor was considered. Secondly, twenty-four vegetative indices were selected according to the good relationship between vegetative indices and leaf nitrogen content, and remote sensing estimating of LNC was established by using grey relational method and partial least squares method (GRA-PLS). Therefore, a prediction model of GPC with remote sensing was established. 【Result】The results showed that the selected five vegetative indices according to grey relational grade were mND705, NDVIcanste, Readone, DCNI and NDCI. For the LNC estimating, the determination coefficient (R2) and corresponding to root mean square error (RMSE) of modeling and validation results were 0.859, 0.257% and 0.726, 0.063%, respectively. Estimation of LNC has good robustness by using GRA-PLS method. The R2 and RMSE of predicted and measured GPC of modeling and validation results were 0.726, 1.30% and 0.609, 1.19%, respectively. The results indicated that it was available to estimate GPC by integration model of nitrogen translocation theory and GRA-PLS method. 【Conclusion】The integration model with explanatory and expansibility could explain the theory of “why the LNC is used to predict GPC”, achieved prediction of grain protein content between regional and annual levels, and had a wide range of potential applications.

1 Beijing Research Center for Information Technology in Agriculture, Beijing 100097 2 National Engineering Research Center for Information Technology in Agriculture, Beijing 100097 3 Institute of Applied Remote Sensing & Information Technology, Zhejiang University, Hangzhou 310029 4 Key Laboratory of Crop Genetics and Physiology of Jiangsu Province, Yangzhou University, Yangzhou 225009, Jiangs

【目的】及时、有效地预测籽粒蛋白质含量，能够为优质小麦品种的收购和加工提供科学合理的决策支持信息。本研究从籽粒蛋白质形成的氮素运转规律出发，研究冬小麦籽粒蛋白质遥感预测的可行性及在区域与年际间的扩展性，为高分辨率遥感卫星进行大面积蛋白质预测提供理论依据。【方法】利用2012—2013年4个冬小麦品种×4个氮肥梯度的试验数据和地面高光谱数据进行建模；基于小麦籽粒蛋白质形成的氮素运转机理，通过分析籽粒氮素累积量的两个主要来源及其之间的比例关系，重点抓住开花前的植株氮素累积量再运转这一主要来源，而灌浆期根际的氮素直接吸收则通过其与前者的比例关系来确定，通过相关农学参数模型的耦合，同时加入温度影响因子对籽粒氮素运转的影响，初步阐明了利用开花期小麦叶片氮含量可以预测籽粒蛋白质含量的应用机理；然后选择与叶片氮含量相关的植被指数，利用灰色关联分析-偏最小二乘算法（GRA-PLS）选择与叶片氮含量关联度较高的植被指数并进行小麦叶片氮含量的估算，通过与氮素运转模型的耦合构建了基于氮素运转原理的籽粒蛋白质含量遥感预测模型；最后利用2009—2010年的品种×播期×肥料试验和2012—2013年的其他品种氮肥处理试验进行验证。【结果】（1）通过GRA方法对叶片氮含量和植被指数间的关联度进行计算，选择关联度较大的前5个植被指数进行叶片氮含量建模，其植被指数分别为mND705、NDVIcanste、Readone、DCNI和NDCI；（2）通过PLS方法构建的叶片氮含量模型，建模结果的预测值与实测值的决定系数（R2）和均方根误差（RMSE）分别为0.859和0.257%，验证结果的R2和RMSE分别为0.726和0.063%，利用GRA-PLS方法估算叶片氮素含量具有较好的稳定性；（3）构建的蛋白质预测模型，建模结果和验证结果的预测值与实测值的R2和RMSE分别为0.713、1.30%和0.609、1.19%，预测模型具有较高的精度与可靠性。【结论】基于氮素运转规律构建的小麦籽粒蛋白质含量遥感预测模型，可以作为应用开花期遥感信息来预测籽粒蛋白质含量的机理性解释，初步实现了本研究区域和年际间的籽粒蛋白质含量预测，具有一定的应用前景。