拉曼光谱分析技术诞生于1928年, 近年来, 随着光电及微电子技术的快速发展, 激光核心设备日趋成熟, 其低成本、 快速、 非接触、 微样本的特点, 使拉曼光谱技术在众多领域得到广泛认可。 在生物体拉曼光谱检测过程中, 为了观察快速变化的动态过程, 如肿瘤细胞的分裂过程, 需要采用较短的积分时间(如0.5 s)以提高光谱测量的时间分辨率^[1]; 或者在农作物病菌识别中, 采用低功率激发光源工作模式(如10 mW, 5 mW)以防止灼烧作物体。 短时积分和低功率光源往往会产生极强的背景噪声, 其强度可能高达被测物质指纹信息的几倍至几十倍。 因此有必要针对生物样本, 研究低信噪比拉曼光谱去噪方法。

拉曼光谱去噪方法有快速傅里叶变换、 小波变换和多项式拟合等, 这些方法在特定情况下均可以有效去除拉曼光谱中噪声。 但是存在滤波参数先验性选取问题, 即不同的截止频率、 滤波窗口长度和基函数、 阈值、 分解层数、 拟合阶数等对去噪效果影响很大^{[2, 3]}。 2009年李卿用经验模态法(empirical mode decomposition, EMD)分解拉曼光谱, 通过低通阈值法实现了拉曼光谱自适应去噪, 但是对于生物体拉曼光谱, EMD法存在模态混叠问题, 低通阈值法无法区分高幅值噪声和高频拉曼信号。 作者在之前研究中应用总体均值经验模分解(ensemble empirical mode decomposition, EEMD)法解决了上述问题, 但是该方法对SNR≤ 10 dB的信号降噪效果不明显。 针对低信噪比生物体拉曼光谱, 本文提出用补充总体均值经验模分解(complementary ensemble empirical mode decomposition, CEEMD)方法处理生物体光谱信号, 既解决了EMD方法中模态混叠问题, 又降低EEMD分解后重构误差, 并应用归一化排列熵(normalization permutation entropy, NPE)定量评估特征模态分量中随机噪声, 从而实现低信噪比拉曼光谱的自适应去噪, 称之为局部补充总体均值经验模分解方法(local complementary ensemble empirical mode decomposition, LCEEMD)。

LCEEMD算法由三部分构成, 首先CEEMD分解拉曼光谱, 该过程具有二进滤波特征^[4], 在依次排列的本征模态分量中, 低阶是高频分量, 通常随机噪声和部分高频拉曼信号会包含其中, 低信噪比光谱去噪的关键是准确识别这两部分信号; 其次, 应用归一化排列熵区分高频非线性序列; 最后应用变阈值过滤随机噪声并重构光谱信号。 具体如下:

(1)正负成对加入高斯白噪声, 对光谱信号r进行j阶EMD分解, 得到本征模态分量c_j, j=1, 2, …, n;

(2)检测c_j是否是无序噪声序列, 如果是, 执行步骤(3); 如果不是, 执行步骤(4)。 检测标准为归一化排列熵值h^s(p), 如果h^s(p)大于阈值θ 则认为该分量为异常信号(间歇或无序噪声等引起模态混叠的高频信号), 若h^s(p)小于阈值θ 则该分量不是异常信号;

(3)噪声分量c_j滤波,

cj(t)=sign[cj(t)][cj(t)-hs(p)σj2lnn]hs(p)≥0.5cj(t)hs(p)< 0.5(1)

其中σ _i为噪声的标准差;

(4)去噪信号重构, r=∑j=1ncj。

其中CEEMD和归一化排列熵原理及详细计算方法参见文献[4, 5, 6]。

通过两个实验, 对比EMD, EEMD和LCEEMD三种方法的滤波效果。

试验一目的: CEEMD既可以解决EMD中模态混叠问题, 又可以提高EEMD重构精度。

EMD方法是Huang提出的一种信号自适应时频分解方法, 该方法多数情况可以将非线性非平稳信号有效分解成其固有频率分量, 例如信号 X1=x1+x2, 其中x1=t2cos(2π×40t), x2=e-t2cos(2π×10t),EMD分解获得两个本征模态分量c₁和c₂, 与组成分量x₁, x₂完全一致; 如果分量之间频率接近, 如 X2=x1+x3, 其中x3=e-t2cos(2π×38t),EMD分解仅得到一个分量即混叠模态X₂。 可见EMD无法筛分相近频率, 而拉曼光谱中噪声和信号均属于高频范畴, 使用EEMD方法可以较好解决模态相似时的混叠问题, 不足之处是信号重构会引入较多白噪声(图1所示), 残留噪声对生物体拉曼弱信号的分析影响较大, 这也是造成低信噪比拉曼信号去噪效果不佳的主要原因。 综上, 应用CEEMD方法分解拉曼光谱, 正负成对加入的白噪声对重构信号影响很小, 图1中蓝色点线和黑色CEEMD重构曲线基本重合, 信号X₂的CEEMD(添加白噪声标准差为0.1, 分解次数100, 最大迭代次数10 000)重构偏差是1.122 6; EEMD(添加白噪声标准差为0.1, 分解次数100)重构偏差为2.361 7× 10¹⁵。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 基于EEMD和CEEMD去噪数据重构信号X2Fig.1 X2 reconstructed by data denoised by EEMD and CEEMD

CEEMD是以EEMD为基础的改进算法, 其克服了EMD中模态混叠, 并有效降低EEMD重构偏差, 所以文中提出基于CEEMD分解拉曼光谱, 以提高信号重构的准确性。

实验二目的: 对于低信噪比仿真信号, LCEEMD去噪效果优于EMD和EEMD。

在信号X₂中添加10 db信噪比白噪声, 得到含噪信号XN₂。 基于EMD, EEMD分别分解XN₂, 对应得到9和10个特征模态分量, 从低阶模态开始逐级对分量进行滤波。 去噪指标采用文献中的信噪比(signal to noise ratio, SNR)、 均方根误差(root mean square error, RMSE)和相关系数(correlation coefficient, r)。 当SNR_i+1> SNR_i, RMSE_i+1< RMSE_i, R_i+1> R_i时, 第i+1次滤波是必要, 并需要进行第i+2次, 否则终止滤波过程。 根据上述终止准则, 分别对EMD和EEMD分解后信号进行2阶和3阶软阈值滤波, 滤波后重构信号如图2(a)所示。 CEEMD中所添加正负白噪声幅值N_std和添加数量没有理论选择规则, 按照经验N_std为原始信号标准差的0.1~0.5倍, 数量在100以内, 对信号分解的影响不大^[5]。 文中添加白噪声Nstd为0.1, 分解次数为100, 最大迭代次数Maxiterate为10 000; 一般白噪声的排列熵为0.9, 间歇性噪声大于0.6^[7], 排列熵值小于0.5的序列内包含噪声可能性微小^[8], 文中噪声排列熵初始阈值为0.5, 步长为0.05, 调整范围0.5≤ θ ₀< 1, 重构信号如图2(b)所示。

观察图2(a)和(b), LCEEMD去噪后数据与原始数据拟合误差小, 好于EMD和EEMD。 进一步通过去噪指标比较上述三种方法的滤波效果, 如表1所示。

图2

Fig.2

	Figure Option ViewDownloadNew Window
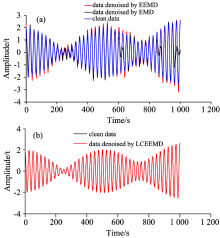	图2 (a)EMD和EEMD去噪数据; (b)LCEEMD去噪数据Fig.2 (a) data donoised by EMD and EEMD; (b) data donoised by LCEEMD

表1

Tabel 1

表1(Tabel 1)

表1 EMD, EEMD和LCEEMD去噪效果比较 Tabel 1 Comparison between data from EMD, EEMD and LCEEMD EMD EEMD LCEEMD SNR 7.970 3 13.413 39.615 0 RMSE 0.448 5 0.239 7 0.001 17 r 0.916 9 0.978 5 0.999 9

表1 EMD, EEMD和LCEEMD去噪效果比较 Tabel 1 Comparison between data from EMD, EEMD and LCEEMD

表1中, EMD去噪处理后数据的信噪比为7.970 3 db, 低于未处理数据信噪比, 说明其低阶模态分量中除了包含噪声, 还混有高频信号, 低阶阈值滤波使其丢失了部分特征信号; 而LCEEMD方法不仅有效解决了模态混叠问题, 还以归一化排列熵为依据判断噪声成分, 避免了EMD方法过度滤波的问题, 获得了近4倍的信噪比。 EEMD去噪后重构信号中有较多噪声残留, 所以其对信噪比提高不多, LCEEMD方法对各模态中噪声按照排列熵不同分别处理, 滤波更加细致, 在三种方法中获得了最低RMSE和最高r。

用加拿大Aura拉曼光谱仪采集人体食指指肚处光谱(激光激发波长为785nm, 曝光时间1 s, 分辨率8 cm^-1), 光谱经过去背景和特征峰增强处理后如图3所示, 可见光谱中残留较强噪声干扰, 对于弱谱峰几乎无法识别, 另外虚假的谱峰高度降低了生物体中微量物质定量分析精度。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 手指拉曼光谱原始数据Fig.3 Raw Raman data of finger

分别用EMD, EEMD和LCEEMD方法对图3拉曼光谱滤波处理, 结果如图4(a), (b), (c)所示。

图4

	Figure Option ViewDownloadNew Window
	图4 (a)EMD去噪拉曼数据; (b)EEMD去噪拉曼数据; (c)LCEEMD去噪拉曼数据

Fig 4 (a) Raman data donoised by EMD; (b) Raman data donoised by EEMD; (c) Raman data donoised by LCEEMD

图4(c)基线平直光滑, 微小特征峰最少, 其是否存在过度去噪以及谱线形变, 下文通过特征谱峰的拉曼归属进行验证。 Caspers研究指出, 1 665 cm^-1特征峰是由螺旋构象的酰胺Ⅰ 带激发散射产生, 1 061, 1 128和1 296 cm^-1均来自脂质的贡献, 其中前两个谱带鉴定为来自角质层的延伸脂质, 所有三个谱带都是神经酰胺的拉曼光谱的强特征, 图4(c)在上述位置准确呈现了4个特征强峰; 另外, LCEEMD处理后的1 080, 1 061和1 128 cm^-1谱峰强度相当, 与文献[9]中测量结果完全一致; 1 747cm^-1处微小峰也没有丢失, 该峰归因于(C=O)酯振动, 其大量存在于甘油三酸酯中^[10]。 表2中详细计算出上述特征峰峰强A、 峰位ν 和峰宽σ 的变化以及特征峰总变化量。

ΔA=16∑iAi-A'i(2)Δν=16∑iνi-ν'i(3)Δσ=16∑iσi-σ'i, i=1, …, 6(4)ΔF=ΔA+Δν+Δσ(5)

其中A', ν '和σ '为降噪后峰强、 峰位和峰宽, Δ F为特征峰变化总量。

表2

Table 2

表2(Table 2)

表2 EMD, EEMD和LCEEMD去噪后特征峰改变情况 Table 2 Changes of characteristic peak denoised by EMD, EEMD and LCEEMD EMD EEMD LCEEMD Δ A 0.262 7 0.306 5 0.007 3 Δ ν 5.333 3 0 0 Δ σ 5.708 8 8.362 4 0.501 3 Δ F 11.304 8 8.668 9 0.508 6

表2 EMD, EEMD和LCEEMD去噪后特征峰改变情况 Table 2 Changes of characteristic peak denoised by EMD, EEMD and LCEEMD

表2中, 大量残留噪声使EEMD处理后光谱谱峰高度和谱峰面积变化均大于EMD方法, 而粗糙的模态分离模式使EMD滤波后谱峰位置发生较大位移, 6个特征峰中有4个发生了一个分辨率的位移, 多次数据试验发现, 这种漂移不具备向左或向右方向上的的一致性。 LCEEMD方法处理后光谱具有最小峰位变化, 其有利于特征峰定位, 避免了重复测量和仪器校准, 以及具有最小峰强和峰面积改变, 其是构成拉曼光谱定量建模和预测精度的重要保障。

接下来以水稻叶片中可溶性糖含量为例, 进一步比较三种方法滤波后数据的定量模型测量精度。

图5是基于美国DeltaNu拉曼光谱仪采集得到水稻叶片拉曼光谱, 为了避免激光灼伤稻苗, 设置激光功率10 mW, 激发波长785 nm, 曝光时间3 s。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 水稻叶片原始拉曼光谱Fig.5 Raw Raman data of rice leaf

共获得上述光谱数据40组, 其来自不同浓度营养液培养的水稻植株。 剔除1组异常数据, 筛分出29组代表性数据构成校正集合, 剩余10组数据用来预测, 可溶性糖含量对照值来自蒽酮法测量。

分别用EMD, EEMD和LCEEMD方法对稻株光谱去噪, 处理后数据用NIRSA(江苏大学与南京林业大学开发化学计量学分析软件)建立神经网络预测模型。 模型输入层节点为6个神经元: 853, 1 125, 1 170, 1 264, 1 340和1 460 cm^{-1 [11]}。 可溶性糖含量为输出节点, 隐含层节点数为10个, 得出3层前馈反向传播神经网络模型。 目标误差为1 mg· kg^-1, 经学习12 503~15 944次后, 系统误差趋于收敛, 得到模型校正相关系数(correlation coefficient, CC)、 预测相关系数(prediction coefficient, PC)、 校正标准误差(standard error of correction, SEC)和预测标准误差(standard error of prediction, SEP), 如表3所示。

表3

Table 3

表3(Table 3)

表3 EMD, EEMD和LCEEMD去噪数据构造模型的参数 Table 3 Model indicators denoised by EMD, EEMD and LCEEMD EMD EEMD LCEEMD CC 0.522 0 0.835 2 0.882 6 PC 0.511 4 0.638 2 0.871 7 SEC 1.002 5 1.009 4 0.983 5 SEP 1.647 8 1.508 8 0.912 0

表3 EMD, EEMD和LCEEMD去噪数据构造模型的参数 Table 3 Model indicators denoised by EMD, EEMD and LCEEMD

表3中可见, EMD滤波数据建立的可溶性糖计算模型, 校正相关系数和预测相关系数较低, 模型无法实际应用; EEMD处理后模型校正集合指标较EMD方法改善, 但是预测相关系数和预测标准误差提高不多; LCEEMD方法取得了稳定的预测集合指标, 其四项指标均优于EMD和EEMD模型。

(1)LCEEMD方法可以自适应处理拉曼光谱中噪声, 与小波、 快速傅里叶等传统方法比较, 无需设置去噪基函数, 分解层数以及阈值等参数;

(2)与其他自适应去噪方法比较, 如EMD, EEMD软阈值法, LCEEMD方法滤波后拉曼光谱获得了最小的峰位、 峰高和峰面积变化, 以及最大预测相关系数和最小预测标准误差。

(3)LCEEMD克服了EMD算法中模态混叠, 降低了EEMD算法中残留噪声, 进一步通过多尺度排列熵计算出分量中噪声成分, 针对低信噪比数据, 获得了优于EMD和EEMD的去噪效果。