基于块稀疏学习的光谱基线校正方法

引用本文

陈苏怡, 李浩然, 戴继生. 基于块稀疏学习的光谱基线校正方法. 光谱学与光谱分析, 2022,42(12): 3730-3735
CHEN Su-yi, LI Hao-ran, DAI Ji-sheng. Baseline Correction Method Based on Block Sparse Signal Recovery. Spectroscopy and Spectral Analysis, 2022,42(12): 3730-3735. 复制到剪切板

Doi: 10.3964/j.issn.1000-0593(2022)12-3730-06
Permissions

《光谱学与光谱分析》期刊社所有

基于块稀疏学习的光谱基线校正方法

陈苏怡, 李浩然, 戴继生^*

江苏大学电气信息工程学院, 江苏镇江 212013

*通讯作者 e-mail: jsdai@ujs.edu.cn

作者简介: 陈苏怡, 1996年生, 江苏大学电气信息工程学院硕士研究生 e-mail: 2221907057@stmail.ujs.edu.cn

收稿日期: 2021-11-16 修回日期: 2022-03-18

基金项目: 国家自然科学基金项目(62071206)资助

摘要

光谱数据在采集过程中易发生基线偏移现象, 导致后续的鉴别和分析结果偏离真实值。因此, 在光谱数据分析前, 需利用基线校正技术获取更为准确的光谱数据。基于稀疏贝叶斯学习(SBL)的基线校正方法无需人工选择参数, 基线校正结果在贝叶斯框架下具有最优性。然而, 现有的稀疏贝叶斯建模较为简单, 无法适用于复杂的稀疏结构。在实际应用中, 当纯谱的某些谱峰较宽时, 对应的稀疏向量将具有一定的块稀疏特性。利用额外的块稀疏结构, 有助于进一步提升SBL方法的性能。为了建模稀疏向量的块稀疏结构特性, 在原有的贝叶斯模型框架中引入模式耦合分层模型。得益于稀疏贝叶斯框架固有的学习能力, 引入的模式耦合分层模型可自适应地学习稀疏向量的块稀疏结构, 从而大幅提升了基于SBL的基线校正方法的性能。为验证本文方法的基线校正性能, 首先利用模拟数据集进行仿真实验, 并将该方法与SSFBCSP方法和SBL-BC方法在不同噪声方差条件下进行对比。仿真实验结果表明, 该方法恢复谱峰较宽纯谱的效果提升明显, 特别是当噪声方差较大时, 其他方法的性能均有不同程度的下降, 但该方法依然具有较好的稳定性。蒙特卡罗仿真实验结果也显示该方法纯谱拟合的标准化均方根误差明显优于其他对比方法。最后, 利用色谱数据集与三种矿物的拉曼光谱数据集进行实测数据的基线校正性能验证, 结果表明该方法能产生比其他方法更为平滑的纯谱拟合结果, 且去噪效果更优。

关键词: 光谱分析; 块稀疏; 稀疏贝叶斯学习; 基线校正

中图分类号:O433.4 文献标识码:A

Baseline Correction Method Based on Block Sparse Signal Recovery

CHEN Su-yi, LI Hao-ran, DAI Ji-sheng^*

School of Electrical and Information Engineering, Jiangsu University, Zhenjiang 212013, China

*Corresponding author

Abstract

Baseline deviation often occurs with the spectrum data acquisition, making the subsequent identification and analysis results deviate from the true values. Therefore, it is necessary to utilize the baseline correction technology to obtain more accurate spectrum data before the spectrum data analysis. The sparse Bayesian learning (SBL)-based baseline correction method can provide the optimal baseline correction results within the Bayesian framework, and it does not need to select parameters manually. However, the SBL framework is too simple to apply to complex sparsity structures. In practical implementations, if the peak of the pure spectrum is wide, the corresponding sparse representation vector would exhibit a block-sparsity property. The performance of the SBL method will be further improved if the additional block-sparse structure can be exploited appropriately. To this end, we introduce a coupling pattern model into the SBL framework to adaptively learn the block-sparse structure. Due to the inherent learning capability of the SBL framework, the proposed method can significantly improve the baseline correction performance. We conducted several simulations to evaluate the performance improvement, where the proposed method is compared to SSFBCSP and SBL-BC with different noise variances. The simulation results verify the superiority of the proposed method for wide peak recovery. Specifically, it has good stability when the noise level is high, but the performance of other methods degrades substantially. Monte Carlo simulation results further demonstrate that our method can significantly improve the pure spectrum fitting’s normalized mean square error (NMSE) performance. Finally, one real chromatogram dataset and three Raman datasets are used to validate the performance of the proposed method. The experimental results indicate that our method can produce smoother pure spectrum fitting and better denoising effects than others.

Key words: Spectral analysis; Block sparse; Sparse Bayesian learning (SBL); Baseline correction

文章图片

引言

光谱分析主要包括红外光谱分析、拉曼光谱分析、原子光谱分析等技术, 它能快速测定样品的化学成分含量, 实现无损伤的定性和定量分析, 因此已被广泛应用于农业、食品、医学及化工等领域^{[1, 2, 3]}。然而光谱数据采集过程易受温度、湿度等环境因素影响, 发生基线偏移现象, 从而对样品定性和定量分析的准确性产生较大影响^[4]。因此, 在光谱数据分析前, 需对光谱数据进行适当的基线校正^[5]。

与纯谱相比, 基线的变化较为缓慢^[6]。利用该特性, 国内外研究人员提出了大量光谱基线校正方法。基于惩罚最小二乘(penalized least squares, PLS)算法, 很多文献陆续报道了扩展PLS方法, 例如非对称加权惩罚最小二乘(asymmetrically reweighted penalized least squares, asPLS)^[7], 双重加权惩罚最小二乘基线校正算法(doubly reweighted penalized least squares, drPLS)^[8]以及改进的非对称最小二乘法(improved asymmetric least squares, IAsLS)^[9]。这些基于PLS的方法能够自动更新不对称权重, 但在低信噪比的情况下无法获得较好的基线校正精度性。近年来, 随着压缩感知理论的快速发展, 基于稀疏表示的信号恢复技术在特征选择^[10]、人脸识别^[11]、信道估计^[12]和光谱信号的基线校正^[13]等方面取得长足发展。 Han等最早提出了一种基于稀疏表示的光谱基线校正方法^[14], 其主要思想是通过引入光谱线型冗余字典将纯谱稀疏表示, 然后利用l₁范数最小准则, 同时实现稀疏信号恢复和基线校正。由于采用了l₁范数近似, 上述方法不可避免地存在性能损失。此外, l₁范数相关的正则项难以选择, 且Voigt-like线型冗余字典不足以提供完备的基来准确地实现稀疏表达。随后, Li等提出了一种基于稀疏贝叶斯学习(sparse Bayesian learning, SBL)的基线校正方法(SBL-BC)^[15], 有效解决了l₁范数近似方法性能下降的问题, 所有参数由最大后验概率确定, 避免人工选择正则项, 并引入网格细化技术解决了字典矩阵的偏离网格间隙问题, 获得了较好的基线校正性能。

然而, 现有的稀疏贝叶斯建模方法只适用于简单的稀疏信号恢复, 当纯谱的某些谱峰较宽时, 需多个相邻的高斯线型拟合该谱峰, 则对应的稀疏向量将具有一定的块稀疏特性。 SBL-BC尚无法适用于这种复杂的块稀疏结构。利用额外的块稀疏结构, 有助于进一步提升SBL方法的性能。为了建模稀疏向量的块稀疏结构特性, 我们在原有的贝叶斯模型框架中引入模式耦合分层模型^[16], 使得稀疏向量中每个元素不仅受其对应的超参数影响, 还受相邻两个元素的超参数影响。借助于稀疏贝叶斯框架具有固有的学习能力, 引入的模式耦合分层模型可自适应地学习稀疏向量的块稀疏结构, 大幅提升基于SBL的基线校正方法的性能。

1 问题描述与稀疏贝叶斯建模

1.1 问题描述

假设采集到的数据维度为N的光谱x∈ R^N由纯谱s∈ R^N、基线b∈ R^N和随机噪声n∈ R^N组成, 即

$x = s + b + n$ (1)

构造一个高斯线型矩阵A∈ R^N^×^N, 其第(i, j)个元素为:

$a_{i, j} = e^{(- \frac{1}{2 σ_{j}^{2}} {(i - j)}^{2})}$ (2)

式(2)中, $σ_{j}^{2}$ 为控制线性宽度的方差。若适当选择 ${σ_{j}^{2}}_{j = 1}^{N}$ , 纯谱s在高斯线性矩阵上可近似稀疏表示为

$s = Aw$ (3)

式(3)中, w∈ R^N表示一个稀疏向量, 其非零元素对应s的谱峰。将式(3)代入式(1), 可得

$x = Aw + b + n$ (4)

1.2 稀疏贝叶斯建模回顾

若假设噪声n服从均值为零, 方差为σ ²的高斯分布, 则有

$p (x | w, b, α) = N (x | Aw + b, α^{- 1} I)$ (5)

式(5)中, α =σ ^-2表示噪声精度。与s相比, b变化非常平缓, 其二阶差分的结果Db大部分趋于零, 其中D∈ R⁽^N^-2)×^N表示二阶差分矩阵^[14]。因此, 我们将Db建模为均值为零, 精度为β 的独立分布高斯过程, 即^[15]

$p (b | β) = N (b | 0, (β D^{T} {D)}^{- 1})$ (6)

由于α 和β 未知, 在传统稀疏贝叶斯框架中, 一般假设它们服从伽马分布^[15]

$p (α) = Γ (α | c, d)$ (7)

$p (β) = Γ (β | c, d)$ (8)

式(7)和式(8)中, c和d分别为一个较小的正实数。为了构建w的稀疏先验特性, 假设w服从一个精度向量为γ = ${γ_{j}}_{j = 1}^{N}$ 的高斯分布^[15]

$p (w | γ) = \overset{N}{\prod_{n = 1}} N (w_{n} | 0, diag {γ_{n}}^{- 1})$ (9)

且γ 服从独立伽马分布

$p (γ) = \overset{N}{\prod_{n = 1}} Γ (γ_{n} | c, d)$ (10)

根据上述稀疏贝叶斯模型, 联合分布p(x, Θ )可分解为

$p (x, Θ) = p (x | w, b, α) p (w | γ) p (b | β) p (γ) p (β) p (α)$ (11)

式(11)中, Θ ={w, α , γ , β , b}表示隐藏变量。

由于无法直接获得后验概率分布p(Θ |x)的闭式解, Li等采用变分贝叶斯推理(VBI)求得p(Θ |x)的最优近似解, 同时引入步进梯度算法迭代更新高斯线型函数方差的网格取值, 解决了离网间隙问题^[15]。 SBL-BC的显著优势在于: (1)所有参数由最大后验概率确定, 无需人工参与; (2)基线校正结果在贝叶斯框架具有最优性, 能显著提升光谱基线校正性能。然而, SBL-BC的贝叶斯建模较为简单, 无法适用于复杂的稀疏结构。若s的某些谱峰较宽, 需多个相邻的高斯线型拟合, 这时w具有一定的块稀疏特性。若能充分利用额外的稀疏结构特性, 将有助于进一步提升基于SBL的基线校正方法性能。

2 基于块稀疏学习的基线校正方法

为了建模w的块稀疏结构特性, 本节我们将在贝叶斯框架下引入模式耦合分层模型^[16], 自适应地学习w的块稀疏结构, 大幅提升基于SBL的基线校正方法的性能。

2.1 模式耦合分层模型

为处理随机块状稀疏信号, 我们拟采用文献[16]中提出了模式耦合模型, 其主要思想是: 假设w的每个元素(例如w_n)不仅受其对应的精度影响(即γ _n), 还受相邻元素的精度(即γ _n_-1和γ _n₊₁)影响。因此, 若定义z_n= ${z_{n, 1}, z_{n, 2}, z_{n, 3}}^{T}$ 为一个选择向量, 其取值仅来自于e₁=[1, 0, 0]^T, e₂=[0, 1, 0]^T和e₃=[0, 0, 1]^T, 则w可建模为

$\begin{array}{l} p (w | Z, γ) = \overset{N}{\prod_{n = 1}} ({N (w_{n} | 0, γ_{n - 1}^{- 1} {)}}^{z_{n, 1}} \cdot \\ {N (w_{n} | 0, γ_{n}^{- 1} {)}}^{z_{n, 2}} {N (w_{n} | 0, γ_{n + 1}^{- 1} {)}}^{z_{n, 3}}) \end{array}$ (12)

而z_n建模为均匀类别分布

$p (z_{n}) = {(\frac{1}{3})}^{z_{n, 1}} {(\frac{1}{3})}^{z_{n, 2}} {(\frac{1}{3})}^{z_{n, 3}}$ (13)

进一步, 将式(9)替换为式(12)和式(13), 则联合分布p(x, Θ )可重写为

$\begin{array}{l} p (x, Θ) = p (x | w, b, α) p (w | Z, γ) \cdot \\ p (b | β) p (γ) p (α) p (β) p (Z) \end{array}$ (14)

其中隐藏变量重写定义为Θ ={w, α , γ , β , b, Z}。由于依然无法获得后验分布p(Θ |x)的闭式解, 我们将采用变分贝叶斯推断寻找一个最优的近似解。

2.2 变分贝叶斯推断

依据文献[17], 我们首先将p(x, Θ )分解为

$p (Θ| x) \approx q (Θ) = q (w) q (α) q (γ) q (β) q (b) q (Z)$ (15)

上述分解形式并不唯一, 最优分解形式应最小化p(Θ |x)和q(Θ )的Kullback-Leibler(KL)离散距, 即

$q^{*} (Θ) = \min_{q (Θ)} D_{KL} (q (Θ) | p (Θ| x))$ (16)

KL离散距小, 其相似程度越高。根据变分贝叶斯推导^[17], 式(16)的解为

$\ln q^{*} (θ_{g}) \propto < \ln p (x, Θ) >_{q_{/ g}^{*}}, g = 1, 2, \dots, 6$ (17)

式(17)中, θ _g表示Θ 第g个元素, $q_{/ g}^{*}$ 表示 $\prod_{i \neq g} q^{*} (θ_{i})$ , $\propto$ 表示相等但相差一个常数。由于 $q^{*} (θ_{g})$ 由 $q^{*} (θ_{i})$ 决定, $< \cdot >_{q}$ 表示关于概率密度函数q的期望。

由于q^*(θ _g)取决于q^*(θ _i), i≠ g, 需通过迭代更新获得稳态解。下面我们将依次讨论如何更新各个q(θ _g)。

在更新q(w)时, 有

$\begin{array}{l} \ln q (w) \propto < \ln p (w | Z, γ) + \ln p (x | w, b, α) >_{q (α) q (γ) q (b) q (Z)} \\ \propto - \frac{1}{2} \hat{α} ‖ x - (Aw + μ_{b}) ‖^{2} - \frac{1}{2} w^{T} (Ψ_{1} Λ_{R} + Ψ_{2} Λ + Ψ_{3} Λ_{L}) w \\ \propto - \frac{1}{2} \hat{α} ((x - μ_{b})^{T} (x - μ_{b}) - (x - μ_{b})^{T} Aw - {(Aw)}^{T} (x - μ_{b})) - \frac{1}{2} w^{T} (\hat{α} A^{T} A + Ψ_{1} Λ_{R} + Ψ_{2} Λ + Ψ_{3} Λ_{L}) w \end{array}$ (18)

式(18)中, Ψ _l=diag{φ _1,_l, …, φ _N_,_l}, φ _n_,_l=q(z_n=e_l), Λ =diag{ ${\hat{γ}}_{1}$ , …, ${\hat{γ}}_{N}$ }, Λ _R=diag{ ${\hat{γ}}_{N}$ , ${\hat{γ}}_{1}$ , …, ${\hat{γ}}_{N - 1}$ }, Λ _L=diag{ ${\hat{γ}}_{2}$ , …, ${\hat{γ}}_{N}$ , ${\hat{γ}}_{1}$ }。由此可知, q(w)服从高斯分布

$q (w) = N (w | μ_{w}, Σ_{w})$ (19)

式(19)中

$Σ_{w} = (\hat{α} A^{T} A + Ψ_{1} Λ_{R} + Ψ_{2} Λ + Ψ_{3} Λ_{L})^{- 1}$ (20)

$μ_{w} = \hat{α} Σ_{w} A^{T} (x - μ_{b})$ (21)

在更新q(α )时, 有

$\begin{array}{l} \ln q (α) \propto < \ln p (x | w, b, α) p (α) >_{q (w) q (b)} \\ \propto \frac{N}{2} \ln α - < \frac{1}{2} α ‖ x - Aw - b ‖^{2} >_{q (w) q (b)} + \\ (c - 1) \ln α - dα \\ = (c + \frac{N}{2} - 1) \ln α - α (d + \frac{1}{2} (‖ x - A μ_{w} - μ_{b} ‖^{2} + tr {A Σ_{w} A^{T} + Σ_{b}})) \end{array}$ (22)

由此可知, q(α )服从伽马分布

$d_{α} = ‖ x - A μ_{w} - μ_{b} ‖^{2} + tr {A Σ_{w} A^{T} + Σ_{b}}$ (23)

$q (α) = Γ (α | c + \frac{N}{2}, \frac{d_{α}}{2} + d)$ (24)

$\hat{α} = < α >_{q (α)} = \frac{2 c + N}{d_{α} + 2 d}$ (25)

在更新q(γ )时, 有

$\begin{array}{l} \ln q (γ) \propto < \ln p (w | Z, γ) + \ln p (γ) >_{q (w) q (z)} \\ \propto \overset{N}{\sum_{n = 1}} (< \frac{1}{2} (z_{n, 1} \ln γ_{n - 1} + z_{n, 2} l n γ_{n} + z_{n, 3} \ln γ_{n + 1}) >_{q (z)} - < \frac{1}{2} {w^{T}}_{n} (φ_{n + 1, 1} γ_{n + 1} + φ_{n, 2} γ_{n} + φ_{n - 1, 3} γ_{n - 1}) w_{n} >_{q (w)}) + \\ \overset{N}{\sum_{n = 1}} ((c - 1) \ln γ_{n} - d γ_{n}) \\ \propto \overset{N}{\sum_{n = 1}} ((\frac{1}{2} (φ_{n + 1, 1} + φ_{n, 2} + φ_{n - 1, 3}) + c - 1) \ln γ_{n} - \\ γ_{n} (d + \frac{1}{2} (φ_{n + 1, 1} {\hat{ω}}_{n + 1} + φ_{n, 2} {\hat{ω}}_{n} + φ_{n - 1, 3} {\hat{ω}}_{n - 1}))) \end{array}$ (26)

式(26)中: ${\hat{ω}}_{n} = | μ_{n} |^{2} + Σ_{n, n}, μ_{n} 和 Σ_{n, n}$ 分别表示μ _w的第n个元素和Σ _w的第n个对角元素。由此可得q(γ )服从伽马分布

$d_{γ_{n}} = \frac{1}{2} (φ_{n + 1, 1} {\hat{ω}}_{n + 1} + φ_{n, 2} {\hat{ω}}_{n} + φ_{n - 1, 3} {\hat{ω}}_{n - 1})$ (27)

$q (γ) = \overset{N}{\prod_{n = 1}} Γ (γ_{n} |c + \frac{φ_{n + 1, 1} + φ_{n, 2} + φ_{n - 1, 3}}{2}, d + d_{γ_{n}})$ (28)

γ _n的期望为

${\hat{γ}}_{n} = < γ_{n} >_{q (γ_{n})} = \frac{2 c + φ_{n + 1, 1} + φ_{n, 2} + φ_{n - 1, 3}}{2 d + d_{γ_{n}}}$ (29)

q(β )与q(b)的更新过程与上面相似, 类比可得

$q (β) = Γ (β |\frac{N}{2} + c, \frac{d_{β}}{2} + d)$ (30)

$q (b) = N (w | μ_{b}, Σ_{b})$ (31)

其中

$d_{β} = ‖ D μ_{b} ‖^{2} + tr {D Σ_{b} D^{T}}$ (32)

$\hat{β} = < β >_{q (β)} = \frac{2 c + N}{d_{β} + 2 d}$ (33)

$Σ_{b} = (\hat{α} I + \hat{β} D^{T} {D)}^{- 1}$ (34)

$μ_{b} = \hat{α} Σ_{b} (x - A μ_{w})$ (35)

q(Z)的更新过程可由文献[16]的推导获得, 但在实际应用中, 为了避免过拟合, 我们可简单地采用均匀分布

$q (z_{n} = e_{i}) = \frac{1}{3}, i = 1, 2, 3$ (36)

此外, 为了快速计算式(34)和式(35), 采用与SBL-BC相似的方法, 设 ${\hat{β}}^{(t + 1)}$ = $ρ {\hat{α}}^{(t + 1)}$ , 获得常数矩阵 ${\hat{α}}^{(t + 1)} Σ_{b}^{(t + 1)}$ =(I+ρ D^TD)^-1, 其中与小、中、大数据集对应的ρ 分别设置为10⁵, 10⁷和10^8[15]。

3 实验仿真

3.1节和3.2节中分别采用模拟数据集和真实数据集评估所提方法的性能。在所有仿真实验中, 本文方法初始化参数设置如下: ${\hat{α}}^{(0)}$ =1, ${\hat{γ}}^{(0)}$ =1· 10⁶, $Σ_{b}^{(0)}$ =(I+10⁵· D^TD)^-1, $μ_{b}^{(0)}$ = $Σ_{b}^{(0)}$ x, v⁽⁰⁾=0.2· 1以及δ =0.02。运行环境为Windows 10操作系统, MATLAB版本为R2019a, CPU为Intel Core i9-9900K, 内存为32 GB。

3.1 仿真数据

在仿真1中, 针对指数基线构造的模拟数据集, 将本文方法与SSFBCSP^[14]和SBL-BC^[15]进行比较。假设模拟数据集中纯谱为

$s_{n} = \overset{8}{\sum_{l = 1}} p_{l} \exp (- \frac{(n - {\overset{̅}{μ}}_{l})^{2}}{2 {\overset{̅}{σ}}_{l}^{2}}), n = 1, 2, \dots, 800$ (37)

式(37)中, 均值$\{\bar{μ}_{l}\}_{l=1}^{8}=\{75, 125, 150, 250, 275, 400, 550, 750\}$, 方差$\{\bar{σ}_{l}\}_{l=1}^{8}=\{50, 30, 80, 60, 50, 100, 80, 30\}$峰值{p_l $}_{l = 1}^{8}$ ={0.8, 0.6, 0.5, 0.7, 0.9, 0.4, 0.5, 0.4}; 基线为

$b_{n} = \frac{1}{5} \exp (- \frac{2 n}{500})$ (38)

式(38)中, b_n表示b的第n个元素。针对该模拟数据集, 将噪声方差分别设为σ ²={10^-4, 10^-2, 10^-1}。图1为不同基线校正方法估计出的纯谱, 红色实线为估计出的纯谱, 黑色虚线为真实光谱。由图可知, 当噪声方差较小(即σ ²=10^-4)时, SSFBCSP方法估计出的纯谱性能较差, SBL-BC和本文方法性能均可获得较好的纯谱拟合性能。当噪声方差增大(例如σ ²=10^-1)时, SSFBCSP方法性能下降明显, SBL-BC方法和本文方法的纯谱拟合性能均略有下降。无论噪声方差如何变化, 本文方法都能表现出最优的估计性能。

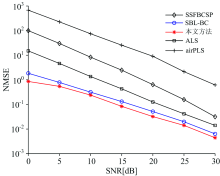
	Figure Option View Download New Window
	图1 模拟指数基线下不同基线校正方法估计的纯谱对比图 (a): 原始光谱; (b): SSFBCSP; (c): SBL-BC; (d): 本文方法Fig.1 Estimated spectrum comparison among different baseline correction strategies for simulated exponential baseline (a): Original spectrum; (b): SSFBCSP; (c): SBL-BC; (d): Our method

在仿真2中, 本文通过蒙特卡罗实验研究了信噪比与纯谱拟合的标准化均方根误差(normalized mean square error, NMSE)的关系, 其中NMSE的定义为

$NMSE = \frac{1}{M} \overset{M}{\sum_{m = 1}} \frac{‖ s_{m}^{e} - s_{m} ‖_{2}^{2}}{‖ s_{m} ‖_{2}^{2}}$ (39)

式(39)中, 蒙特卡罗实验次数M=200, $s_{m}^{e}$ 为第m次实验时对纯谱s_m的估计值。 ALS^[18], airPLS^[8], SSFBCSP^[14]的参数选择与文献[15]一致, 即λ ^ALS=10⁶, p^ALS=0.005, λ ^air=10⁴, λ ₁=10⁵和λ ₂=10^-2。图2为指数基线下纯谱拟合的NMSE与信噪比的关系, 横坐标为信噪比, 纵坐标为NMSE。仿真结果表明, 所有方法的NMSE均随信噪比的增大而减小。无论信噪比如何变化, airPLS的NMSE性能最差, SSFBCSP方法次之, 本文方法与SBL-BC方法均采用了具有更好先验性的稀疏贝叶斯框架, 所以能够表现出较为优异的性能。特别是, 本文方法充分利用纯谱中额外的稀疏结构特性, 自适应的学习稀疏向量的块稀疏结构, 有效地提升了基线校正方法性能。

	Figure Option View Download New Window
	图2 模拟指数基线下随信噪比变化的纯谱拟合NMSE性能对比图Fig.2 NMSE performance comparison of spectrum fitting versus SNR for simulated exponential baseline

3.2 实测数据

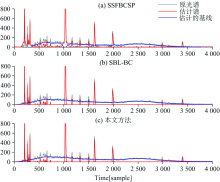
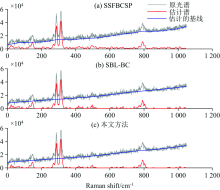
在实测数据实验中, 本文分别使用色谱数据集和三种不同矿物的拉曼光谱数据集(微斜晶石(R040154.3), 准蒙脱石(R050391), 马来石(R040043))进行仿真实验^[15]。将本文方法与SSFBCSP^[14]和SBL-BC^[15]进行比较, 灰色实线为原光谱, 红色实线为估计出的纯谱, 蓝色实线为估计出的基线。

图3为基于色谱数据集估计出的纯谱与基线, 横坐标为时间, 噪声方差设为σ ²=10^-4。图4、图5和图6分别表示基于三种不同矿物的拉曼光谱数据集估计出的纯谱与基线, 横坐标为拉曼位移, 噪声方差均设为σ ²=10^-3。可以看出, 在色谱数据集中, SSFBCSP表现出去噪效果, 但没有对第1 000次样本附近的基线进行校正, SBL-BC方法与本文方法估计出的基线非常相似, 但本文方法获得了更好的光谱信号重构性能, 具有较好的基线校正效果; 微斜晶石数据集中, 本文方法表现出较好的抑制基线偏移的性能; 准蒙脱石和马来石数据集中, 本文方法估计出的纯谱信号更平滑, 可过滤较多的噪声; 对比三种矿物的拉曼光谱数据集, 本文方法表现出了最优的基线校正准确性。

	Figure Option View Download New Window
	图3 色谱数据集的基线校正对比图Fig.3 Comparison of baseline correction for chromatograms dataset

	Figure Option View Download New Window
	图4 微斜晶石数据集的基线校正对比图Fig.4 Comparison of baseline correction for microcline dataset

	Figure Option View Download New Window
	图5 准蒙脱石数据集的基线校正对比图Fig.5 Comparison of baseline correction for paramontroseite dataset

	Figure Option View Download New Window
	图6 马来石数据集的基线校正对比图Fig.6 Comparison of baseline correction for marialite dataset

最后, 表1列出了每个数据集的程序运行时间。可以看出, 对于维度为4 000的数据集, 本文方法的程序运行时间不到5 s, 维度在2 500左右的数据集, 运行时间约为3 s。本文方法执行时间略多于SBL-BC, 但明显少于SSFBCSP, 且本文方法的纯谱拟合与去噪效果明显优于SBL-BC和SSFBCSP方法。

表1 不同基线校正方法的运行时间对比 Table 1 Comparison of the running time of different baseline correction methods

4 结论

在原本的稀疏贝叶斯框架中引入模式耦合模型, 使得稀疏向量中每个元素不仅受其对应的超参数影响, 还受相邻两个元素的超参数影响。为充分利用稀疏向量中的结构特征性, 提出一种基于块稀疏的方法进行基线校正, 解决了稀疏贝叶斯模型由于难以适用于复杂稀疏结构进而导致性能下降的问题。利用指数基线构造的模拟数据集进行实验仿真, 在不同信噪比下将本文方法与SBL-BC等其他方法相对比, 本文方法获得了更精确的纯谱拟合结果。真实数据集的实验对比结果表明, 本文方法较SBL-BC方法获得更精确的光谱信号重构性能, 同时表明了本文方法在实际应用中的普适性。

参考文献

文献选项

[1]	Steffen Cychy, Sebastian Lechler, Zijian Huang, et al. Chinese Journal of Catalysis, 2021, 42(12): 2206. [本文引用:1]
[2]	WANG Qi-ming, TANG Yu-wan, LI Chun-yi, et al(王启明, 唐瑜婉, 李春翼, 等). Food Science(食品科学), 2021, 42(8): 29. [本文引用:1]
[3]	Gamaleev V, Furuta H, Hatta A. IEEE Transactions on Plasma Science, 2019, 47(4): 1841. [本文引用:1]
[4]	WU Jiang-bo, JIA Yun-wei, YAO Cheng-bin, et al(吴江波, 贾云伟, 姚城斌, 等). Spectroscopy and Spectral Analysis(光谱学与光谱分析), 2021, 41(7): 2294. [本文引用:1]
[5]	JIANG Xiao-yu, LI Fu-sheng, WANG Qing-ya, et al(江晓宇, 李福生, 王清亚, 等). Transactions of the Chinese Society for Agricultural Machinery(农业机械学报), 2021, 52(8): 205. [本文引用:1]
[6]	WANG Hai-peng, CHU Xiao-li, CHEN Pu, et al(王海朋, 褚小立, 陈瀑, 等). Chinese Journal of Analytical Chemistry(分析化学), 2021, 49(8): 1270. [本文引用:1]
[7]	Baek S, Park A, Ahn Y, et al. Analyst, 2015, 140: 250. [本文引用:1]
[8]	Xu D, Liu S, Cai Y, et al. Applied Optics, 2019, 58(14): 3913. [本文引用:2]
[9]	He S, Zhang W, Liu L, et al. Analytical Methods, 2014, 6: 4402. [本文引用:1]
[10]	Keinert F, Lazzaro D, et al. IEEE Transactions on Image Processing, 2019, 28(6): 2785. [本文引用:1]
[11]	Wu M, Wang S, Li Z, et al. Applied Intelligence, 2021, 51(11): 8349. [本文引用:1]
[12]	Dai J, Liu A, Lau V K. IEEE Transactions on Signal Processing, 2018, 66(10): 2584. [本文引用:1]
[13]	Dai J, Liu A, So H C. IEEE Transactions on Signal Processing, 2019, 67(4): 1075. [本文引用:1]
[14]	Han Q, Xie Q, Peng S, et al. Analyst, 2017, 142(13): 2460. [本文引用:5]
[15]	Li H, Dai J, Pan T, et al. Chemometrics and Intelligent Laboratory Systems, 2020, 204: 104088. [本文引用:10]
[16]	Lu L, Chen P, Wu L. IEEE Geoscience and Remote Sensing Letters, 2021, 18(4): 672. [本文引用:4]
[17]	Cao Z, Dai J, Xu W, et al. IEEE Signal Processing Letters, 2021, 28: 214. [本文引用:2]
[18]	Vitaly I. Korepanov. Journal of Raman Spectroscopy, 2020, 51(10): 2061. [本文引用:1]

2021

0.0

... 引言光谱分析主要包括红外光谱分析、拉曼光谱分析、原子光谱分析等技术, 它能快速测定样品的化学成分含量, 实现无损伤的定性和定量分析, 因此已被广泛应用于农业、食品、医学及化工等领域^[1,2,3] ...

2021

0.0

2019

0.0

2021

0.0

... 然而光谱数据采集过程易受温度、湿度等环境因素影响, 发生基线偏移现象, 从而对样品定性和定量分析的准确性产生较大影响^[4] ...

2021

0.0

... 因此, 在光谱数据分析前, 需对光谱数据进行适当的基线校正^[5] ...

2021

0.0

... 与纯谱相比, 基线的变化较为缓慢^[6] ...

2015

0.0

... 基于惩罚最小二乘(penalized least squares, PLS)算法, 很多文献陆续报道了扩展PLS方法, 例如非对称加权惩罚最小二乘(asymmetrically reweighted penalized least squares, asPLS)^[7], 双重加权惩罚最小二乘基线校正算法(doubly reweighted penalized least squares, drPLS)^[8]以及改进的非对称最小二乘法(improved asymmetric least squares, IAsLS)^[9] ...

2019

0.0

... ALS^[18], airPLS^[8], SSFBCSP^[14]的参数选择与文献[15]一致, 即#cod#x003bb ...

2014

0.0

2019

0.0

... 近年来, 随着压缩感知理论的快速发展, 基于稀疏表示的信号恢复技术在特征选择^[10]、人脸识别^[11]、信道估计^[12]和光谱信号的基线校正^[13]等方面取得长足发展 ...

2021

0.0

2018

0.0

2019

0.0

2017

0.0

... Han等最早提出了一种基于稀疏表示的光谱基线校正方法^[14], 其主要思想是通过引入光谱线型冗余字典将纯谱稀疏表示, 然后利用l₁范数最小准则, 同时实现稀疏信号恢复和基线校正 ...

... ^N表示二阶差分矩阵^[14] ...

... 1 仿真数据在仿真1中, 针对指数基线构造的模拟数据集, 将本文方法与SSFBCSP^[14]和SBL-BC^[15]进行比较 ...

... ALS^[18], airPLS^[8], SSFBCSP^[14]的参数选择与文献[15]一致, 即#cod#x003bb ...

... 将本文方法与SSFBCSP^[14]和SBL-BC^[15]进行比较, 灰色实线为原光谱, 红色实线为估计出的纯谱, 蓝色实线为估计出的基线 ...

2020

0.0

... 随后, Li等提出了一种基于稀疏贝叶斯学习(sparse Bayesian learning, SBL)的基线校正方法(SBL-BC)^[15], 有效解决了l₁范数近似方法性能下降的问题, 所有参数由最大后验概率确定, 避免人工选择正则项, 并引入网格细化技术解决了字典矩阵的偏离网格间隙问题, 获得了较好的基线校正性能 ...

... 的独立分布高斯过程, 即^[15] ...

... 未知, 在传统稀疏贝叶斯框架中, 一般假设它们服从伽马分布^[15] ...

... = {γj}j=1N的高斯分布^[15] ...

... |x)的最优近似解, 同时引入步进梯度算法迭代更新高斯线型函数方差的网格取值, 解决了离网间隙问题^[15] ...

... 分别设置为10⁵, 10⁷和10^8[15] ...

... 1 仿真数据在仿真1中, 针对指数基线构造的模拟数据集, 将本文方法与SSFBCSP^[14]和SBL-BC^[15]进行比较 ...

... ALS^[18], airPLS^[8], SSFBCSP^[14]的参数选择与文献[15]一致, 即#cod#x003bb ...

... 3), 准蒙脱石(R050391), 马来石(R040043))进行仿真实验^[15] ...

... 将本文方法与SSFBCSP^[14]和SBL-BC^[15]进行比较, 灰色实线为原光谱, 红色实线为估计出的纯谱, 蓝色实线为估计出的基线 ...

2021

0.0

... 为了建模稀疏向量的块稀疏结构特性, 我们在原有的贝叶斯模型框架中引入模式耦合分层模型^[16], 使得稀疏向量中每个元素不仅受其对应的超参数影响, 还受相邻两个元素的超参数影响 ...

... 2 基于块稀疏学习的基线校正方法为了建模w的块稀疏结构特性, 本节我们将在贝叶斯框架下引入模式耦合分层模型^[16], 自适应地学习w的块稀疏结构, 大幅提升基于SBL的基线校正方法的性能 ...

... 1 模式耦合分层模型为处理随机块状稀疏信号, 我们拟采用文献[16]中提出了模式耦合模型, 其主要思想是: 假设w的每个元素(例如w_n)不仅受其对应的精度影响(即#cod#x003b3 ...

... q(Z)的更新过程可由文献[16]的推导获得, 但在实际应用中, 为了避免过拟合, 我们可简单地采用均匀分布 ...

2021

0.0

... 2 变分贝叶斯推断依据文献[17], 我们首先将p(x, #cod#x00398 ...

... 根据变分贝叶斯推导^[17], 式(16)的解为 ...

2020

0.0

... ALS^[18], airPLS^[8], SSFBCSP^[14]的参数选择与文献[15]一致, 即#cod#x003bb ...