引用本文
王青山, 王冬阳, 张雄杰, 汤彬, 吴和喜. 基于高斯锐化法的重叠峰分解方法研究[J]. 光谱学与光谱分析, 2021,41(10): 3245-3250.
WANG Qing-shan, WANG Dong-yang, ZHANG Xiong-jie, TANG Bin, WU He-xi. Research on a Decomposing Method of Energy Spectrum Overlapping Peaks Based on Gaussian Sharpening Method[J]. Spectroscopy and Spectral Analysis, 2021,41(10): 3245-3250.
Doi:10.3964/j.issn.1000-0593(2021)10-3245-06  
Permissions
Copyright©2021, 《光谱学与光谱分析》期刊社
《光谱学与光谱分析》期刊社 所有
基于高斯锐化法的重叠峰分解方法研究
王青山, 王冬阳, 张雄杰*, 汤彬*, 吴和喜
核技术应用教育部工程研究中心(东华理工大学), 江西 南昌 330013
*通讯作者 e-mail: tangbin@ecut.edu.cn; xjzhang@ecut.edu.cn

作者简介: 王青山, 1997年生, 东华理工大学硕士研究生 e-mail: wqs970612@163.com

收稿日期: 2020-08-24 修回日期: 2020-12-30
基金: 国家重大科学研究计划项目(2017YFF0104200), 国家自然科学基金项目(41704171), 国防基础科研项目(JCKY2018401C001), 江西省自然科学基金项目(20192BAB202009), Environmental Radioactivity Research Network Center Project (Ⅰ-2020)资助
摘要

在放射性能谱测量中, 由于探测器分辨率较低、 待测样品中原子能级相近, 往往会出现全能峰的重叠现象, 对放射性核素的定性或定量检测带来较大的困难; 常规的分离算法一般需要复杂的谱变换或大量的标准谱样本, 不适用于现场测量中重叠峰的实时分解。 因此, 提出一种基于高斯锐化法的能谱重叠峰解析方法(GSM), 结合峰锐化法的分辨率增强能力和褶积滑动变换法的平滑特性, 可快速地识别、 定位和解析γ能谱中的重叠峰。 该方法首先对高斯函数进行锐化并做归一化处理, 并以此作为变换算子, 选择合适的高斯参数及窗宽度, 通过对原始γ能谱数据进行褶积滑动变换, 达到滤波和提高重叠峰分离度的目的; 然后求解GSM成形处理后的谱线近似函数作为目标函数, 并选取峰位中心附近若干点作为初始参数, 最后以非线性拟合的方法进行重叠峰特征峰参数的解析。 实验中, 首先验证了该方法变换前后峰位、 峰面积特征值的不变性, 其次分别对重叠峰能谱段以及MCNP模拟的131I,137Cs,214Bi,206Bi和26Al混合放射源γ能谱进行方法验证。 实验结果表明, 该方法对于分离度大于0.375、 信噪比大于40 dB的重叠峰具有较好分解效果, 分解前后的峰位和峰面积的相对误差分别在1%和4.5%以内; 对于γ能谱进行全谱解析后, 重叠峰的峰位分离相对误差在1%以内, 单峰的分离相对误差约为0.1%以内, 且当变换算子的半宽度接近探测器能量分辨率时, 重叠峰的分解结果更准确。 该方法具备较好的噪声抑制性能, 在全谱解析中无需进行能谱光滑及本底扣除等谱线预处理操作, 且计算资源耗费少, 分解精确度较高, 便于能谱测量系统的嵌入式实时解谱应用, 对放射性测量中能谱的现场快速解析具有实用性。

关键词: 重叠峰分解; 峰锐化; 滑动褶积; 非线性拟合
中图分类号:O433.4 文献标志码:A
Research on a Decomposing Method of Energy Spectrum Overlapping Peaks Based on Gaussian Sharpening Method
WANG Qing-shan, WANG Dong-yang, ZHANG Xiong-jie*, TANG Bin*, WU He-xi
Engineering Research Center of Nuclear Technology Application (East China University of Technology), Ministry of Education, Nanchang 330013, China
*Corresponding authors
Abstract

In the measurement of the radioactivity energy spectrum, due to the low resolution of the detector, the similarity of the atomic energy level in the sample to be tested, and the limitation of the instrument stripping technology, the overlapping phenomenon of full energy peak often occurs, which brings great difficulties to the qualitative or quantitative detection of radionuclides. Conventional separation algorithms generally require complex spectrum transformation or a large number of standard spectrum samples and are not suitable for real-time decomposition of overlapping peaks at on-site of measurement. Therefore, a decomposition method of energy spectrum overlapping peaks based on the Gaussian sharpening method (GSM) is proposed, combining the resolution enhancement capability of the peak sharpening method and the smoothing characteristics of the convolution sliding transformation method, which can quickly identify, locate and resolve overlapping peaks in the γ energy spectrum. Firstly, the Gaussian function is sharpened and normalized and selected the appropriate Gaussian parameters and window width, used as a transformation operator to filter and improve the separation of overlapping peaks through convolution and sliding transformation of the original γ energy spectrum data. Then, the approximate function of the energy spectrum after GSM shaping is solved as the objective function, and several points near the center of the peak position are selected as initial parameters. Finally, the analysis of the characteristic peak parameters of the overlapping peaks is carried out by the method of nonlinear fitting. In the experiment, we first verified the invariance of the peak position and peak area eigenvalues before and after GSM shaping, and then the GSM was verified in the overlapping peak energy spectrum and the MCNP simulated131I,137Cs,214Bi,206Bi and26Al mixed radioactive source γ energy spectrum. The experimental results show that GSM has great decomposition ability for the overlapping peak with the resolution better than 0.375 and the SNR better than 40 dB, the relative errors of the peak position and peak area before and after decomposition are within 1% and 4.5%, respectively; For the GSM-processed energy spectrum of γ-ray, the relative error of the position of the overlapping peak is within 1% and that of the single peak is within 0.1%, furthermore, the decomposition result will be more accurate if the half-width in the transformation operator is set close to the energy resolution of the detector. GSM is noise-immune and does not require pre-processing operations such as spectrum smoothing and background subtraction in full-spectrum analysis. Besides, it consumes less computing resources and has high-resolution accuracy, which is convenient for embedded real-time spectrum analysis of energy spectrum measurement system and has practicability for quick on-site analysis of energy spectrum in radioactive measurement.

Keyword: Peak sharpening; Sliding convolution; Nonlinear fitting; Overlapping peak decomposition
引言

γ 能谱测量与分析是放射性信息获取的重要方式, 在辐射监测、 放射医疗、 岩性分析等领域[1]都有广泛的应用。 实际测量中γ 能谱通常会受到环境本底与测量干扰等不可抗力因素的影响, 通常为多种能量和强度不同的γ 射线单能谱的叠加, 特别是能量相近的γ 射线, 往往以重叠峰的形式出现, 且强度弱的γ 谱线又容易被强峰或本底所掩盖, 容易对放射性核素种类的判断及含量的计算造成不利影响。

重叠峰的数值解析技术至关重要, 近年来, 国内外在重叠峰的分解方面进行了较为深入的研究, 如导数法[2]、 正交投影法[3]、 小波分析法[4]、 遗传算法[5, 6]、 人工神经网络模型[6]、 纯元素谱剥离[7]、 粒子群算法[8]等方法。 都月[9]等改进了纵向和平分迭代法, 提出优化迭代重叠峰分解方法, 较传统迭代方法其效率提高了66.7%; 黄洪全等[10]利用高斯混合模型结合期望最大化迭代算法进行γ 谱重叠峰分解; 周世融等[11]提出了峰锐化法结合双树复小波变换的低分离度重叠峰解析方法, 并实现了分离度为0.34的X荧光光谱重叠峰分解。

目前, 重叠峰的分解方法众多且较为成熟, 但是普遍存在卷积过程复杂、 计算资源消耗大、 结果受算法参数影响较大的弊端, 不适用于测量现场能谱快速解析的实际应用。 本文提出一种快速、 低耗的分解重叠峰的新方法, 为放射性能谱测量中重叠峰的现场分解提供支持。

1 高斯锐化方法(GSM)
1.1 峰锐化方法

锐化算法常被应用于图像处理领域中以提高图像的对比度或清晰度, 也可在信号处理领域中用以人为地提高峰的可视分辨率。 在能谱分析中, 对重叠峰进行锐化处理可人为地增大其分离度, 达到分离重叠峰的目的, 通常采用二阶导数或四阶导数来确定峰位置[12], 其算法可表示如式(1)

R(x)=s(x)-ks(2)(x)(1)

式(1)中, R(x)为锐化后的信号, s(x)为原始信号, s(2)(x)为其二阶导数, k为锐化因子, 可平衡信号信噪比和基线平坦度从而调整其大小达到最佳锐化效果。

1.2 褶积滑动变换方法

由于核衰变及测量的统计性, 能谱数据普遍受到统计涨落的影响, 一般通过谱光滑处理以增加定性及定量分析的准确性。 与傅里叶变换法的“ 频域滤波” 不同, 褶积滑动变换法为“ 时域滤波” , 即为变换函数与实验谱线进行卷积变换[13]

F(x)=f(x)* g(x)=∫-mmf(x)·g(x-τ)(2)

式(2)中, F(x)为平滑后的谱线, f(x)为原始谱线, g(x)为变换函数, m为滑动变换的半窗宽。 随着x的增加, g(x)将逐道向前滑动, f(x)经过宽度为2m+1的变换从而转换为新谱线F(x), 当变换函数与峰形状函数相同且半宽度一致时, 光滑效果最优。

1.3 高斯锐化方法

锐化的本质为对信号的微分处理, 当一个噪声信号经过微分后, 信号的噪声同样经过了微分。 因此, 不可利用传统的锐化方法直接对含噪的信号进行运算。 若对谱线平滑进行处理可以提供更高的分辨率, 根据卷积的性质对式(2)变形, 信号F(x)的n阶导数可表示为

F(n)(x)=f(n)(x)* g(x)=f(x)* g(n)(x)(3)

由式(3)可以看出: 对原信号而言, 平滑与微分操作二者的先后顺序并不影响其计算结果。 为了取得平滑后信号的微分, 我们可先对变换函数进行微分得到其平滑算子, 然后利用该平滑算子作为滤波器对原信号进行卷积。 若g(n)(x)选择高斯导数小波, 则信号F(x)的n阶导数便可通过小波变换实现, 高斯小波变换的本质和信号f(x)经过g(x)平滑的n阶导数运算类似。

将锐化后的高斯函数作为高斯锐化算子g(x)可得

g(x)=Gauss(x)-kGauss(2)(x)Gauss(x)=Ae-(x-μ)22σ2(4)

其中, A为高斯锐化算子的峰值, μ为高斯锐化算子的峰位, σ为高斯锐化算子的标准差, k为高斯锐化因子。 为使信号卷积变换前后峰面积保持不变, 高斯锐化算子g(x)作为平滑窗函数还需满足如式(5)关系

∫-mmg(x)=1(5)

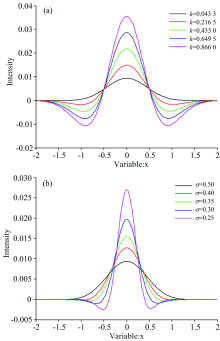
式(5)中, m为半窗宽。 对高斯锐化算子按式(5)进行归一化处理后, 分别取不同的k和σ值, 以探究算子参数对高斯锐化成形效果的影响, 其结果如图1所示。 k值越大, 其峰值越大, 峰宽基本保持不变, 且始终过定点(μ± σ, Ae-1/2), 峰两侧旁瓣的凹陷也越低, 且当k< H2/32时[14](H为算子的半宽度), 将不会出现凹陷; σ值越小, 其峰值越大, 峰两侧旁瓣的凹陷越低, 峰宽越窄。 实际应用中可通过调节k值以优化谱峰的高度, 调节σ值以优化谱峰的分离度, 根据分析需求设定合适的参数。

图1 高斯锐化算子(A=1, μ=0, m=200)
(a): 不同锐化因子k的高斯锐化算子(σ=0.5); (b): 不同标准差σ的高斯锐化算子(k=0.043 3)Fig.1 Gauss sharpening operator (A=1, μ=0, m=200)
(a): Gaussian sharpening operator with different sharpening factor k (σ=0.5); (b): Gaussian sharpening operator with different standard deviation σ (k=0.043 3)

结合式(2)与式(4)可得高斯锐化法(Gauss sharpening method, GSM)递推公式为

F(x)=∑τ=-mmf(x)[Gauss(x-τ)-kGauss(2)(x-τ)](6)

本方法处理噪声信号具有一定的优越性, 既能过滤锐化所引入的噪声又能分辨峰位置、 突出峰形, 实际应用中可根据实际情况选择进行一次或多次高斯锐化成形。

2 仿真实验
2.1 重叠峰模型构建及锐化效果验证

由于核辐射测量数据服从高斯分布, 采用多个高斯函数的叠加以仿真能谱重叠峰

f(x)=∑i=1nAie-(x-μi)22σi2+noise(7)

式(7)中, n为重叠的高斯峰个数, Ai为高斯峰的高度, μi为高斯峰的峰位, σi为高斯峰的标准差, noise为叠加的噪声信号, 以仿真谱线中的统计涨落影响。

重叠峰中不同组分的峰高、 峰宽和峰位置参数将影响峰的重叠程度, 通常采用分离度[11]来判断相邻两峰的分离程度

Rs=|μ1-μ2|2(σ1+σ2)(8)

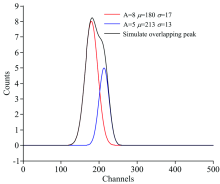
式(8)中, μ1和μ2分别为两峰的峰位置, σ1和σ2分别为两峰的峰宽。 即使没有噪声的信号, 当分离度过小时, 重叠的两个峰也很难分辨, 本文实验所用分离度均取0.3以上, 并模拟一组重叠峰(如图2所示)

y=8e-(x-180)22×172+5e-(x-213)22×132+noise(9)

其分离度为0.55, 并利用MATLAB中“ awgn” 函数添加60 dB高斯白噪声。 由于采用的信号是已知特征参数的峰信号, 因此可通过比较处理结果与原特征参数来衡量峰分辨效果。

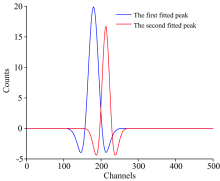
图2 重叠峰示意图(SNR=60 dB)Fig.2 Overlapping peak model (SNR=60 dB)

根据传统锐化成形式(1)和高斯锐化成形式(6), 分别对式(9)所示的重叠峰进行处理, 其结果如图3所示。 可明显看出经过锐化的信号其峰宽变窄、 峰幅值变大、 分离度变大、 峰形状更加明显且独立。 传统锐化成形后的信号分辨率明显下降, 其信噪比仅为19.5 dB, 而高斯锐化法成形结果的分辨率有了明显的提高, 其信噪比约为52 dB。

图3 重叠峰两种锐化结果对比
(a): 传统锐化成形结果(k=46); (b): 高斯锐化成形结果(A=1.12, k=5, m=5, μ=0, σ=0.5)Fig.3 Comparison of two sharpening results of overlapping peaks
(a): Traditional sharpening results (k=46); (b): Gaussian sharpening result (A=1.12, k=5, m=5, μ=0, σ=0.5)

高斯锐化法具有较好的噪声抑制性能, 重叠峰分离效果显著, 且成形前后峰面积的标准差约为0.008 4, 可认为其成形前后峰面积保持不变, 为能谱的定量分析提供实验结果支撑。

2.2 基于非线性曲线拟合的重叠峰参数提取

对给定数据, 使得拟合函数与其误差平方和最小化原则, 寻求与给定点的距离平方和最小的曲线h(x), 经过GSM成形的信号服从式(7)分布, 经过化简变形可得

h(x)=AFe-(x-μF)22σF2{σF4+kF[σF2-(x-μF)2]}σF4(10)

式(10)中, AF, μF, kF和σF均为拟合参数, 本文使用MATLAB中lsqcurvefit工具, 以式(10)作为期望函数进行非线性拟合, 并对其进行峰位、 峰面积计算, 以验证高斯锐化算法的有效及准确性。

在非线性拟合中初始值的选择非常重要, 若选择不当, 则计算结果不一定收敛。 为了避免了曲线拟合的不唯一性, 提高曲线拟合结果可信度。 本文以各个子峰峰位为中心, 取7个点或9个点进行拟合, 得到各个子峰的初始参数, 再将其作为曲线拟合的初始值, 拟合结果如图4所示。 模拟的标准高斯重叠峰均实现完全分解, 且峰位和峰面积的相对误差分别在0.006%和0.03%以内。 结果表明, 峰锐化法结合褶积滑动变换可快速且较准确地分解标准高斯重叠峰。

图4 重叠峰GSM非线性拟合结果Fig.4 Nonlinear fitting results of overlapping peak by GSM

为探究GSM对重叠峰参数提取准确性, 本文分别选取分离度为0.55, 0.45和0.375的重叠峰, 并逐次降低重叠峰分辨率, 依次进行高斯锐化处理并提取重叠峰参数。 其中高斯锐化算子参数选取A=1/ 2/π4, μ=0, σ=0.5, k=5, m=49, 将实验结果与标准谱峰信息对比分析, 结果如表1和表2所示。

表1 标准高斯重叠峰模型的GSM峰位分解结果/% Table 1 Peak position decomposition result of GSM for standard Gaussian overlapping peak model/%
表2 标准高斯重叠峰模型的GSM峰面积分解结果/% Table 2 Peak area decomposition result of GSM for standard Gaussian overlapping peak model/%

利用高斯锐化法可对能谱段进行重叠峰分解并提取相关参数。 对于高分辨率(SNR≥ 50 dB)谱线, 即使分离度为0.375时也可以达到优良的分解效果, 误差可控制在1%以内; 对于低分辨率谱线(SNR≤ 30 dB), 其误差均高于5%, 且在分离度为0.375时已经完全失真。 结合上述分析, 利用该方法可对SNR≥ 40dB, RS≥ 0.375的谱线实现较好的分离效果。

3 基于蒙特卡洛方法的模拟能谱解析

根据国际原子能机构(IAEA)提供的核数据资料, 214Bi核素的γ 衰变能量为609.32 keV, 137Cs核素的γ 衰变能量为661.675 keV, 二者相差52.355 keV; 206Bi核素的γ 衰变能量为1 718.7 keV, 26Al核素的γ 衰变能量为1 808.65 keV, 二者相差89.95 keV。 当混合放射源中包含上述核素时, 特别是在使用NaI(Tl)闪烁探测器等低分辨率的探测器时, 能谱谱峰将严重重叠。

为较好地仿真实验条件, 利用MCNP对131I, 137Cs, 214Bi, 206Bi和26Al组合放射源进行模拟, 根据实验时所用仪器的探头, 模型中采用ϕ 30 mm× 50 mm的圆柱型NaI(Tl)晶体作为探头材料, 密度为3.67 g· cm-3。 晶体外侧包裹一层0.05 cm厚的MgO反射层, 底部的SiO2光学玻璃厚度为0.2 cm, 侧面和前面用0.2 cm的Al壳包裹, 探头外围空间用空气填满, 其结构如图5所示。

图5 探测器模型
1: NaI; 2: Air; 3: MgO; 4: Al; 5: SiO2Fig.5 Detector model
1: NaI; 2: Air; 3: MgO; 4: Al; 5: SiO2

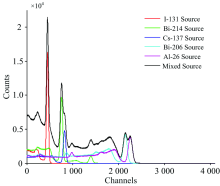
利用F8计数卡计算放射源的γ 射线在NaI(Tl )晶体中的脉冲高度能谱分布, 所测5种放射源的γ 能谱如图6所示, 求得131I谱峰(364.489 keV)、 137Cs谱峰(661.675 keV)、 214Bi谱峰(609.32和1 120.294 keV)、 206Bi谱峰(1 718.7 keV)和26Al谱峰(1 808.65 keV)峰位分为451, 757, 823, 2 145和2 258道。

图6 基于MCNP的混合源模拟γ 能谱Fig.6 Mixed source simulated γ energy spectrum based on MCNP

该混合源γ 能谱图存在两组重叠峰, 且完全无法识别出137Cs核素全能峰的位置。 对原始谱线直接进行GSM处理可快速进行全谱分析并对其中重叠峰进行分解, 无需进行能谱平滑以及扣除本底操作。 GSM全谱分解的结果如图7所示, 分解误差如表3所示。

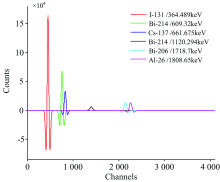图7 混合源模拟γ 能谱的GSM分解结果Fig.7 Decomposition result of simulating γ energy spectrum of mixed source by GSM

表3 模拟γ 能谱的GSM数值解析结果 Table 3 Numerical analysis results of simulated γ energy spectrum by GSM

对于单峰而言, 处理前后峰位近似不变; 对于重叠峰而言, 分解前后误差在1~3道之内, 二者相对误差均在1%以内。 实验结果证明, 利用高斯锐化法能够快速、 高效地对γ 能谱进行全谱解析且重叠峰分解结果较为精确。

4 结论

提出一种高斯锐化法快速全谱分析并分解重叠峰的新方法。 仿真实验结果表明, 该方法具备较好的噪声抑制性能, 且能对SNR≥ 40 dB, RS≥ 0.375的重叠峰有较好的分解效果。 同时, 利用该方法对MCNP模拟的混合源γ 能谱进行全谱解析, 实现了放射性核素全能峰的有效分解。

该方法的特点和优势为: (1)无需进行能谱平滑及扣除本底操作, 即使在康普顿坪的影响下也可得到较准确的结果; (2)计算资源消耗低, 能谱变换仅需一次滑动卷积便可完成, 便于集成化能谱测量系统中机器语言的实现, 在工业应用中具有实用性; (3)受统计涨落的影响较小且分解结果较为精确。

参考文献
[1] TANG Wei, ZENG Guo-qiang, GAO Yan, et al(唐伟, 曾国强, 高妍, 等). Nuclear Techniques(核技术), 2019, 42(1): 010402. [本文引用:1]
[2] Wahab M F, O’Haver T C, Gritti F. et al. Talanta, 2019, 192: 492. [本文引用:1]
[3] CHEN Di-zhao, CUI Hui(陈迪钊, 崔卉). Chinese Journal of Chromatography(色谱), 2000, 18(2): 100. [本文引用:1]
[4] Muhammad Farooq Wahab, Thomas C O’Haver. Journal of Separation Science, 2020, 43(9-10): 1998. [本文引用:1]
[5] HUANG Fan, ZHANG Xu-kun, SUN Lu, et al(黄凡, 张旭坤, 孙陆, 等). Laser & Optoelectronics Progress(激光与光电子学进展), 2020, 57(9): 093001. [本文引用:1]
[6] Xiong Jingyi, Liang Wei, Liang Xiaobin, et al. Process Safety Progress, 2020, 39: e12129. [本文引用:2]
[7] LIU Ming-bo, LIAO Xue-liang, HU Xue-qiang, et al(刘明博, 廖学亮, 胡学强, 等). Metallurgical Analysis(冶金分析), 2019, 39(8): 19. [本文引用:1]
[8] LIU Hong-li, HUANG Hong-quan, YANG Xi, et al(刘红莉, 黄洪全, 杨熙, 等). Nuclear Electronics & Detection Technology(核电子学与探测技术), 2019, 39(1): 83. [本文引用:1]
[9] DU Yue, MENG Xiao-chen, ZHU Lian-qing(都月, 孟晓辰, 祝连庆). Journal of Applied Optics(应用光学), 2019, 40(3): 461. [本文引用:1]
[10] HUANG Hong-quan, HE Zi-shu, FANG Fang, et al(黄洪全, 何子述, 方方, 等). Atomic Energy Science and Technology(原子能科学技术), 2010, 44(9): 1114. [本文引用:1]
[11] ZHOU Shi-rong, HE Jian-feng, REN Yin-quan, et al(周世融, 何剑锋, 任印权, 等). Spectroscopy and Spectral Analysis(光谱学与光谱分析), 2020, 40(4): 1221. [本文引用:2]
[12] Li Yuan-lu, Wang Qi, Sun Ning, et al. Spectroscopy Letters, 2013, 46(7): 507. [本文引用:1]
[13] Alaeddine H H, Bazzi O, Alaeddine A H, et al. IEICE Transactions on Fundamentals of Electronics, Communications and Computer Sciences, 2012, E95. A(6): 1007. [本文引用:1]
[14] Tom O’Haver. Pragmatic Introduction to Signal Processing, 2020: 71. [本文引用:1]