作者简介: 徐志钮, 1979年生, 华北电力大学电气与电子工程学院副教授 e-mail: wzcnjxx@sohu.com
为了在保证测量准确性的基础上提高基于布里渊散射的光纤分布式传感的实时性, 对布里渊频移的快速、 高精度提高算法进行了研究。 实现了基于二次多项式拟合的布里渊频移提取算法和典型的基于洛伦兹、 高斯、 伪Voigt和Voigt模型的算法, 采用光时域反射计(BOTDR)实测了一段长光纤上的布里渊谱, 采用以上算法提取了对应的布里渊频移。 计算结果表明, 二次多项式拟合算法的计算速度明显快于以上经典算法, 其计算耗时仅分别为以上经典算法的1.15%, 1.80%, 1.51%和0.51%, 但计算误差明显大于经典算法, 影响了其实际应用。 以上结果与对应数值产生布里渊谱的计算结果吻合。 为了提高该算法的计算准确性, 系统研究了扫频范围、 扫频点数、 信噪比、 线宽和扫频范围偏差对基于二次多项式的布里渊频移提取准确性的影响。 结果表明: 当扫频点数固定时随扫频范围增加布里渊频移误差先减少到最小值后逐渐增加, 扫频点数固定时最佳扫频范围为1个线宽; 扫频范围不变时随扫频点数和信噪比的增加布里渊频移误差分别成幂和指数规律减少; 扫频范围与线宽比值不变及扫频点数不变时随线宽增加布里渊频移误差线性增大; 随扫频范围偏差增加误差逐渐增大, 实际用于拟合的谱信号尽量围绕布里渊频移左右对称。 根据以上研究结果提出了一种用于布里渊频移快速提取的改进二次多项式拟合算法, 该算法从测量得到布里渊谱中截取1倍线宽且关于最大增益对称的谱信号用于后续拟合, 较之经典的谱拟合算法, 改进算法不仅能大幅提高计算速度且计算准确性与经典算法相似。 采用数值产生及实测布里渊谱的计算结果验证了所提出算法的有效性。 提出的算法不仅能有效提高基于布里渊散射的光纤分布式传感的实时性。
To improve real-time performance of fiber distributed sensing based on Brillouin scattering, and at the same time, ensure high measurement accuracy, the topic about Brillouin frequency shift extraction with high accuracy and less computational burden is investigated. The computer programs about Brillouin frequency shift extraction algorithms are based on quadratic polynomial fit and typical Lorentz, Gaussian, pseudo-Voigt and Voigt models are written. Brillouin spectra in a single-mode fiber are measured by the BOTDR (Brillouin Optical Time Domain Reflectometry). The Brillouin frequency shift about these spectra is extracted by the above algorithms. The results reveal that the computational burden of the algorithm based on quadratic polynomial fit is much less than those of the typical algorithms. Its computation time is only 1.15%, 1.80%, 1.51% and 0.51% of those of the typical algorithms. However, its error is much larger than that of the typical algorithms which will obstruct its application. The above results are consistent with the results of the corresponding numerically generated Brillouin spectra. To improve the accuracy in the quadratic polynomial fit algorithm, the influences of frequency sweep span, number of frequency sweep, signal to noise ratio (SNR), linewidth and deviation of frequency sweep span on the error in the extracted Brillouin frequency shift. The results reveal that if the number of frequency sweep is fixed, the error initially decreases with increasing frequency scanning range. Once the minimum error is reached, it may do the very opposite. The optimal frequency scanning scope equals to linewidth. The error varies as a power of the number of frequency sweep. The error also reduces exponentially with SNR (dB). The error is proportional to linewidth. The error increases with increasing deviation of frequency sweep span. Therefore, the spectra used for Brillouin frequency shift extraction should be symmetric about Brillouin frequency shift. According to the above results, a modified Brillouin frequency shift extraction algorithms based on quadratic polynomial fit is proposed. The algorithm selects Brillouin spectra with one linewidth and symmetric about maximum Brillouin gain and used to extract Brillouin frequency shift. The proposed algorithm can considerably decrease computation time relative to the typical algorithm, and at the same time, the accuracy is similar to that of the typical algorithms. The proposed algorithm is validated by the measured spectra and numerically generated spectra. The proposed algorithm not only can significantly improve real-time performance of fiber distributed sensing based on Brillouin scattering.
分布式光纤传感器除具有一般光纤传感器抗电磁干扰、 耐腐蚀以及电绝缘性好等优点外, 还具有只需一次测量即可获取沿整个光纤被测场分布信息等独特优点, 另外其测量精度高、 定位准确、 传感距离可达上百公里。 因此, 应用领域非常广泛。 其中, 基于光纤布里渊散射的分布式传感技术在温度和应变测量上所达到的测量精度、 测量范围以及空间分辨率高于其他类型的分布式光纤传感技术, 因此引起了国内外的广泛关注和研究[1, 2]。 利用该技术对油气管道、 大型水利水电工程结构和电力线缆等的温度和应变进行在线监测, 可实现故障隐患及故障点的快速、 准确定位。
在与温度和应变有关的谱特征量中, 布里渊频移与温度和应变呈线性关系[1]且最为稳定, 目前基于布里渊散射的光纤分布式传感测量时绝大多数需要提取布里渊频移信息。 布里渊频移的准确、 快速测量对基于布里渊散射的光纤分布式传感系统非常关键[3]。 整体上看布里渊频移的提取方法以拟合基于的方法为主, 可以分为模型基于的算法[4, 5, 6, 7, 8]和非模型基于的算法[9]。 由于能充分利用布里渊谱的波形数据来提取布里渊频移, 整体上看模型基于的算法具有更高的准确性。 当入射矩形脉冲宽度明显大于10 ns(大于50 ns)时光纤中实测布里渊谱近似满足洛伦兹函数, 目前洛伦兹模型基于的拟合算法应用最为广泛。 当然, 随着脉冲宽度的增加空间分辨率减少, 为了提高空间分辨率常使用较小的脉冲宽度, 当其值小于10 ns时布里渊谱近似满足高斯分布, 此时更应该采用高斯模型基于的算法。 显然, 这样根据脉冲宽度来选择算法的方式给布里渊频移的提取增加了一个干扰因素, 迫切需要一个通用模型基于的算法。 可以认为在矩形脉冲的整个脉宽范围内布里渊谱更满足Voigt函数[4], 因此Voigt模型基于的算法具有更高的准确性。 但Voigt函数并非代数表达式, 只有数值解[10], 虽然基于它的算法准确性最高但计算速度过慢, 不是特别适合于长传感范围、 高空间分辨率的场合。 为了提高计算速度, 采用洛伦兹和高斯模型线性组合的伪Voigt模型[5, 6]来近似布里渊谱, 具有很好的表征效果。 为了进一步提高计算速度和收敛能力, 人们开展了大量工作。 为了提高布里渊频移提取的准确性, 文献[5, 6]采用有限元分析来改进Newton算法和Levenberg-Marquardt算法, 然后采用不同信噪比和线宽的布里渊谱的计算结果验证了改进算法在精度提高方面的有效性。 针对变量初值选择比较困难可能导致算法发散的问题, 有研究分别采用了布谷鸟牛顿搜索和粒子群优化来获得更加靠近最优解的初值, 然后采用Levenberg-Marquardt算法来优化变量, 能确保收敛。 虽然以上算法提高了准确性、 降低算法发散的概率, 但是该模型所对应的是非线性目标函数, 需要采用迭代优化算法才能得到最优解, 通常情况下计算速度仍然偏慢。 这在传感距离较长、 空间分辨率较高时比较突出。 该问题仍有待于进一步研究。
为了解决这个问题, 本文采用二次多项式逼近布里渊谱从而提取布里渊频移。 实现了本算法和典型的基于洛伦兹、 高斯、 伪Voigt和Voigt模型的算法, 针对实测和仿真布里渊谱的计算发现, 二次多项式拟合算法的计算速度较现有经典模型基于算法有显著提高, 但误差偏大。 此后系统研究了扫频范围、 扫频点数、 信噪比、 线宽和扫频范围偏差对基于二次多项式的布里渊频移提取准确性的影响。 根据研究结果提出了改进的二次多项式拟合算法, 改进的算法不仅能大幅提高计算速度且计算准确性与经典算法相当。 采用数值产生及实测布里渊谱验证了提出算法的有效性。
入射脉冲光为矩形波时会发生布里渊散射, 布里渊谱近似满足如下的Voigt模型, 它是洛伦兹函数与高斯函数的卷积[14]形式
式(1)中, ν 为频率值(GHz); ν B是布里渊频移(GHz); Δ ν BL和Δ ν BG分别为Lorentzian型和Gaussian型布里渊谱的线宽(GHz)。 可以采用计算更为快速的伪Voigt模型来表征布里渊谱, 设布里渊增益谱的线宽为Δ ν B; g01和g02分别为布里渊散射谱的Lorentzian和Gaussian峰值增益, 布里渊谱表示如式(2)
也可以采用二次多项式来逼近布里渊谱, 即
采用二次多项式拟合后布里渊频移计算公式如式(4)
如果计算所得布里渊频移超出了谱的扫频范围, 此时布里渊频移误差可能会超乎正常的大。 故算法实现时选择扫频范围内满足均匀分布的随机值作为计算所得的布里渊频移, 可以减少测量误差且使测量结果显得更正常。
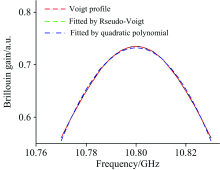
由图1可知, 伪Voigt函数几乎逼近Voigt函数, 而二次多项式虽然与真实的Voigt函数从表达式上看差别不小, 但也有希望逼近对应的谱线。
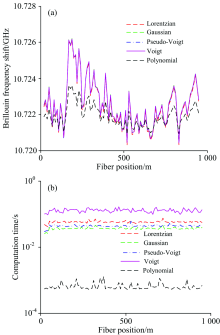
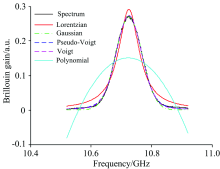
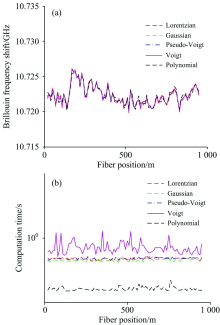
采用中电科仪器仪表有限公司生产的AV6419型光时域反射计(Brillouin optical time domain reflectometry, BOTDR)搭建了光纤布里渊谱测量系统, 选择了约1 km SM 9/125 μ m光纤。 扫频范围为10.52~10.92 GHz, 扫频间隔为1 MHz, 入射脉冲光波长为1 550 nm, 脉冲宽度为10 ns, 采样分辨率为10 m, 叠加平均次数为218。 实验在室温下进行, 但由于绕制光纤承受了应变, 因此沿线布里渊频移并非恒定值。 采用基于洛伦兹、 高斯、 伪Voigt和Voigt模型算法以及二次多项式拟合算法计算, 布里渊频移的提取结果和计算时间如图2所示。 选择一个典型谱5种算法的拟合结果如图3所示。
由图2(a)可知, 基于洛伦兹、 高斯、 伪Voigt和Voigt模型算法的布里渊频移提取结果几乎一致, 这与图3中基于高斯、 伪Voigt和Voigt模型算法的拟合结果能较好逼近实测谱这一结果吻合, 这些结果也基本验证了基于谱模型的布里渊频移提取的可靠性。 然而, 在大部分区域基于二次多项式算法的布里渊提取结果小于其他算法的计算结果, 它与以上4种算法差距的均值分别为0.70, 0.74, 0.73和0.73 MHz, 差距的最大值分别为2.47, 2.60, 2.57和2.60 MHz。 分析认为基于谱模型算法的计算结果比较可靠, 故二次多项式拟合算法存在明显误差, 这与二次多项式拟合结果与实测谱差距较大比较吻合(图3)。 这一结论会在后续分析中得到进一步验证。 由图2(b)可知, 基于Voigt模型算法计算速度最慢, 然后依次是基于洛伦兹、 伪Voigt、 高斯模型的算法, 最快的是二次多项式拟合算法, 图2(b)中5种算法对应的平均计算时间分别为58.97, 37.69, 44.72, 131.48和6.76 ms, 即二次多项式拟合算法的计算时间仅为前4种算法的1.15%, 1.80%, 1.51%和0.51%。 二次多项式拟合算法具有非常快的计算速度, 但计算误差可能偏大, 因此需要改正该算法, 这就是本研究的重点。
本研究不是根据一定温度和应变下光纤布里渊谱数据来分析算法准确性。 因为这种方式通常默认算法计算结果为准确值, 而目前, 二次多项式拟合算法的准确性本身就需要核对, 故不宜采用该方式。 研究中选择信噪比较高信号的原因是过大的噪声可能会掩盖布里渊频移随光纤位置的变化规律。
采用数值产生谱进一步计算的原因是: (1)实测谱虽然可靠但布里渊频移不能足够准确获得; (2)后续涉及大量数值产生谱的分析, 需要验证数值产生谱分析结果的可靠性。 布里渊谱根据式(1)产生, 其中的A, ν B, Δ ν BL和Δ ν BG由Voigt模型算法针对2.1节实测谱计算获得。 信噪比与实测谱一致, 约为33 dB。 布里渊频移的提取结果如图4所示。 5种算法针对一个与图3实测谱对应典型谱的拟合结果如图5所示。
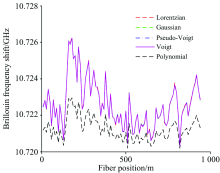 | 图4 不同算法布里渊频移的提取结果, 仿真谱Fig.4 The extracted Brillouin frequency shift of various algorithms, numerically generated spectra |
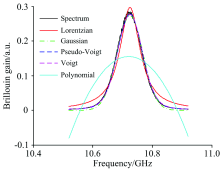 | 图5 不同算法布里渊谱的拟合结果, 仿真谱Fig.5 The fitted Brillouin spectra of various algorithms, numerically generated spectra |
由图4可知, 5种算法算得布里渊频移及随光纤位置的变化规律与实测谱非常接近。 仍然是基于洛伦兹、 高斯、 伪Voigt和Voigt模型算法的布里渊频移提取结果几乎一致, 二次多项式拟合算法计算结果明显小于前者, 这与图2非常吻合。 比较图3和5可知, 实测谱和仿真谱的拟合结果非常吻合。 这验证了数值产生谱信号能较好模拟实测谱。 由于数值产生信号的布里渊频移已知, 据此可知5种算法对应误差幅值的均值分别为0.06, 0.05, 0.05, 0.05和1.35 MHz。 与基于实测谱分析结果基本吻合, 即基于洛伦兹、 高斯、 伪Voigt和Voigt模型算法的准确性足够高, 但二次多项式拟合算法存在显著误差。 基本上验证了本研究中的数值产生谱的可靠性。
若减少二次多项式拟合算法的误差, 需要研究各种因素对该算法准确性的影响规律。 根据系统研究发现数值产生信号时谱模型选择对布里渊频移提取结果影响不大, 同时为了适当加快计算速度, 后续分析采用洛伦兹模型产生谱。 考虑到实际情况多变, 分析时较之实际情况适当扩展了参数的取值范围, 不会减少研究结果的可信度。
g0, ν B和Δ ν B分别取0.9, 10.7, 0.03 GHz; 信噪比设置为10, 20和30 dB; 扫频点数为61; 扫频在0.2Δ ν B~10Δ ν B范围内变化。 针对每种参数组合, 产生10 000个谱信号, 计算后得布里渊频移误差幅值的均值。 二次多项式拟合算法算得的布里渊频移误差如图6所示。
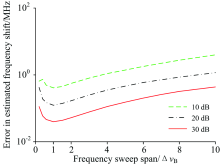 | 图6 布里渊频移误差与扫频范围的关系Fig.6 Change of error in the extracted Brillouin frequency shift with frequency sweep span |
由图6可知, 扫频点数固定时当扫频范围较小时布里渊频移的计算误差较大。 随着扫频范围的增加误差逐渐减小, 当扫频范围为一个线宽时误差达到最小值。 然后, 随着扫频范围的增加误差又逐渐增大。 这是因为扫频范围过小时对应的信号中没有包含足够多的谱特征, 当扫频范围过大时在谱特征提取有效范围内的点数太少。 因此两种情况下的误差均较大。
扫频范围为Δ ν B; 扫频点数N在3~501范围内变化。 其他参数与3.1节一致, 二次多项式拟合算法算得的布里渊频移误差如图7所示。
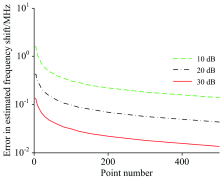 | 图7 布里渊频移误差与扫频点数的关系Fig. 7 Change of error in the extracted Brillouin frequency shift with number of frequency sweep |
由图7可知, 扫频范围不变时随着扫频点数的增加布里渊频移误差逐渐减小。 拟合发现布里渊频移误差幅值的均值Eν B满足: Eν B=aNb, 以上3种情况下a的值分别为3.281 2, 0.858 0和0.267 7, 对应b的值分别为-0.509 5, -0.472 2和-0.471 0, 拟合相对误差分别为3.11%, 4.13%和4.12%。
扫频范围为Δ ν B; 信噪比(signal to noise ratio, SNR)在0~40 dB范围内变化。 其他参数与3.1节一致, 二次多项式拟合算法计算的布里渊频移误差如图8所示。
 | 图8 布里渊频移误差与信噪比的关系Fig.8 Change of error in the extracted Brillouin frequency shift with signal to noise ratio |
由图8可知, 随着信噪比的增加布里渊频移误差逐渐减少。 当信噪比大于10 dB时布里渊频移误差与信噪比近似满足指数规律变化。 当信噪比小于10 dB时误差的变化规律与大于10 dB时不同, 这是因为信噪比较低时直接采用二次多项式拟合算法得到的布里渊频移超出了扫频范围, 算法实现时采用扫频范围内的随机值来作为算得的布里渊频移, 这样可以减少测量误差且使测量结果显得更正常。
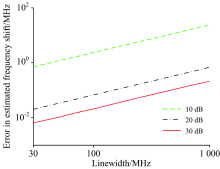
扫频范围为Δ ν B; Δ ν B在0.03~1 GHz范围内变化。 其他参数与3.1节一致, 二次多项式拟合算法算得的布里渊频移误差如图9所示。
由图9可知, 随着线宽的增加布里渊频移误差线性增强。 实际上该规律在扫频范围/线宽不变且扫频点数不变时成立。 因此, 通过选择较窄的入射脉冲光来提高空间分辨率的同时会增加布里渊频移误差。 为了提高布里渊频移的准确性, 应该选择适当配置使布里渊谱线宽减小。
由于待测光纤布里渊频移未能完全准确获得, 扫频范围的中点与布里渊频移未必重合, 二者的差距在本文中称为扫频范围偏差。 扫频范围偏差在0~0.3Δ ν B范围内变化; 扫频范围为Δ ν B。 其他参数与3.1节一致, 二次多项式拟合算法得到布里渊频移误差如图10所示。
 | 图10 布里渊频移误差与扫频范围偏差的关系Fig.10 Change of error in the extracted Brillouin frequency shift with deviation of frequency sweep span |
由图10可知, 随着扫频范围中点逐渐偏离布里渊频移, 布里渊频移误差有增加的趋势。 因此, 应该围绕布里渊频移为中心选择谱信号用于布里渊频移提取。
由上述分析可知, 二次多项式拟合算法对准确性影响较大的因素分别是扫频范围、 扫频点数、 信噪比、 线宽和扫频范围偏差。 虽然扫频点数、 信噪比和线宽对二次多项式拟合算法的准确性影响较大, 但这3个因素主要由实际测量状况决定。 而用于拟合谱的扫频范围和扫频范围偏差可以调整接近最优值以减少算法的误差。 即不再是所有测量信号而是以布里渊频移为中心截取1个Δ ν B的谱信号用于二次多项式算法的拟合。 这样改进的二次多项式拟合算法的准确性能提高, 而且由于待拟合点数的减少二次多项式拟合算法的计算速度会进一步加快。
由于布里渊频移为待测量, 在算法执行前未知, 故实际算法执行时以布里渊谱峰值对应频率为中心截取1个Δ ν B的谱信号用于二次多项式算法的拟合。 线宽虽然与多个因素, 包括光纤密度、 折射率、 石英光纤材料的粘滞系数、 激光器输出中心波长和入射脉冲光宽度等有关, 通常实验布置时除了入射脉冲光宽度其他参数基本固定。 因此, 线宽的估算比较容易。
采用2.1节的实测谱进行分析, 区别在于本节仅仅以增益峰值为中心截取了1个Δ ν B的谱信号。 Δ ν B取实测结果的近似值, 即0.1 GHz。 5种算法的计算结果和计算时间如图11所示。
由图11(a)可知, 基于洛伦兹、 高斯、 伪Voigt和Voigt模型算法的布里渊频移提取结果几乎一致, 与图2(a)吻合。 比较图2(a)与图11(a)可知, 所提出的改进二次多项式拟合算法的计算结果与经典谱模型算法的计算结果非常接近, 与以上4种算法差距的均值分别仅为0.39, 0.24, 0.23和0.26 MHz。 另外, 4种经典算法的布里渊频移提取结果在待拟合谱范围调整前后差别很小, 也进一步验证了以上4种算法的准确性。 图11(b)与图2(b)非常相似, 也是二次多项式拟合算法的计算量远小于其他算法。 以上结果说明了改进二次多项式拟合算法计算量远小于其他经典算法, 但准确性与其他算法接近。
谱参数及谱产生方法与2.2节一致, 但本节以增益峰值为中心截取了0.1 GHz的谱信号用于布里渊频移提取。 5种算法的计算结果如图12所示。
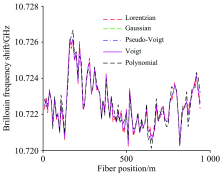 | 图12 本算法与经典算法的布里渊 频移提取结果, 仿真谱Fig.12 The extracted Brillouin frequency shift of the proposed algorithm and the typical algorithms, numerically generated spectra |
比较图11(a)与图12可知, 针对5种算法实测谱和仿真谱的计算结果非常相似, 它与以上4种算法差距的均值分别仅为0.34, 0.21, 0.23和0.24 MHz。 以上4种经典算法及本研究提出的改进算法误差幅值的均值分别仅为0.13, 0.06, 0.06, 0.06和0.24 MHz, 按照典型的温度敏感系数1.2 MHz· ℃-1来估算, 温度单一因素测量时以上5种算法的误差分别为0.11, 0.05, 0.05, 0.05和0.20 ℃。 以上结果进一步验证了改进二次多项式拟合算法的有效性。
采用实测和数值产生的布里渊谱, 对基于二次多项式拟合算法的布里渊频移提取问题进行了系统研究, 在保证实时性的基础上显著提高了计算准确性, 结论如下:
(1)当扫频点数固定时随扫频范围增加布里渊频移误差先减少到最小值后逐渐增加, 最佳扫频范围为1个线宽; 扫频范围不变时随扫频点数和信噪比增加布里渊频移误差分别呈幂和指数规律减少; 扫频范围与线宽比值不变及扫频点数不变时随线宽增加误差线性增大; 扫频范围不变时随扫频范围偏差增加误差逐渐增大, 用于特征提取的谱信号尽量选择围绕布里渊频移左右对称。
(2)二次多项式拟合算法的计算速度远快于基于洛伦兹、 高斯、 伪Voigt和Voigt模型的算法, 但原始二次多项式拟合算法可能存在显著误差。 通过选择合适扫频范围的改进二次多项式拟合算法(以布里渊谱峰值对应频率为中心截取1个Δ ν B的谱信号用于二次多项式算法的拟合)可以在保持快速计算的基础上使准确性与基于洛伦兹、 高斯、 伪Voigt和Voigt模型的算法相似。
本文研究结果为实现光纤分布式传感的快速测量提供了很好的支持。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|