Several parameters are known to affect the quality and the precision of portable XRF (PXRF) analyses, including: sample matrix^{[20, 21]}, interfering elements, sample homogeneity, particle size^{[7, 22]}and soil moisture^{[23, 24, 25]}. In this paper, a total of 52 soil reference materials, purchased from National Research Center for Certified Reference Materials, the People’ s Republic of China, were employed as analysis samples. The soil samples came from Xinjiang, Neimenggu, Sichuan provinces in China, and so on.The contents of heavy metals in these reference materials have been previously detected by chemical analyses (atomic absorption spectrometry, atomic fluorescence spectrometry and X-ray fluorescence spectrometry, et al)and are available online at http://www.bzwz.com/.The XRF measurements of soil reference materials were conducted under room temperature condition (25± 1)℃ with 60% relative humidity to provide standardized measurement conditions.

The equipment used in this study was a field PXRF analyzer NITON XL3t 600 (Thermo Fisher Scientific Corporation, USA), a 40 keV X-ray tube with Ag anode target excitation source, and a Si-PIN-diode with a Peltier cooled detector. The download and export of data from the instrument were facilitated by NITON data transfer software.

EDXRF spectrometry was used to analyze the detection of soil heavy metals. The energy spectra (0~40 keV) were selected to analyze the detection of soil heavy metals.The filter of this instrument has main, high and low filter plates. The test time for each filter plate is set to 30 s. The testing range of heavy metals in each filter plate is different. The four kinds of heavy metals in this study were determined by using the main filter plate and the low filter plate. The heavy metals tested by using the main filter plate were Pb, As and Zn, whereas Cr was tested by usingthe low filter plate.

The steps for detection of heavy metals content in soil by XRF spectrometry were as follows:

Step 1. Soil standard samples were filled into a polyethylene sample cup (diameter 31 mm and height 40 mm) with a collar of fixed Mylar film (thickness 6 μ m). The polyethylene sample cup bottom was sealed by using Mylar film to ensure that there was no sample leakage. Then 2.0 g soil sample was loaded into the sample cup and compressed to provide a smooth sample surface.

Step 2. The sample cup was placed in the testing stand and the side of the cup covered with Mylar film was aimed at the instrument probe window. Sample testing was repeated 5 times. Acquisition time was 90 s.

Statistical analyses were performed by using EXCEL2010, MATLAB R2015a, 2Dshige software and Unscrambler 9.7. Linear regression was performed in EXCEL2010. 2D synchronization correlation spectroscopy was performed in 2Dshige version 1.3 software (2Dshige (c) Shigeaki Morita, Kwansei-Gakuin University, 2004— 2005). A statistical procedure of the data set directly measured from the PXRF instrument was followed using Unscrambler 9.7 (CAMO Software, AS). The PLSR quantitative models were established in MATLAB R2015a (The MathWorks, Inc., Natick, MA, USA). Simple linear regression and 2D synchronization correlation spectroscopy were introduced in some detail below.

1.3.1 Simple linear regression

For each element, a simple linear regression model was used to investigate the relationship between the real concentrations and those measured by PXRF. The relationship produced a linear model

y=ax+b+ε

where y is the PXRF concentration, x is the real concentration, b is the intercept of the regression line, a is the slope, and ε is the residual in the regression equation. The correlation coefficient and standard error were employed to determine instrument accuracy.

1.3.2 2D synchronization correlation spectroscopy

In this study, the static perturbation was the concentration of soil heavy metals. The correlation type was synchronous. The slice of synchronous spectra was taken at 50. The moving window size (2m+1) was 11. The draw type was contour and the counter layer was 8.

The detection limit is defined as three times the standard deviation of the blank test according to the International Union of Pure and Applied Chemistry (IUPAC, 1976). The SiO₂ (analytical purity) sample testing was repeated 11 times, and the instrument detection limits were shown in Table 1. The detection limits of As, Pb, Cr and Zn were 3.95, 5.13, 16.35 and 10.20 mg· kg^-1, respectively. The quantitative detection limit of Cr was the highest and the result indicated that the detection sensitivity of Cr in soil by using this instrument was relatively low. The detection limit values of the four elements were lower than the primary soil standard value in the environmental quality standard for soils of China (GB15618— 1995).

Table 1

Table 1

Table 1 Instrument detection limit (n=11) Elements Detection limit/(mg· kg-1) Pb 5.13 As 3.95 Zn 10.20 Cr 16.35

Table 1 Instrument detection limit (n=11)

The accuracy analysis results were obtained according to the equation:

A(%)=CiCs×100(1)

where A is accuracy, C_i is the content of soil heavy metals by the instrument and C_s is the standard value of soil heavy metals. The units of C_i and C_s are mg· kg^-1. The correlation analyses between the soil heavy metals content by the instrument with the standard values using simple linear regression were shown in Fig.1.

Fig.1

	Figure Option ViewDownloadNew Window
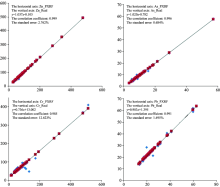	Fig.1 Linear regression between soil heavy metals content by the instrument with the standard values

The accuracies of Zn, Pb, Cr and As were 92%~105%, 70%~120%, 71%~180%, 84%~138%, respectively, according to Eq. 1. The accuracy was the lowest for Cr, although the correlation coefficient was more than 0.98 (Fig.1). The degree of dispersion and standard error for Cr were the largest. The results indicated that the detection sensitivity of Cr in soil using this instrument was relatively low and that the detection sensitivities of Zn, Pb and As in soil were good. Overall, testing heavy metal elements in soil using this instrument was feasible.

Taking GBW07405 (GSS-5) as an example, the main and low range Energy-Counts maps in the low energy spectra were shown in Fig.2. The low-range Energy-Counts map was selected to cover the 0~20 keV energy range because the energy intensities of 20~40 keV were almost 0. The heavy metal types in the different filter plates were different and the counts of heavy metal elements also showed differences. Zn and As were determined using each filter plate, and Cr was determined using low filter plate (Fig.2). K lines of Pb required high energy, but voltage of handheld instrument was not enough to stimulate the signal of high energy intensity. So L lines of Pb were analyzed in the study. Therefore, it is necessary to select the appropriate range of spectral lines to generate a quantitative analysis model of heavy metals.

Fig.2

	Figure Option ViewDownloadNew Window
	Fig.2 Main and low range Energy-Counts maps of GSS-5 in the low energy spectra

To reduce or eliminate the influence of non-target factors, PLSR was applied to the 52 soil standard samples to determine the accuracy of different ranges in the low energy spectra for model prediction. The results were shown in Table 2. The optimal number of regression factors for the PLSR model was determined by the correlation coefficient, R-square, root mean standard error of calibration (RMSEC) and standard error of calibration (SEC) of cross validation. The model performance depends on the comprehensive evaluation of the correlation coefficient, R-square, RMSEC and SEC. The judging standard of the model is that the correlation coefficient is close to 1 and the difference between SEC and RMSEC is the lowest. According to Table 2 and the evaluation standard, the model performance for Pb, As and Zn in the main range was good and the model performance for Cr in the low range was good. The results were consistent with the heavy metal range of the filter plate.

Table 2

Table 2

Table 2 Influence of different range on the precision of the model Elements Range Correlation R-square RMSEC SEC MAIN 0.999 0.998 2.990 3.019 Pb HIGH 0.999 0.998 3.152 3.183 LOW 0.459 0.210 64.870 65.503 MAIN 0.999 0.999 1.049 1.059 As HIGH 0.999 0.999 1.530 1.545 LOW 0.460 0.212 49.399 49.881 MAIN 0.995 0.990 7.959 8.037 Zn HIGH 0.993 0.985 9.921 10.018 LOW 0.973 0.947 18.804 18.987 MAIN 0.834 0.696 40.643 41.039 Cr HIGH 0.775 0.601 46.591 47.045 LOW 0.993 0.987 8.493 8.576 Note: RMSEC is root mean standard error of calibration. SEC is standard error of calibration. The units of SEC and RMSEC are mg· kg-1

Table 2 Influence of different range on the precision of the model

Generally, it is meaningful to reduce the spectra dimension for variable detection. Calibration with the full range of variables is time consuming and irrelevant information within the spectra would affect the accuracy and robustness of the model. To meet the need for rapid detection, variable selection was applied to simplify the models and improve detection efficiency. There are many variable selection methods that have been investigated such as genetic algorithm, uninformative variable elimination and successive projections algorithm. In this paper, 2D synchronization correlation spectroscopy was introduced as a novel variable selection method to determine the variable range for detection of heavy metals using XRF spectroscopy.

Characteristic XRF energy intensities of heavy metal elements were shown in Table 3. Lα and Lβ line intensities of Zn, As and Cr are lower than 1.5 keV, which can be negligible. So Kα and Kβ of Zn, As and Cr were selected as the quantitative spectral line intensities. Kα and Kβ line intensities of Pb are higher than 70 keV. The excitation energy of the NITON XL3t 600 X-ray fluorescence spectrometer is 30 keV. So Kα and Kβ of Pb can be considered negligible and Lα and Lβ of Pb were selected as the quantitative spectral line intensities.The EDXRF Kα and Kβ line intensities were measured for all elements except Pb, for which the Lα and Lβ line intensities were measured.

Table 3

Table 3

Table 3 Characteristic X-ray energy values of elements during X-ray fluorescence analysis Elements Kα Kβ Lα Lβ Pb 74.970 84.939 10.551 12.614 As 10.543 11.726 1.282 1.317 Cr 5.415 5.947 0.572 0.582 Zn 8.637 9.570 1.012 1.035

Table 3 Characteristic X-ray energy values of elements during X-ray fluorescence analysis

To obtain the energy analysis range of heavy metal elements, representative samples of Pb (552, 61, 40, 28 and 14 mg· kg^-1), As (412, 58, 21.7, 10.6 and 6.3 mg· kg^-1), Zn (494, 210, 127, 66 and 22 mg· kg^-1) and Cr (410, 370, 92, 65 and 43 mg· kg^-1) were selected and analyzed using 2D synchronization correlation spectroscopy as a novel qualitative analysis method. The 2D fluorescence contour maps of Pb, Cr, As and Zn were shown in Fig.3 using 2Dshige software according to Kα , Kβ of Zn, As, Cr and Lα , Lβ of Pb. The diffusion range of the correlation coil was used to determine the energy range of quantitative analysis and variable numbers. The results were shown in Table 4.

Fig.3

	Figure Option ViewDownloadNew Window
	Fig.3 Two-dimensional fluorescence contour maps of Pb (a, b), As(c, d), Cr (e, f) and Zn (g, h)

Table 4

Table 4

Table 4 Energy range and variable numbers Elements Contour map Energy/keV Number of variables Auto-cross peak/keV Scale of correlation Pb a 10.380~10.740 25 10.560 222.489 b 12.435~12.900 32 12.630 55.809 As c 10.380~10.740 25 10.560 218.597 d 11.610~11.880 19 11.745 2.334 Cr e 5.310~5.520 15 5.415 17.878 f 5.805~6.015 15 5.895 92.026 Zn g 8.520~8.805 20 8.640 2.165 h 9.555~9.630 6 9.585 0.074

Table 4 Energy range and variable numbers

The auto-correlation peak was very close to Kα , Kβ of Zn, As, Cr and Lα , Lβ of Pb in Fig.3. The contribution rates of Kα (Zn and As), Kβ (Cr) and Lα (Pb) line intensities were the largest from the correlation analysis. The energy resolution was 0.015 keV. In Table 4, the variable numbers of Pb, As, Cr and Zn were 57, 44, 30 and 26, respectively.

The quantitative analysis model of heavy metals was established according to the energy range obtained by 2D synchronization correlation spectroscopy. The 52 standard samples were divided into a calibration set (n=39) and a prediction set (n=13) using the Kennard-Stone algorithm. Multivariate calibration models were built using PLSR and the results were shown in Table 5. The correlation coefficients (R_p) of Pb and As prediction sets were higher than 0.97, R_p of Zn was 0.963 and R_p of Cr was 0.922. The differences between SEP and RMSEP of Pb, As, Zn and Cr elements were 0.040, 0.029, 0.378 and 1.933 mg· kg^-1, respectively. Overall, the prediction performance of Cr was relatively poor. Given spectra within the selected energy range, multivariate calibration models for the heavy metals Pb, As, Cr and Zn can be built to achieve excellent accuracy. The results indicated that the instrument was suitable for the detection of heavy metals Pb, As, Cr and Zn in soil and the principle could be expanded for the determination of other elements.

Table 5

Table 5

Table 5 Statistical parameters of the calibration and prediction set Elements Range Variables PC Rc SEC RMSEC Rp SEP RMSEP Pb MAIN 57 2 0.996 7.795 8.008 0.970 1.458 1.418 As MAIN 44 2 0.997 5.254 5.398 0.972 0.578 0.607 Zn MAIN 26 2 0.969 22.647 23.267 0.963 5.353 5.731 Cr LOW 30 3 0.895 37.670 39.251 0.922 5.321 7.254 Note: PC is principal component, Rc is the correlation coefficient of calibration, SEC is the standard error of calibration, RMSEC is the root standard error of calibration, Rp is the correlation coefficient of prediction, SEP is the standard error of prediction, and RMSEP is the root standard error of prediction. The units of SEC, RMSEC, SEP and RMSEP are mg· kg-1.

Table 5 Statistical parameters of the calibration and prediction set