作者简介: 王英俊, 1991年生, 中国科学院光电研究院硕士研究生 e-mail: wangyingjun15@mails.ucas.ac.cn
为满足机载星载平台对光谱成像系统紧凑型和轻量化的需求, 克服当前光谱成像技术分光系统结构复杂、 成本高的不足, 提出了基于量子点材料的光谱成像技术方案。 将条带状的量子点阵列片放置于前置镜焦面前, 利用量子点材料对光谱的吸收特性对探测目标的入射光谱进行调制, 使用最小二乘法建立探测目标的光谱重建模型, 采用推扫的方式获取数据并进行光谱重建可以获得目标光谱和空间信息。 量子点光谱成像技术具有光谱分辨率高、 能量利用率高、 体积小、 光谱范围宽和成本低等优势。 分析了不同光谱谱段间隔和噪声等因素对重建光谱分辨率的影响, 以及对重建光谱准确性或者失真度的影响。 分析得出谱段间隔越低, 光谱分辨率越高; 重建的准确性和分辨率随着噪声水平的增大而降低; 适当的提高谱段间隔, 可以提高重建的准确性。 将已知数据立方体和它的仿真结果进行对比, 可以看出还原得到的量子点光谱图像质量较好, 验证了该技术的可行性。 量子点材料为光谱成像技术提供了新的途径, 在航空航天等小型化光谱遥感领域具有极大的应用潜力。
In order to meet the requirement of compact type and lightweight for spectral imaging system in airborne and satellite platform, and to overcome the limitations of optical splitting system in current spectral imaging technology such as complex structure and high cost, for the first time we present the design of spectral imaging based on quantum dots. In this method, a strip of quantum dots array is placed in front of the focal plane of telescope lens and absorption properties of quantum dots materials is applied to modulate the incident spectrum of the target, then least square method is applied to establish the spectral reconstruction model of the target. Finally, the spectral and spatial information of the target is obtained with the method of push broom and spectral reconstruction. The quantum dots spectral imaging technology has the advantages of high spectral resolution, high energy availability, small size, wide spectral range and low cost. More important, the effects of different spectral intervals and noises on the reconstructed spectral resolution and their impact on the accuracy or distortion of the reconstructed spectra are analyzed. The results show that the spectral resolution increases with the decrease of the spectral interval, and the accuracy and resolution of the reconstructed spectrum are reduced with the increase of the noise level. What's more, the accuracy of reconstruction can be improved by appropriately increasing the spectral interval. With a comparison of the simulation results with the known data cube, the feasibility of the technology is verified, and the results show that the quantum dots spectral imaging possesses higher quality. In conclusion, quantum dots provide a new approach for spectral imaging technology, which has wide applications in the field of aerospace and other miniature spectral remote sensing.
光谱成像技术是一种将成像和光谱相结合的多维信息获取技术, 能够获得被探测目标的二维空间信息和地物光谱信息, 形成三维数据立方体, 实现对目标特性的综合探测感知与识别[1]。 近年来, 无论是星载还是机载遥感平台, 都要求其有效载荷尽可能的轻量化[2]。 因此, 研制紧凑型轻量化光谱成像仪器已成为光谱遥感技术发展的重点。 传统的光谱成像技术的分光方式主要有棱镜, 光栅和滤光片分光等[3]。 但是棱镜和光栅型都带有复杂的分光元件, 体积庞大、 造价昂贵[4]; 滤光片阵列型或线性渐变滤光片型光谱成像仪[5, 6], 由于镀膜工艺或滤光片本身特性, 使得光谱范围和光谱分辨率受限, 无法满足高光谱成像的应用需求。
量子点(quantum dots, QDs)也称纳米晶[7], 半径接近或小于激子波尔半径, 是近年来发展起来的一种半导体纳米材料, 在光学、 电子学和生物医学等领域都有着广阔的应用前景。 2015年, 美国科学家首次利用量子点材料的吸收特性制作完成的量子点微型光谱仪, 具有高光谱分辨率, 高能量利用率, 体积小和成本低等优势[8], 但无法作为光谱成像仪使用。
基于量子点在光谱测量方面的巨大优势和潜能, 提出将量子点材料应用到光谱成像领域。 将具有不同光谱吸收特性的条带状量子点阵列片放于前置望远镜焦面。 当系统推扫时, 被测物点光谱依次通过所有量子点, 得到一组关于未知量为入射光谱的方程组, 利用最小二乘法建立光谱重建模型, 获得条带状不同物点的光谱数据, 最后将每一行条带的光谱数据进行拼接, 从而得到整个目标物的空间信息和光谱信息。 由于量子点光谱成像技术不需要狭缝和复杂的分光结构, 因此满足了光谱成像仪小型化的需求, 提高了系统能量利用率并降低了系统研发成本, 在军、 民领域, 特别是要求载荷小型化的星载和机载等应用平台具有广阔的应用前景。
本文首先论述了量子点光谱成像的原理。 然后详细的阐述了光谱重建方法。 最后利用已知目标数据立方体进行仿真试验, 并分析噪声等对光谱成像性能的影响。
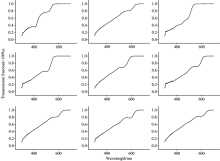
量子点是半径接近或小于激子波尔半径的半导体纳米晶体, 一般情况下是由Ⅱ -Ⅵ 族(CdSe, CdTe和CdS等)、 Ⅲ -Ⅴ 族(InP, InAs)或者Ⅳ -Ⅵ 族、 Ⅴ -Ⅵ 族元素组成。 量子点光学性质表现为, 当其尺寸减小到纳米量级的时候, 使得量子点对不同光谱的吸收能力越来越强; 量子点对光的吸收过程, 还要受到尺寸效应和表面电荷分布的影响。 因其特有的光学性质, 使得量子点成为一种理想的滤光材料。 利用有机高温注射法合成硒化镉(CdSe)量子点[9], 并在后期处理过程中将荧光效应猝灭, 避免影响量子点透过率的测试结果。 通过控制反应条件, 可以制得不同光谱特性的CdSe量子点。 利用紫外-可见分光光度计可以得到量子点透过率曲线, 部分量子点光谱透过率如图1所示。
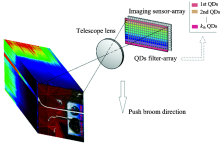
本文基于量子点的吸收光谱特性, 提出了量子点光谱成像系统, 其基本组成包括: 前置望远镜、 量子点阵列片和图像探测器。 量子点阵列片位于前置望远镜的后焦面, 紧靠量子点阵列片放置图像探测器, 如图2所示。 其中量子点阵列片是将具有不同吸收光谱特性的量子点材料沿垂直于推扫方向平行制备在基底上, 每一个条带的量子点材料覆盖一行或多行像元。
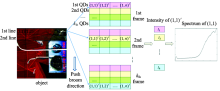
量子点光谱成像系统采用推扫方式获取数据, 如图3所示。 以目标物第一行为例, 第一帧观测时每个物点的光谱经前置镜成像于第一种量子点材料上。 由于量子点阵列与图像探测器紧靠在一起, 所以入射光谱经量子点调制后, 探测器获得相应的光强数据由如式(1)进行表述
式(1)中, T(λ )是量子点关于波长的透过率函数, d(λ )是图像探测器对波长的响应函数, ϕ (λ )是入射光谱, 光谱范围为a~b。
随着光谱成像系统的推扫, 目标物第一行沿推扫方向成像于第二种量子点材料上, 因此第二帧观测时, 在探测器第二行像元上获得目标物第一行经第二种量子点调制后的光强数据。 以此类推, 当推扫结束后, 每一个条带状目标物依次通过量子点阵列上的所有量子点, 得到一组采样数据。
通过建立相应的数学重建模型, 将所得到的光强数据利用合适的算法进行重建, 即可获得每一行不同物点的光谱数据。 将每一行的数据进行图像拼接, 从而得到整个目标景物的空间信息和光谱信息。
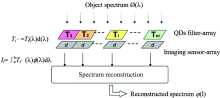
为了准确获得物点的光谱信息, 需要建立相应的数学模型进行光谱重建。 光谱重建的数学模型如图4所示[10]。
任意的入射光谱ϕ (λ ), 通过nF个不同量子点, 由式(1)可得每一种量子点调制后的透射光强Ii为
式中T'i(λ )=Ti(λ )d(λ ), 其中Ti(λ )是不同量子点关于波长的透过率函数, d(λ )是图像探测器对波长的响应函数。
为了获得式(2)的数值解, 我们先将连续的入射光谱分成由nλ 个离散波长组成, 得到式(3)为
式(3)中, 离散波长的光谱谱段间隔为Δ =(b-a)/(nλ -1)和λ j=a+(j-1)× Δ 。 当j=1和nλ 时, Δ λ j=Δ /2; 当j为其他数值时, Δ λ j=Δ 。 在给定波长范围的情况下, 增加离散波长的数量, 可以增加光谱分辨率。
为了能够更好的阐述, 我们将式(3)得到的一组方程写成矩阵形式
式(4)中, ϕ '(λ )=(ϕ (λ 1)Δ λ 1, ϕ (λ 2)Δ λ 2, …, ϕ (λ j)Δ λ j)T, 数据向量I∈ Ri× 1由入射光谱通过量子点后所形成的光强所组成, 数据矩阵T'(λ )∈ Ri× j中每一行表示量子点不同波长的光谱吸收率。 行数i表示我们之前所提到的量子点数量。 未知量ϕ '(λ )∈ Rj× 1, 未知量的行数j代表离散波长数量, j值越多, 光谱分辨率越高。
在理想情况下, 入射光谱的离散波长数量nλ 和量子点数量nF相等, 线性方程组(4)有唯一解。 近似的解决方法可以利用最小二乘线性回归的计算方法获得该入射光谱曲线ϕ (λ )。 在实际测量过程中, 会存在一定的观测误差或噪声, 即I=I0+n, 其中I0和n分别为无误差数据向量和误差向量。 将式(4)加入误差向量可以得到如式(5)。
由于测量误差和系统噪声的存在, 使式(5)的方程组是病态的, 重建之后的光谱与入射光谱相差较大。 为了能够更好的重建光谱, 算法的选取将是决定性的因素。 在此利用最小二乘法[11]得到最优解。
最小二乘法的核心思想是求出的解向量ϕ '(λ )能够使矩阵方程两边的误差平方和最小[12]。 于是矩阵方程T'(λ )ϕ '(λ )=I的普通最小二乘解为
对于超定矩阵的满列秩, 即rank(T'(λ ))=j, 由于T'(λ )TT'(λ )非奇异, 所以方程有唯一解为[12]
令T'(λ )=UΣ VH是矩阵T'(λ )的奇异值分解, 从而得到普通最小二乘解为[12]
在最小二乘法求解过程中, 可以转换为迭代的方法进行求解。 令初始解向量为ϕ '(λ
同样, T'(λ )=UΣ VH是矩阵T'(λ )的奇异值分解, 代入迭代式(9)中可得
利用ϕ '(λ )=(ϕ (λ 1)Δ λ 1, ϕ (λ 2)Δ λ 2, …, ϕ (λ j)Δ λ j)T和求解得到的ϕ '(λ ), 可以得到向量(ϕ (λ 1), ϕ (λ 2), …, ϕ (λ j))T, 即物点的入射光谱ϕ (λ )。
为了验证量子点光谱成像技术的可行性和分析各项因素对其的影响, 将实验室现有的高光谱成像仪获得的地物三维光谱数据立方体作为仿真的入射光谱, 利用建立的数学模型和算法对光谱进行重建。 分析不同光谱谱段间隔和噪声等因素对重建光谱分辨率的影响, 以及对重建光谱准确性或者失真度的影响。
仿真实验中采用了195种量子点, 光谱范围为400~700 nm, 并采用服从正态分布的随机噪声, 利用式(5)得到入射光谱通过量子点所得到的光强数据, 并利用算法进行光谱重建。
光谱分辨率是指光谱成像系统各谱段的带宽, 若光谱分的愈细, 探测的波段愈多, 波段间的间隔愈小, 光谱分辨率愈高[13]。 为了更好的分析重建光谱的分辨率, 分别对不同双峰间隔的入射光谱进行重建, 能够识别的双峰间隔越小, 则光谱分辨率越高[8]。 在光谱分辨率分析的仿真实验中, 入射光谱的峰值光强(最大值)为1。 如图5— 图7表示的是在噪声水平σ =0.000 01[8]的情况下, 不同谱段间隔和双峰间隔的入射光谱与重建光谱。
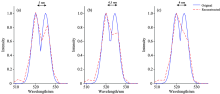 | 图5 光谱谱段间隔3 nm, 双峰间隔分别为5, 4.5 nm和4 nmFig.5 The spectral interval is 3 nm, and the interval between two peaks is 5, 4.5 and 4 nm respectively |
 | 图6 光谱谱段间隔2.5 nm, 双峰间隔分别为4.5, 4和3.5 nmFig.6 The spectral interval is 2.5 nm, and the interval between two peaks is 4.5, 4 and 3.5 nm respectively |
 | 图7 光谱谱段间隔2 nm, 双峰间隔分别为4, 3.5和3 nmFig.7 The spectral interval is 2 nm, and the interval between two peaks is 4, 3.5 and 3 nm respectively |
从图5— 图7的结果来看, 重建光谱的光谱谱段间隔为3 nm、 双峰间隔为5 nm的时候, 能够有效的识别双峰位置; 当双峰间隔为4.5 nm时, 虽然丢失了一些光谱信息, 但依然可以很好地识别; 随着双峰的间隔减小到4 nm时, 已经不能识别出双峰。 因此, 当谱段间隔为3 nm时, 可识别的双峰间隔为4.5 nm。 同样, 重建光谱的谱段间隔为2.5和2 nm时, 可识别的双峰间隔分别为4和3.5 nm。 由此发现, 重建光谱的光谱谱段间隔越小, 可识别的双峰间隔越小, 重建光谱的分辨率越高。 在本文中, 光谱谱段间隔最小值等于光谱范围与量子点数量的比值, 量子点数量越多, 可以获得的光谱谱段间隔越低, 光谱分辨率越高。
如图8为不同噪声水平的光谱重建, 重建光谱的谱段间隔2 nm。 图中(a), (b), (c)和(d)的随机噪声水平分别为0, 0.000 01, 0.000 015和0.000 02[8]。 图8的结果表明, 在噪声水平为0, 重建光谱与入射光谱很好的匹配; 在噪声水平σ =0.000 01, 重建光谱与入射光谱有极小的差别; 随着噪声水平增加到0.000 015, 入射光谱与重建光谱的差异增大, 然而双峰的位置依然能够识别; 当噪声水平增加到0.000 02时, 最后的仿真结果为一个宽谱峰, 无法对双峰位置进行识别, 失去了准确性。 因此, 重建光谱的准确性和分辨率随着噪声水平的增大而降低。
为了分析量子点光谱成像系统对重建目标图像空间信息和光谱信息的有效性和重建光谱的准确性, 采用高光谱成像仪获取目标物的三维数据立方体作为仿真实验中的入射光谱, 谱段间隔为0.5 nm, 空间样本大小为200× 200像素, 入射光谱的峰值强度为2 048坎德拉, 使用最小二乘完成所有像素的光谱重建, 形成重建后的数据立方体, 对其进行光谱分割获得某一波段的单波长图像, 选取特征物分析光谱的准确性和单波长图像的成像质量。
通常采用有效均方误差(mean square error, MSE)来评价重建光谱的准确性, 其表达式为
式(11)中, ϕ (λ j)为计算所得的参数, φ (λ j)为原始的光谱参数。 也可以采用相对光谱二次误差(relative spectral quadratic, RQE)分析特征地物光谱的失真度, 如式(12)所示
式(12)中, φ (λ )为原始数据, ϕ (λ )为重建数据, RQE越大, 失真度越大[14]。
对单波长图像进行误差分析, 最常用的方法是有效均方误差(MSE)和峰值信噪比(peak signal-to-noise ratio, PSNR), 其对应公式如式(13)和式(14)所示
式中M和N分别表示图像的行数和列数, ϕ (λ )ij为通过计算和光谱分离得到的参数, φ (λ )ij为原始的单波长光谱参数, L为图像中光强最大的值。
如图9所示为谱段间隔为2 nm, 噪声水平σ =0.003[8], 图9(a)为图像中特征物红旗上某一点[坐标为(87, 100)]的入射光谱, 图9(b)为重建后图像中同一点的光谱, 图9(c)为光谱分割后598 nm的单波长入射图像, 图9(d)为光谱重建后的单波长图像。 如图10(a)图为原入射光谱的彩色合成图, 图10(b)为重建之后的彩色合成图。 从图中数据发现, 重建后的特征物光谱的MSE为412.906 9, RQE为0.21127%< 1%[15], 重建光谱与入射光谱的差异较低。 重建后单波长图像的MSE为386.824, PSNR为44.751 7。 无论从光谱还原效果还是单波长图像质量来看, 最小二乘法在量子点光谱成像中的还原效果较好, 进一步验证了量子点光谱成像系统的可行性以及重建算法的正确性。
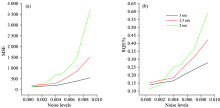
如图11所示为同一特征地物不同噪声水平和不同光谱谱段间隔下光谱的MSE值和RQE值。 观察图中曲线趋势发现: 首先, 相同的光谱谱段间隔下, 噪声水平越低, MSE值越低, RQE越低, 重建光谱的相似度越高, 失真度越低; 其次, 相同噪声情况下, 当重建光谱失真度较低时, 提高光谱谱段间隔可能不会获得更好的效果, 当重建光谱的效果不好时, 适当的提高重建光谱的光谱谱段间隔, 将有效降低MSE值和RQE值, 提升重建光谱的准确性, 增强系统的容噪能力。 提高光谱谱段间隔, 相当于降低T'(λ )的满列秩与矩阵T'(λ )的行数(量子点数量)的比值。 因此, 在相同的光谱谱段间隔下, 适当的提高量子点数量, 同样可以提高重建光谱的准确性, 增强系统的容噪能力。
为满足光谱成像系统低成本小型化的需求, 利用量子点材料对入射光谱的吸收特性, 提出了一种量子点光谱成像的技术方案, 建立了光谱重建数学模型。 讨论了影响重建光谱分辨率和准确性的因素, 得出如下结论: (1)重建光谱的谱段间隔越低, 光谱分辨率越高; (2)重建的准确性和分辨率随着噪声水平的增大而降低; (3)适当的提高重建光谱的谱段间隔, 可以提高重建的准确性。 数据立方体的重建结果表明, 特征物光谱和单波长图像的重建效果较好, 进一步验证了量子点光谱成像技术实现目标光谱和空间信息探测的可行性和正确性。 为实现量子点光谱成像技术的深入研究和实验验证提供了理论基础, 并且在小型化光谱成像领域具有广阔的应用前景。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|